3d вращение вокруг начала координат
Я знаю, что есть много вопросов о 3D-вращении, на которые здесь ответили, но все они, похоже, имеют дело с вращательными матрицами и кватернионами в OpenGL (и мне все равно, если я получу карданный замок). Мне нужно получить 3d-координаты EX: (x,y,z) точки, которая всегда должна быть на одном и том же расстоянии, я назову ее "d" сейчас, от начала координат. Единственная информация, которую я имею в качестве ввода, - это deltax и deltay мыши по экрану. Пока вот что у меня попробовал:
первый:
thetaxz+=(omousex-mouseX)/( width );
thetaxy+=(omousey-mouseY)/( height);
(thetaxy-угол в радианах на оси x, y и thetaxz на оси x, z) (Я ограничиваю оба угла так, что если они меньше или равны 0, они равны 2*PI)
второй:
pointX=cos(thetaxz)*d;
pointY=sin(thetaxy)*d;
(pointX-Координата точки x, а pointY-y)
третий:
if(thetaxz)<PI){
pointZ=sqrt(sq(d)-sq(eyeX/d)-sq(eyeY/d));
}else{
pointZ=-sqrt(abs(sq(d)-sq(eyeX/d)-sq(eyeY/d)));
}
(sq () - это функция, которая квадраты и abs () является функцией абсолютного значения) (pointZ должен быть координатой Z точки и это только при пересечении между положительной оси Z полушарии и отрицательной оси Z полушарии. По мере приближения к краю точка растягивается дальше, чем расстояние, на котором она всегда должна быть в x и y, и, казалось бы, случайным образом вокруг 0,1-0,2 радианов оси Z координата становится NAN или неопределенной)
Я думал об этом некоторое время, и, честно говоря, у меня возникли трудности с искривлением головы вокруг концепции кватернионов и вращательных матриц, однако, если вы может показать мне, как использовать их для генерации фактических координат, которые я был бы рад узнать. Я все равно предпочел бы, чтобы я мог просто использовать тригонометрию в нескольких осях. Спасибо заранее за любую помощь и если вам нужна дополнительная информация, пожалуйста, просто спросите.
подсказка / идея последней минуты: я думаю, что это может иметь какое-то отношение к позиции z, влияющей на позиции x и y, но я не уверен.
EDIT: я нарисовал диаграмму:
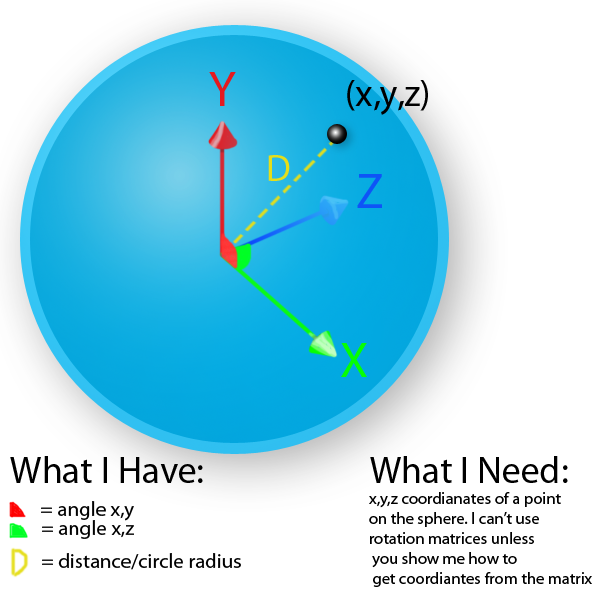
1 ответов
Если вы действительно хотите успеха в этом, вам придется укусить пулю и узнать о вращение матриц и / или кватернион вращения. Могут быть и другие способы сделать то, что вы хотите, но матрицы вращения и кватернионные вращения используются просто потому, что они широко понимаются и являются одним из простейших средств выражения и применения вращений к векторам. Любое другое представление, кто-то может придумать, вероятно, будет более сложным переформулировка одного или обоих из них. На самом деле можно показать, что вращение-это линейное преобразование и поэтому может быть выражена как матрица. Кватернионные вращения - это просто упрощенное средство вращения векторов в 3D и поэтому имеют эквивалентные матричные представления.
тем не менее, похоже, вам интересно захватить объект в вашей сцене щелчком мыши и вращаться естественным образом. Если это так, вы должны смотреть на the ArcBall способ (здесь многочисленные примеры вы можете посмотреть). Это все еще требует, чтобы вы знали что-то о кватернионах. Вы также найдете, что, по крайней мере, минимальное понимание основных аспектов линейная алгебра будет полезно.
обновление: на основе вашей диаграммы и комментариев, которые она содержит, похоже, что все, что вы действительно пытаетесь сделать, это преобразовать Сферических Координатах в Декартовых Координатах. Пока мы согласны с обозначением, это легко. Пусть θ-угол, который вы называете XY, то есть угол между осью X, повернутой вокруг оси Z; это называется азимутальным углом и будет в диапазоне [0, 2π) радианов или [0°, 360°). Пусть φ-угол между плоскостью XY и вашим вектором; это называется углом возвышения и будет находиться в диапазоне [- π/ 2, +π/ 2] или [-90°, +90°] и соответствует углу, который вы называете углом XZ (вращение в плоскости XZ вокруг оси Y). Есть и другие соглашения, поэтому убедитесь, что вы последовательны. Во всяком случае, преобразование просто:
x = d∙cos(φ)∙cos(θ) y = d∙cos(φ)∙sin(θ) z = d∙sin(φ)
