Абсолютная погрешность ODE45 и Рунге-Кутты по сравнению с аналитическим решением

Я был бы признателен, если кто-то может помочь со следующим вопросом. У меня есть следующая ОДА:

dr/dt = 4*exp(0.8*t) - 0.5*r   ,r(0)=2, t[0,1]       (1)

я решил (1) двумя разными способами. Посредством метод Рунге-Кутты (4-й порядок) и с помощью ode45 в Matlab. Я сравнил оба результата с аналитическим решением, которое дано:

r(t) = 4/1.3 (exp(0.8*t) - exp(-0.5*t)) + 2*exp(-0.5*t)

когда я строю абсолютную ошибку каждого метода относительно точного решения, я получаю следующий:

для RK-метода мой код:

h=1/50;                                            
x = 0:h:1;                                        
y = zeros(1,length(x)); 
y(1) = 2;    
F_xy = @(t,r) 4.*exp(0.8*t) - 0.5*r;                   
for i=1:(length(x)-1)                              
    k_1 = F_xy(x(i),y(i));
    k_2 = F_xy(x(i)+0.5*h,y(i)+0.5*h*k_1);
    k_3 = F_xy((x(i)+0.5*h),(y(i)+0.5*h*k_2));
    k_4 = F_xy((x(i)+h),(y(i)+k_3*h));
    y(i+1) = y(i) + (1/6)*(k_1+2*k_2+2*k_3+k_4)*h;  % main equation
end

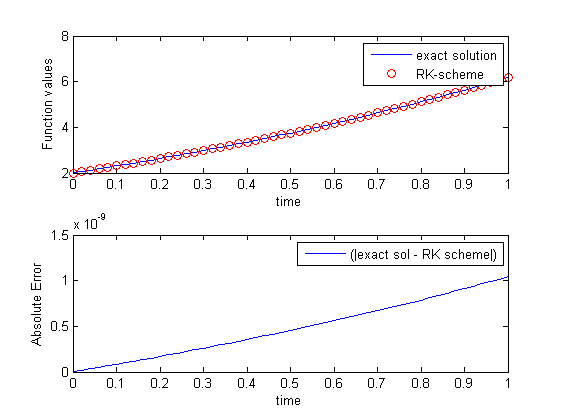
enter image description here

и ode45:

tspan = 0:1/50:1;
x0 = 2;
f = @(t,r) 4.*exp(0.8*t) - 0.5*r;
[tid, y_ode45] = ode45(f,tspan,x0);

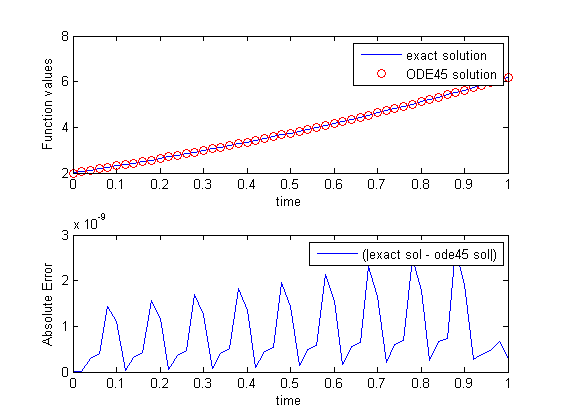
enter image description here

мой вопрос в том, почему у меня есть колебания, когда я использую ode45? (Я имею в виду абсолютную ошибку). Оба решения являются точными (1e-9), но что происходит с ode45 в этом случае?

когда я вычисляю абсолютную ошибку для RK-метода, почему это выглядит лучше?

9
differential-equations matlab numerical-integration ode runge-kutta

2 ответов

ваша функция RK4 принимает фиксированные шаги, которые намного меньше, чем те, которые ode45 идет. То, что вы действительно видите, это ошибка из-за интерполяционного полинома который используется для создания точек между истинными шагами, которые ode45 берет. Это часто называют "плотным выходом" (см. Hairer & Ostermann 1990).

когда вы указываете TSPAN вектор с более чем двумя элементами комплект оду Matlab решатели производят с постоянным шагом выводов. Это не означает, что они фактически используют фиксированный размер шага или используют размеры шага, указанные в вашем TSPAN однако. Вы можете увидеть фактические размеры шага, используемые и по-прежнему получить желаемый фиксированный размер шага, имея ode45 вывод структуры и использование deval:

sol = ode45(f,tspan,x0);
diff(sol.x) % Actual step sizes used
y_ode45 = deval(sol,tspan);

вы увидите, что после первого шага 0.02, потому что ваша ОДА проста она сходится к 0.1 для дальнейшие шаги. Допуски по умолчанию в сочетании с максимальным размером шага по умолчанию (одна десятая интервала интеграции) определяют это. Давайте построим ошибку на истинных шагах:

exactsol = @(t)(4/1.3)*(exp(0.8*t)-exp(-0.5*t))+2*exp(-0.5*t);
abs_err_ode45 = abs(exactsol(tspan)-y_ode45);
abs_err_ode45_true = abs(exactsol(sol.x)-sol.y);
abs_err_rk4 = abs(exactsol(tspan)-y);
figure;
plot(tspan,abs_err_ode45,'b',sol.x,abs_err_ode45_true,'k.',tspan,abs_err_rk4,'r--')
legend('ODE45','ODE45 (True Steps)','RK4',2)

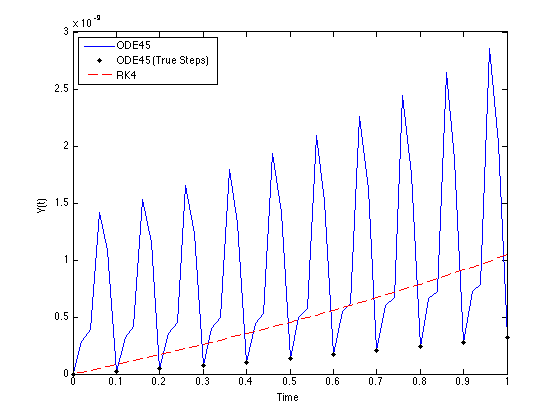
Errors plot

как вы можете видеть, ошибка на истинных шагах растет медленнее, чем ошибка для RK4 (ode45 фактически является методом более высокого порядка, чем RK4, поэтому вы ожидаете этого). Ошибка растет между точками интеграции из-за интерполяции. Если хочешь ... ограничьте это, тогда вы должны отрегулировать допуски или другие варианты через odeset.

если вы хотели заставить ode45 использовать шаг 1/50 вы можете сделать это (работает, потому что ваша ОДА проста):

opts = odeset('MaxStep',1/50,'InitialStep',1/50);
sol = ode45(f,tspan,x0,opts);
diff(sol.x)
y_ode45 = deval(sol,tspan);

для другого эксперимента попробуйте увеличить интервал интеграции для интеграции в t = 10 может быть. Вы увидите много интересного поведения в ошибке (построение относительной ошибки полезно здесь). Вы можете это объяснить? Можете ли вы использовать ode45 и odeset для получения результатов, которые ведут себя хорошо? Интеграция экспоненциальных функций через большие интервалы с адаптивными шаговыми методами является сложной задачей и ode45 не обязательно является лучшим инструментом для работы. Есть варианты однако, но они могут потребовать некоторого программирования.

21

ode45 соединено rk4-rk5. Лично я думаю, что ошибка ODE45 приятнее. Обратите внимание, что он остается ограниченным. Ode4 исправляется, когда величина ошибки становится слишком большой, а минимальная ошибка за цикл составляет около 1e-10. Rk4 "убегает", и ничто его не останавливает.

0