Адаптивный алгоритм порога Брэдли
в настоящее время я работаю над реализацией алгоритма порога под названием Bradley Adaptive Thresholding.
я следовал в основном по двум ссылкам, чтобы выяснить, как реализовать этот алгоритм. Я также успешно смог реализовать два других алгоритма порога, в основном,метод Отсу и Сбалансированная Гистограмма.
вот две ссылки, которые я следовал, чтобы создать Bradley Adaptive Thresholding алгоритм.
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.420.7883&rep=rep1&type=pdf
Пример Адаптивного Порога Брэдли Github
вот раздел моего исходного кода в Python где я запускаю алгоритм и сохраняю изображение. Я использую Python Imaging Library и никаких других инструментов для достижения того, что я хочу сделать.
def get_bradley_binary(inp_im):
w, h = inp_im.size
s, t = (w / 8, 0.15)
int_im = Image.new('L', (w, h))
out_im = Image.new('L', (w, h))
for i in range(w):
summ = 0
for j in range(h):
index = j * w + i
summ += get_pixel_offs(inp_im, index)
if i == 0:
set_pixel_offs(int_im, index, summ)
else:
temp = get_pixel_offs(int_im, index - 1) + summ
set_pixel_offs(int_im, index, temp)
for i in range(w):
for j in range(h):
index = j * w + i
x1,x2,y1,y2 = (i-s/2, i+s/2, j-s/2, j+s/2)
x1 = 0 if x1 < 0 else x1
x2 = w - 1 if x2 >= w else x2
y1 = 0 if y1 < 0 else y1
y2 = h - 1 if y2 >= h else y2
count = (x2 - x1) * (y2 - y1)
a1 = get_pixel_offs(int_im, y2 * w + x2)
a2 = get_pixel_offs(int_im, y1 * w + x2)
a3 = get_pixel_offs(int_im, y2 * w + x1)
a4 = get_pixel_offs(int_im, y1 * w + x1)
summ = a1 - a2 - a3 + a4
temp = get_pixel_offs(inp_im, index)
if temp * count < summ * (1.0 - t):
set_pixel_offs(out_im, index, 0)
else:
set_pixel_offs(out_im, index, 255)
return out_im
вот часть моего кода, который иллюстрирует реализацию эти set и Get методы, которые вы раньше не видели.
def get_offs(image, x, y):
return y * image.size[0] + x
def get_xy(image, offs):
return (offs % image.size[0], int(offs / image.size[0]))
def set_pixel_xy(image, x, y, data):
image.load()[x, y] = data
def set_pixel_offs(image, offs, data):
x, y = get_xy(image, offs)
image.load()[x, y] = data
def get_pixel_offs(image, offs):
return image.getdata()[offs]
def get_pixel_xy(image, x, y):
return image.getdata()[get_offs(image, x, y)]
и, наконец, вот входные и выходные изображения. Это те же изображения, которые используются в оригинальной исследовательской работе в первой ссылке, которую я вам предоставил. Примечание: выходное изображение почти полностью белое, и это может быть трудно увидеть, но я предоставил его в любом случае, если кто-то действительно хотел иметь его для справки.


2 ответов
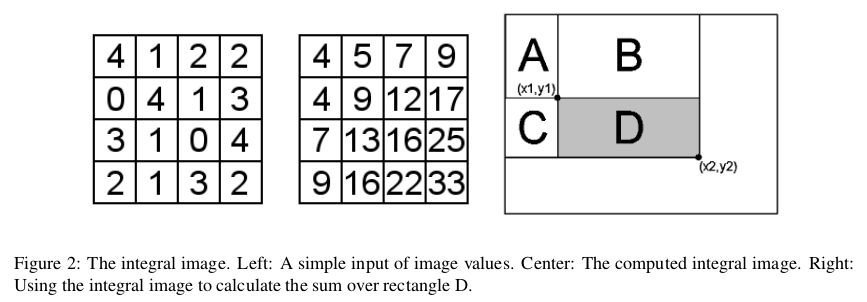
вы не можете создать интегральное изображение с PIL так, как вы это делаете, потому что изображение, в которое вы упаковываете данные, не может принимать значения более 255. Значения в интегральном изображении становятся очень большими, потому что они представляют собой суммы пикселей выше и слева (см. стр. 3 вашей белой книги ниже).
Они будут расти намного больше, чем 255, поэтому нужно 32 бита на пиксель для их хранения.
Вы можете проверить это создав изображение PIL в режиме "L", а затем установив пиксель на 1000000 или некоторое большое число. Затем, когда вы прочитаете значение, оно вернет 255.
>>> from PIL import Image
>>> img = Image.new('L', (100,100))
>>> img.putpixel((0,0), 100000)
>>> print list(img.getdata())[0]
255
EDIT: после прочтения документации PIL вы можете использовать PIL, если создадите свое интегральное изображение в режиме" I "вместо" L". Это должно обеспечить 32 бита на пиксель.
по этой причине я рекомендую Numpy вместо PIL.
Ниже приведена перезапись вашей пороговой функции с помощью Numpy вместо PIL, и я получаю правильный / ожидаемый результат. Обратите внимание, что я создаю свой интегральный образ с помощью массива uint32. Я использовал тот же самый пример C на Github, который вы использовали для своего перевода:
import numpy as np
def adaptive_thresh(input_img):
h, w = input_img.shape
S = w/8
s2 = S/2
T = 15.0
#integral img
int_img = np.zeros_like(input_img, dtype=np.uint32)
for col in range(w):
for row in range(h):
int_img[row,col] = input_img[0:row,0:col].sum()
#output img
out_img = np.zeros_like(input_img)
for col in range(w):
for row in range(h):
#SxS region
y0 = max(row-s2, 0)
y1 = min(row+s2, h-1)
x0 = max(col-s2, 0)
x1 = min(col+s2, w-1)
count = (y1-y0)*(x1-x0)
sum_ = int_img[y1, x1]-int_img[y0, x1]-int_img[y1, x0]+int_img[y0, x0]
if input_img[row, col]*count < sum_*(100.-T)/100.:
out_img[row,col] = 0
else:
out_img[row,col] = 255
return out_img

Я попытался повторно реализовать алгоритм, но без использования массива 1D и переключения на массив 2D numpy, чтобы лучше пойти с оригинальным алгоритмом, упомянутым в фактической статье. Im использует это для исследования анализа данных с использованием моделей глубокого обучения. Это реализация:
import numpy, gc
from ctypes import *
def adaptive_threshold(self):
gc.collect()
gc.disable()
w, h = self._image.width, self._image.height
s, t = w//8, 0.15
summ = c_uint32(0)
count = c_uint32(0)
pixels = self._pixels
int_img = numpy.ndarray(shape=(w, h), dtype=c_int64)
for i in range(w):
summ.value = 0
for j in range(h):
summ.value += sum(pixels[i, j])
if i != 0:
int_img[i, j] = int_img[i - 1, j] + summ.value
else:
int_img[i, j] = summ.value
x1, x2, y1, y2 = c_uint16(0), c_uint16(0), c_uint16(0), c_uint16(0)
for i in range(w):
for j in range(h):
x1.value = max(i - s // 2, 0)
x2.value = min(i + s // 2, h - 1)
y1.value = max(j - s // 2, 0)
y2.value = min(j + s // 2, h - 1)
count.value = (x2.value - x1.value) * (y2.value - y1.value)
summ.value = int_img[x2.value][y2.value] - int_img[x1.value][y2.value] - \
int_img[x2.value][y1.value] + int_img[x1.value][y1.value]
if sum(pixels[i, j]) * count.value < summ.value * (1.0 - t):
pixels[i, j] = 0, 0, 0
else:
pixels[i, j] = 255, 255, 255
gc.enable()
обратите внимание, что это часть класса. Он в основном имеет две переменные: _image, который указывает на фактическое изображение, и _pixels, который является классом PixelAccess, который позволяет получить доступ к пикселям в качестве заданных значений. Я используется деление пола ( / / ) вместо обычного деления ( / ), поскольку оно гарантирует, что все значения целочисленны. Пока результаты выглядят хорошо. Я использовал типы данных C для управления использованием памяти и сохранения значений в фиксированных положениях. Насколько я понимаю, это помогает контролировать небольшое количество данных для минимизации фрагментированных данных.
плюс это последний квартал 2018 года. Люди по-прежнему используют PIL, и, честно говоря, пока это делает свою работу. Это отлично подходит для цветового пространства RGB. Если вы используете это на общих изображениях вы можете преобразовать данные изображения в пространство RGB с помощью:
Image.convert('RGB')
где "Image" является экземпляром open image
это занимает пару секунд на изображениях, которые считаются HD, как 1200x700 изображений, но это заняло несколько долей секунды на образце изображения. Результате Изображения
надеюсь, это кому-то поможет.