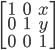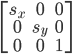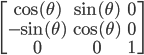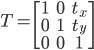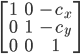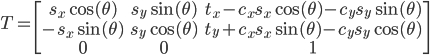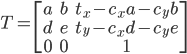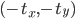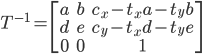Аффинное преобразование Python/PIL
это основной вопрос преобразования в PIL. Я пробовал хотя бы пару раз в последние несколько лет реализовать это правильно и, похоже, есть что-то я не совсем понимаю насчет имиджа.преобразование в PIL. Я хочу реализовать преобразование подобия (или аффинное преобразование), где я могу четко сформулируйте границы изображения. Чтобы убедиться, что мой подход работает я реализовано в Matlab.
реализация Matlab является следующий:
im = imread('test.jpg');
y = size(im,1);
x = size(im,2);
angle = 45*3.14/180.0;
xextremes = [rot_x(angle,0,0),rot_x(angle,0,y-1),rot_x(angle,x-1,0),rot_x(angle,x-1,y-1)];
yextremes = [rot_y(angle,0,0),rot_y(angle,0,y-1),rot_y(angle,x-1,0),rot_y(angle,x-1,y-1)];
m = [cos(angle) sin(angle) -min(xextremes); -sin(angle) cos(angle) -min(yextremes); 0 0 1];
tform = maketform('affine',m')
round( [max(xextremes)-min(xextremes), max(yextremes)-min(yextremes)])
im = imtransform(im,tform,'bilinear','Size',round([max(xextremes)-min(xextremes), max(yextremes)-min(yextremes)]));
imwrite(im,'output.jpg');
function y = rot_x(angle,ptx,pty),
y = cos(angle)*ptx + sin(angle)*pty
function y = rot_y(angle,ptx,pty),
y = -sin(angle)*ptx + cos(angle)*pty
это работает, как ожидалось. Это входные данные:

и это выход:

Это код Python/PIL, который реализует то же самое трансформация:
import Image
import math
def rot_x(angle,ptx,pty):
return math.cos(angle)*ptx + math.sin(angle)*pty
def rot_y(angle,ptx,pty):
return -math.sin(angle)*ptx + math.cos(angle)*pty
angle = math.radians(45)
im = Image.open('test.jpg')
(x,y) = im.size
xextremes = [rot_x(angle,0,0),rot_x(angle,0,y-1),rot_x(angle,x-1,0),rot_x(angle,x-1,y-1)]
yextremes = [rot_y(angle,0,0),rot_y(angle,0,y-1),rot_y(angle,x-1,0),rot_y(angle,x-1,y-1)]
mnx = min(xextremes)
mxx = max(xextremes)
mny = min(yextremes)
mxy = max(yextremes)
im = im.transform((int(round(mxx-mnx)),int(round((mxy-mny)))),Image.AFFINE,(math.cos(angle),math.sin(angle),-mnx,-math.sin(angle),math.cos(angle),-mny),resample=Image.BILINEAR)
im.save('outputpython.jpg')
и это вывод из Python:

Я пробовал это с несколькими версиями Python и PIL на нескольких ОС на протяжении многих лет, и результаты всегда в основном тот же.
Это самый простой случай, который иллюстрирует проблему, я понимаю, что если бы это было вращение, которое я хотел, я мог бы сделать вращение с im.поворот вызова, но я хочу сдвигать и масштабировать тоже, это просто пример, чтобы проиллюстрировать проблему. Я хотел бы получить тот же результат для всех аффинных преобразований. Я бы хотел, чтобы все было правильно.
EDIT:
Если я изменю строку преобразования на это:
im = im.transform((int(round(mxx-mnx)),int(round((mxy-mny)))),Image.AFFINE,(math.cos(angle),math.sin(angle),0,-math.sin(angle),math.cos(angle),0),resample=Image.BILINEAR)
это результат, который я получаю:

EDIT #2
Я повернул на -45 градусов и изменил смещение на -0.5 * mnx и -0.5*mny и получил следующее:

3 ответов
OK! Поэтому я работал над пониманием этого все выходные, и я думаю, что у меня есть ответ, который меня удовлетворяет. Спасибо всем за ваши комментарии и предложения!
Я начинаю, глядя на это:
аффинное преобразование в PIL python?
пока я вижу, что автор может делать произвольные преобразования подобия не объясняет, почему мой код не работал, и не объясняет пространственное макет изображения, которое нам нужно преобразовать он обеспечит линейное алгебраическое решение моих проблем.
но я вижу из его кода, я вижу, что он делит часть вращения матрица (a,b, d и e) в шкале, которая показалась мне странной. Я вернулся к чтению. документация PIL, которую я цитирую:
" im.transform (размер, АФФИН, Данные, Фильтр) => image
применяет аффинное преобразование к изображению и помещает результат в новое изображение с заданным размером.
Data - это 6-кортеж (a, b, c, d, e, f), которые содержат первые две строки из аффинная матрица преобразования. Для каждого пикселя (x, y) в выходном изображении значение берется из позиции (a x + b y + c, d x + e y + f) на входе изображение, округленное до ближайшего пикселя.
эта функция может использоваться для масштабирования, перевода, поворота и сдвига оригинала изображение."
таким образом, параметры (a,b,c,d,e,f) являются преобразование матрицы, но карты (x, y) в целевом изображении до (A x + b y + c, d x + e y + f) в источнике изображение. Но не параметры преобразование матрицы вы хотите подать заявку, но ее обратная. То есть:
- странно
- отличается от Matlab
- но теперь, к счастью, полностью понимает меня
я прикрепляю свой код:
import Image
import math
from numpy import matrix
from numpy import linalg
def rot_x(angle,ptx,pty):
return math.cos(angle)*ptx + math.sin(angle)*pty
def rot_y(angle,ptx,pty):
return -math.sin(angle)*ptx + math.cos(angle)*pty
angle = math.radians(45)
im = Image.open('test.jpg')
(x,y) = im.size
xextremes = [rot_x(angle,0,0),rot_x(angle,0,y-1),rot_x(angle,x-1,0),rot_x(angle,x-1,y-1)]
yextremes = [rot_y(angle,0,0),rot_y(angle,0,y-1),rot_y(angle,x-1,0),rot_y(angle,x-1,y-1)]
mnx = min(xextremes)
mxx = max(xextremes)
mny = min(yextremes)
mxy = max(yextremes)
print mnx,mny
T = matrix([[math.cos(angle),math.sin(angle),-mnx],[-math.sin(angle),math.cos(angle),-mny],[0,0,1]])
Tinv = linalg.inv(T);
print Tinv
Tinvtuple = (Tinv[0,0],Tinv[0,1], Tinv[0,2], Tinv[1,0],Tinv[1,1],Tinv[1,2])
print Tinvtuple
im = im.transform((int(round(mxx-mnx)),int(round((mxy-mny)))),Image.AFFINE,Tinvtuple,resample=Image.BILINEAR)
im.save('outputpython2.jpg')
и вывод из python:

позвольте мне еще раз ответ на этот вопрос в итоговое резюме:
PIL требует обратного аффинного преобразования, которое вы хотите применить.
Я хотел немного расширить ответы на carlosdc и Ruediger Jungbeck, чтобы представить более практичное решение кода python с небольшим объяснением.
во-первых, абсолютно верно, что PIL использует обратные аффинные преобразования, как указано в ответ carlosdc. Однако нет необходимости использовать линейную алгебру для вычисления обратного преобразования из исходного преобразования-вместо этого его можно легко выразить напрямую. Я буду использовать масштабирование и поворот изображения вокруг его центра для примера, как в код связан с на ответ Рюдигера Юнгбека, но довольно просто расширить это, чтобы сделать, например, стрижку.
прежде чем приступить к выражению обратного аффинного преобразования для масштабирования и вращения, рассмотрим, как мы найдем исходное преобразование. Как намекал в ответ Рюдигера Юнгбека преобразование в сочетании операция масштабирования и вращения находится как в составе основных операторов масштабирование изображения о происхождении и поворот изображения о происхождении.
однако, поскольку мы хотим масштабировать и вращать изображение вокруг собственного центра, а начало координат (0, 0) -определяется PIL, чтобы быть верхний левый угол изображения, нам сначала нужно перевести изображение так, чтобы его центр совпадал с началом координат. После применения масштабирование и вращение, нам также нужно перевести изображение обратно таким образом, чтобы новый центр изображения (он может не совпадать со старым центром после масштабирования и вращения) оказался в центре холста изображения.
таким образом, исходное" стандартное " аффинное преобразование, которое мы ищем, будет состоять из следующих фундаментальных операторов:
найти текущий центр
изображения, и перевести изображение
, так центр изображения находится в начале
.
масштабирование изображения о происхождении по некоторому масштабному коэффициенту
.
повернуть изображение о происхождении некоторым углом
.
найти новый центр
изображения, и перевести изображение
таким образом, новый центр окажется в центре холста изображения.
найти преобразование нам, сначала нам нужно знать матрицы преобразований фундаментальных операторов, которые заключаются в следующем:
- перевод
:
- масштабирование с помощью
:
- поворот на
:
тогда наше составное преобразование может быть выражено как:
что равно к
или
здесь
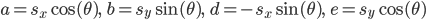
теперь, чтобы найти обратное этому составному аффинному преобразованию, нам просто нужно вычислить состав обратного каждого фундаментального оператора в обратном порядке. То есть, мы хотим
перевести изображение
Поверните изображение относительно начала координат на
.
масштаб изображения о происхождении на
.
перевести изображение
.
Это приводит к матрице преобразования
здесь
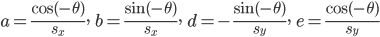
Это точно так же как преобразование, используемое в код связан с на ответ Рюдигера Юнгбека. Оно может сделать более удобным, повторно используя ту же технику, которую carlosdc использовал в своем посте для расчета 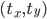
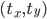
вот переписанная версия кода carlosdc, которая была изменена для использования обратного аффинного преобразования напрямую, а также добавляет масштабирование:
from PIL import Image
import math
def scale_and_rotate_image(im, sx, sy, deg_ccw):
im_orig = im
im = Image.new('RGBA', im_orig.size, (255, 255, 255, 255))
im.paste(im_orig)
w, h = im.size
angle = math.radians(-deg_ccw)
cos_theta = math.cos(angle)
sin_theta = math.sin(angle)
scaled_w, scaled_h = w * sx, h * sy
new_w = int(math.ceil(math.fabs(cos_theta * scaled_w) + math.fabs(sin_theta * scaled_h)))
new_h = int(math.ceil(math.fabs(sin_theta * scaled_w) + math.fabs(cos_theta * scaled_h)))
cx = w / 2.
cy = h / 2.
tx = new_w / 2.
ty = new_h / 2.
a = cos_theta / sx
b = sin_theta / sx
c = cx - tx * a - ty * b
d = -sin_theta / sy
e = cos_theta / sy
f = cy - tx * d - ty * e
return im.transform(
(new_w, new_h),
Image.AFFINE,
(a, b, c, d, e, f),
resample=Image.BILINEAR
)
im = Image.open('test.jpg')
im = scale_and_rotate_image(im, 0.8, 1.2, 10)
im.save('outputpython.png')
и вот как выглядит результат (масштабируется с помощью (sx, sy) = (0.8, 1.2) и поворачивается на 10 градусов против часовой стрелки):
Я думаю этой должны ответить на ваш вопрос.
Если нет, вы должны учитывать, что аффинные преобразования могут быть объединены в другое преобразование.
таким образом, вы можете разделить желаемую операцию на:
перемещение оргина в центр изображения
поворот
перемещение источника назад!--3-->
изменение размера
вы могли бы вычислить одно преобразование из этого.