AI движения космического корабля: посадка 3D-корабля в положение=0 и угол=0
это очень сложная проблема о том, как маневрировать космическим кораблем, который может как переводить, так и вращать в 3D, для космической игры.
космический корабль n двигатели устанавливая в различных положениях и направлениях.
трансформация i - Я струя относительно см космического корабля постоянна = Ti.
- трансформация кортеж положения и ориентации (кватернион или матрица 3x3 или, меньше предпочтительно, углы Эйлера).
- преобразование также может быть обозначено одной матрицей 4x4.
другими словами, вся струя приклеена к кораблю и не может вращаться.
струя может оказывать силу на космический корабль только в направлении его оси (зеленый).
В результате клея ось вращалась вместе с космическим кораблем.
все струи могут оказывать силу (вектор,Fi) на a некоторая величина (скалярная,fi):i - й самолет может оказывать силу (Fi= axis x fi) только в пределах диапазона min_i<= fi <=max_i.
Оба!--10--> и max_i являются постоянными с известным значением.
для ясности, единица min_i,fi,max_i - Ньютон.
Ex. если диапазон не покрывает 0, это означает, что струя не может быть выключена.
m и тензора инерции = I.Этот текущее преобразование космического корабля =
Tran0 скорость = V0, angularVelocity = W0.
физическое тело космического корабля следует известным физическим правилам: -Torque=r x FF=maangularAcceleration = I^-1 x TorquelinearAcceleration = m^-1 x F
I различно для каждого направления, но для простоты, оно имеет такое же значение для каждого направления (сфероподобного). Таким образом, I можно рассматривать как скаляр, а не матрицы 3х3.
вопрос
как управлять всеми струями (all fi) посадить корабль с положением=0 и углом=0?
математические технические характеристики: найти функцию fi(time) это займет минимальное время, чтобы достичь position=(0,0,0), orient=identity С окончательной angularVelocity и velocity = ноль.
более конкретно, каковы имена методов или связанных алгоритмов для решения этой проблемы?
мои исследования (1 dimension)
если Вселенная 1D (таким образом, без вращения), проблема будет легко решить.
(Спасибо Гэвин Замок, https://stackoverflow.com/a/40359322/3577745 )
сначала найдите значение MIN_BURN=sum{min_i}/m и MAX_BURN=sum{max_i}/m.
во-вторых, думайте противоположным образом, предположим, что x=0 (должность) и v=0 at t=0,
затем создайте две параболы с x''=MIN_BURN и x''=MAX_BURN.
(2-е производная считается постоянной в течение определенного периода времени, поэтому она является параболой.)
единственная оставшаяся работа-соединить две параболы вместе.
Красная черта-это место, где они соединяются.
в период времени x''=MAX_BURN, все fi=max_i.
В период времени x''=MIN_BURN, все fi=min_i.
она работает очень хорошо для 1D, но в 3D, проблема гораздо больше посильнее.
Примечание:
Просто грубое руководство, указывающее мне на правильное направление, действительно ценится.
Мне не нужен идеальный ИИ, например, это может занять немного больше времени, чем оптимальная.
Я думаю об этом более 1 недели, все еще не нахожу подсказки.
другие попытки / мнения
- я не думаю, что машинное обучение, такое как нейронная сеть, подходит для этого случай.
- оптимизация с ограничением границ наименьших квадратов может быть полезна, но я не знаю, как подогнать мои две гиперпараболы к этой форме проблемы.
- это можно решить с помощью многих итераций, но как?
- я искал веб-сайт НАСА, но не нашел ничего полезного.
- функция может существовать в игре "космический инженер".
- прокомментировал Logman: знание в механическом инженерия может помочь.
- прокомментировал AndyG: это проблема планирования движения с неголономными связями. Это может быть решено быстрое изучение случайного дерева (RRTs), теория уравнения Ляпунова и линейно-квадратичный регулятор.
- прокомментировал Джон Коулман: это больше похоже оптимальное управление чем AI.
Edit: "near-0 assumption" (необязательно)
- In большинство случай, AI (быть конструированным) бежит непрерывно (т. е. вызванный каждый time-step).
- таким образом, с настройкой ИИ,
Tran0и обычно рядом-личность,V0иW0are обычно не так сильно отличается от 0, например|Seta0|<30 degree,|W0|<5 degree per time-step. - я думаю, что AI, основанный на этом предположении, будет работать нормально в большинство случае. Хотя и не идеальный, его можно рассматривать как правильное решение (я начал думать, что без этого предположения, этот вопрос может быть слишком сложно).
- я слабо чувствую, что это предположение может включить некоторые трюки, которые используют некоторое "линейное"-приближение.
второй альтернативный вопрос - " настройка 12 переменных" (легче)
вышеуказанный вопрос можно также рассматривать следующим образом: -
я хочу настроить все шесть values шесть values' (1-я производная) равняется 0, используя наименьшее количество временных шагов.
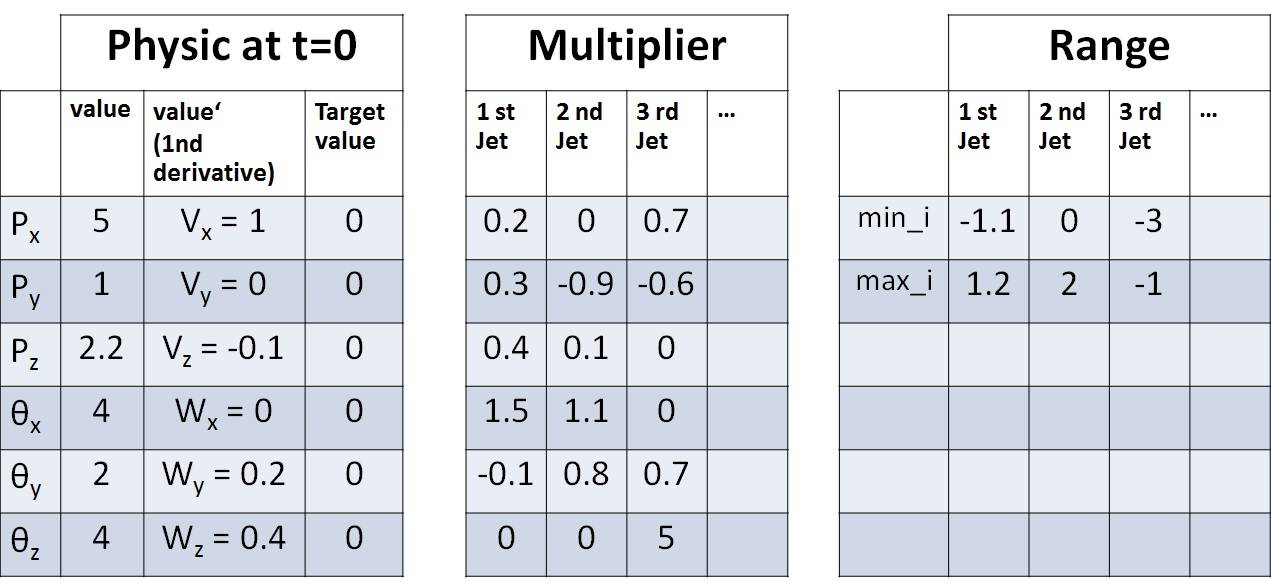
Вот таблица, показывающая возможную ситуацию, с которой может столкнуться AI: -
на множитель стол магазинах inertia^-1 * r и mass^-1 от оригинала вопрос.
на множитель и ряд являются постоянными.
каждый шаг, AI будет предложено выбрать кортеж значений fi что должно быть в диапазоне [min_i,max_i] для каждого i+1-ой самолет.
Ex. из таблицы AI может выбрать (f0=1,f1=0.1,f2=-1).
тогда абонент будет использовать fi умножить на множитель стол получить values''.Px'' = f0*0.2+f1*0.0+f2*0.7Py'' = f0*0.3-f1*0.9-f2*0.6Pz'' = ....................SetaX''= ....................SetaY''= ....................SetaZ''= f0*0.0+f1*0.0+f2*5.0
после этого вызывающий будет обновлять все values' с формулой values' += values''.Px' += Px''.................SetaZ' += SetaZ''
наконец, вызывающий будет обновлять все values с формулой values += values'.Px += Px'.................SetaZ += SetaZ'
AI будет предложено только один раз для каждого шага времени.
цель ИИ возвращать кортежи fi (может отличаться для разных временных шагов), чтобы сделать Px,Py,Pz,SetaX,SetaY,SetaZ,Px',Py',Pz',SetaX',SetaY',SetaZ' = 0 (или очень близко),
используя как можно меньше временных шагов.
я надеюсь, что предоставление другого взгляда на проблему облегчит его.
Это не та же самая проблема, но я чувствую, что решение, которое может решить эта версия может приблизить меня к ответу на первоначальный вопрос.
ответа на этот альтернативный вопрос может быть очень полезным.
3-й альтернативный вопрос - "настройка 6 переменных" (самый простой)
это упрощенная версия с потерями предыдущей альтернативы.
единственная разница в том, что мир теперь 2D,Fi также 2D (x, y).
таким образом, я должен настроить только Px,Py,SetaZ,Px',Py',SetaZ'=0, используя наименьшее количество временных шагов, как это возможно.
ответ на этот самый простой альтернативный вопрос можно считать полезным.
4 ответов
я постараюсь, чтобы это было коротким и сладким.
один подход, который часто используется для решения этих проблем в моделировании, - это Быстро-Изучение Случайного Дерева. Чтобы придать хотя бы немного доверия моей должности, я признаю, что изучал их, и планирование движения было областью моей исследовательской лаборатории (вероятностное планирование движения).
каноническая статья для чтения на них-Стивена Лавалля быстрое изучение случайных деревьев: новый инструмент для пути планирование, и с тех пор было опубликовано миллион статей, которые каким-то образом улучшают его.
сначала я рассмотрю самое основное описание RRT, а затем я опишу, как он меняется, когда у вас есть динамические ограничения. Я оставлю возиться с ним потом до вас:
терминология
"пробелы"
состояние вашего космического корабля может быть описано его 3-мерным положением (x, y, z) и его 3-мерным вращением (Альфа, Бета, Гамма) (я использую эти греческие имена, потому что это углы Эйлера).
состояние пространства все возможные положения и вращения ваш космический корабль может обитать. Конечно, это бесконечно.
место столкновения все "неправильные" государства. то есть реально невозможные позиции. Это состояния, в которых ваш космический корабль сталкивается с каким-либо препятствием (с другими телами это также будет включать столкновение с сам, например, планируя длину цепочки). Сокращенно-c-пространство.
свободное место - это все, что не космические столкновения.
общий подход (без ограничений динамике)
для тела без динамических ограничений подход довольно прост:
- пример состояния
- найти ближайших соседей к этому состоянию
- попытка спланировать маршрут между соседями и государство
я кратко расскажу о каждом шаге
выборка состояния
выборка состояния в самом основном случае означает выбор случайных значений для каждой записи в пространстве состояний. Если бы мы сделали это с вашим космическим кораблем, мы бы произвольно отбирали для x, y, z, alpha, beta, gamma все их возможные значения (равномерная случайная выборка).
конечно, путь больше вашего пространства-это пространство препятствий, чем свободное пространство обычно (потому что вы обычно ограничьте рассматриваемый объект некоторой "средой", в которой вы хотите перемещаться). Поэтому очень часто приходится брать ограничивающий куб вашей среды и пробовать позиции внутри него (x, y, z), и теперь у нас намного больше шансов пробовать в свободном пространстве.
в RRT, вы будете выборочнобольшинство времени. Но с некоторой вероятностью вы действительно выберете свой следующий образец, чтобы быть вашим целевым состоянием (играйте с ним, начните с 0.05). Это потому что вам нужно периодически проверять, доступен ли путь от начала до цели.
поиск ближайших соседей к выборочному состоянию
вы выбрали некоторое фиксированное целое число > 0. Назовем это целое число k. Ваш k ближайшие соседи находятся рядом в пространстве состояний. Это означает, что у вас есть расстояние метрических это может сказать вам, как далеко государства друг от друга. Самая основная метрика расстояния -Евклидово расстояние, который только учитывает физическое расстояние и не заботится об углах поворота (потому что в простейшем случае вы можете повернуть 360 градусов за один шаг).
первоначально у вас будет только начальная позиция, поэтому она будет единственным кандидатом в списке ближайших соседей.
планирование маршрута между государствами
Это называется планирование. В реальном сценарии вы знаете, куда идете, а по пути вам нужно уклоняться от других люди и движущиеся предметы. Мы не будем беспокоиться о таких вещах здесь. В нашем мире планирования мы предполагаем, что Вселенная статична, но для нас.
наиболее распространенным является предположение о некоторой линейной интерполяции между выборочным состоянием и его ближайшим соседом. Сосед (т. е. узел уже в дереве) перемещается вдоль этой линейной интерполяции бит за битом, пока он либо не достигнет выборочной конфигурации, либо не переместится на некоторый максимум расстояние (вспомните метрику расстояния).
то, что здесь происходит, это ваше дерево растет к образцу. Когда я говорю, что вы шаг за шагом "бит за битом", я имею в виду, что вы определяете некоторую" дельту " (действительно небольшое значение) и двигаетесь вдоль линейной интерполяции, что каждый timestep. В каждой точке вы проверяете, если вы новое состояние находится в столкновении с каким-либо препятствием. Если вы попали в препятствие, вы сохраняете последнюю допустимую конфигурацию как часть дерева (не забудьте сохранить край каким-то образом!) Так что вам нужно для местного планировщика:
- проверка столкновения
- как "интерполяция" между двумя государствами (для вашей задачи вам не нужно беспокоиться об этом, потому что мы сделаем что-то другое).
- моделирование физики для timestepping (интеграция Эйлера довольно распространен, но менее стабилен, чем что-то вроде Рунге-Кутта. К счастью у вас уже есть физика модель!
модификация для динамических ограничений
конечно, если мы предположим, что вы можете линейно интерполировать между состояниями, мы нарушим физику, которую вы определили для своего космического корабля. Поэтому мы модифицируем RRT следующим образом:
- вместо выборки случайных состояний мы выберем random управления и управления на определенный срок (или до столкновения).
раньше, когда мы пробовали случайные состояния, на самом деле мы выбирали направление (в пространстве состояний) для движения. Теперь, когда у нас есть ограничения, мы произвольно выбираем элементы управления, что фактически одно и то же, за исключением того, что мы гарантированно не нарушаем наши ограничения.
после применения элемента управления в течение фиксированного интервала времени (или до столкновения) вы добавляете узел в дерево с элементом управления, хранящимся на краю. Ваше дерево будет расти очень быстро, чтобы исследовать пространство. Это приложение управления заменяет линейную интерполяцию между состояниями дерева и состояниями выборки.
выборка элементов управления
вы n двигатели которые индивидуально имеют некоторую минимальную и максимальную силу они могут приложить. Образец в пределах этой минимальной и максимальной силы для каждого двигателя.
к какому узлу(узлам) я применяю свои элементы управления?
Ну, вы можете выбрать наугад, или ваш может смещать выбор, чтобы выбрать узлы, которые ближе всего к вашему состоянию цели (нужна метрика расстояния). Это смещение будет пытаться со временем узлы становятся ближе к цели.
сейчас, с таким подходом, вы вряд ли ровно достичь своей цели, поэтому вам нужно определить некоторое определение "достаточно близко". То есть, вы будете использовать метрику расстояния, чтобы найти ближайших соседей к вашему состоянию цели, а затем проверить их на "достаточно близко". Эта метрика "достаточно близко" может отличаться от вашей метрики расстояния или нет. Если вы используете евклидово расстояние, но очень важно, чтобы вы выбрали конфигурацию цели также поворачивается правильно, тогда вы можете изменить метрику "достаточно близко", чтобы посмотреть на различия в углах.
то, что "достаточно близко", полностью зависит от вас. Кроме того, что-то для вас, чтобы настроить, и есть миллион документов, которые пытаются получить вас гораздо ближе в первую очередь.
вывод
эта случайная выборка может показаться смешной, но ваше дерево будет расти, чтобы исследовать ваше свободное пространство очень быстро. См. некоторые видео youtube на RRT для планирования пути. Мы не могу гарантировать то, что называется "вероятностной полнотой" с динамическими ограничениями, но обычно это "достаточно хорошо". Иногда возможно, что решение не существует, поэтому вам нужно будет поместить туда некоторую логику, чтобы остановить рост дерева через некоторое время (например, 20 000 образцов)
Больше Ресурсов:
начните с них, а затем начните изучать их цитаты, а затем начните изучать, кто цитирует их.
Это не ответ, но это слишком долго, чтобы поместить в качестве комментария.
прежде всего, реальное решение будет включать в себя оба линейное программирование (для многомерной оптимизации с ограничениями, которые будут использоваться во многих подстанциях), а также методы, используемые в траектория оптимизации и/или теории управления. Это очень сложная проблема, и если вы можете ее решить, вы можете получить работу в любой компании по вашему выбору. Единственное, что могло сделать эту проблему хуже будет трение (перетащить) эффекты или внешние эффекты гравитации тела. Реальное решение также идеально использовать интеграцию Верле или 4-го порядка Рунге Кутта, которые предлагают улучшения по сравнению с интеграцией Эйлера, которую вы реализовали здесь.
во-вторых, я верю вашим "2-я альтернативная версия" вашего вопроса выше опущено вращательное влияние на вектор позиционного смещения, который вы добавляете в позицию при каждом шаге. В то время как реактивные оси все остаются неподвижными относительно системы отсчета корабля, они делают не остаются неподвижными относительно глобальной системы координат, которую вы используете для посадки корабля (в глобальных координат [0, 0, 0]). Таким образом,[Px', Py', Pz'] вектор (рассчитанный по системе координат судна) должен пройти соответствующее вращение во всех 3 измерениях до применения к глобальным координатам положения.
в-третьих, есть некоторые неявные предположения, которые вы не смогли указать. Для например, одно измерение должно быть определено как измерение "глубина посадки", а отрицательные значения координат должны быть запрещены (если вы не принимаете Fiery crash). Я разработал макет модели для этого, в котором я предположил z размер, который будет размером посадки. Эта проблема очень чувствительна к исходному состоянию и ограничениям, наложенным на струи. Все мои попытки, используя Ваш пример начальных условий выше не удалось приземлиться. Например, в моем макете (без 3D-вектора смещения вращение, отмеченное выше), ограничения струи позволяют вращаться только в одном направлении по оси Z. Так что если aZ становится отрицательным в любое время (что часто бывает) корабль фактически вынужден завершить еще один полный оборот на этой оси, прежде чем он сможет даже попытаться снова приблизиться к нулю градусов. Кроме того, без вращения вектора 3D-смещения вы найдете, что Px будет только отрицательным, используя Ваш пример начальных условий и ограничений, и корабль вынужден либо разбиться, либо отклоняйтесь все дальше и дальше на отрицательную ось x, когда она пытается маневрировать. Единственный способ решить эту проблему-действительно включить вращение или обеспечить достаточные положительные и отрицательные реактивные силы.
однако, даже когда я ослабил ваши минимальные / максимальные ограничения силы, я не смог заставить мой макет успешно приземлиться, демонстрируя, насколько сложное планирование, вероятно, потребуется здесь. Если невозможно полностью сформулировать эту проблему в пространстве линейного программирования, я верю вам необходимо будет включить расширенное планирование или стохастические деревья решений, которые достаточно "умны", чтобы постоянно использовать вращательные методы для переориентации наиболее гибких струй на наиболее необходимые в настоящее время оси.
наконец, как я отметил в разделе комментариев, "14 мая 2015 года исходный код космических инженеров был предоставлен общественности на GitHub."Если вы считаете, что игра уже содержит эту логику, это должно быть вашим отправным пунктом. Однако, я подозреваю, что вы связаны разочароваться. Большинство последовательностей посадки космической игры просто берут под контроль корабль и не имитируют "реальные" векторы силы. После того, как вы возьмете под контроль трехмерную модель, очень легко предопределить 3d-сплайн с вращением, которое позволит кораблю мягко приземлиться и с идеальным подшипником в заданное время. Зачем любому программисту проходить через такой уровень работы для последовательности посадки? Такая логика может управлять ракетами МБР или планетарными вездеходами, и это просто перебор имхо для игры (если сама цель игры не состоит в том, чтобы увидеть, если вы можете посадить поврежденный космический корабль с произвольными струями и ограничениями без сбоев).
для такого рода проблем доступны два метода: поиск bruteforce и эвристика. Bruteforce означает распознавать проблему как черный ящик с входными и выходными параметрами, и цель состоит в том, чтобы получить правильные входные параметры для победы в игре. Чтобы запрограммировать такой поиск bruteforce, gamephysics работает в цикле моделирования (физическое моделирование) и через стохастический поиск (Минимакс, альфа-бета-обрезка) все возможности опробованы. Недостатком поиска bruteforce является высокое потребление процессора.
другие методы используют знания об игре. Знание о примитивах движения и об оценке. Эти знания запрограммирован с нормальным computerlanguages, как C++ или Java. Недостатком этой идеи является то, что часто бывает трудно понять знание.
лучшая практика для решения навигации космического корабля-объединить обе идеи в гибридную систему. Для программирования исходного кода для этой конкретной задачи я оцениваю почти 2000 строк кода не требуется. Такие проблемы обычно выполняются в рамках огромных проектов со многими программистами и занимают около 6 месяцев.
Я могу ввести другую технику в смесь (удивительных) предложенных ответов.
Он больше лежит в AI и обеспечивает близкие к оптимальным решения. Это называется Машинное Обучение, точнее Q-Learning. Это удивительно легко реализовать, но трудно получить право.
преимущество в том, что обучение может быть сделано offline, поэтому алгоритм может быть супер быстро при использовании.
вы может делать обучение, когда корабль построен или когда с ним что-то происходит (разрушение двигателя, большие куски оторваны...).
оптимальности
Я заметил, что вы ищете почти оптимальные решения. Ваш метод с параболами хорош для оптимального управления. Вот что ты сделал:--1-->
- наблюдать за состоянием системы.
- для каждого состояния (входит слишком быстро,слишком медленно, уходит, закрывается и т. д.) вы придумал действие (применить стратегию), что приведет систему в состояние ближе к цели.
- повторить
Это довольно трудно для человека в 3D (слишком много случаев, будет сводить вас с ума) машина может выучить где разделить параболы в каждом измерении, и разработать оптимальную стратегию собой.
Q-learning работает очень похоже на нас:
- соблюдать в (secretized) состоянии системы
- выберите действие на основе стратегия
- если это действие привело систему в желаемое состояние (ближе к цели), отметьте действие/начальное состояние как более желательное
- повторить
Дискретизация состояния вашей системы.
для каждого состояния есть карта intialized quasi-randomly, которая сопоставляет каждое состояние с действием (это the стратегия). Также назначьте желательность каждому состоянию (изначально ноль везде и 1000000 целевому состоянию (X=0, V=0).
- ваше государство было бы вашими 3 положениями, 3 углами, скоростью 3транслатион, и 3 скоростями вращения.
- ваши действия могут быть любой комбинацией двигателей
обучение
Тренируйте AI (автономная фаза):
- создать множество разнообразных ситуации
- применить стратегию
- оценить новое состояние
- пусть algo (см. ссылки выше) усиливает значение желательности выбранных стратегий.
живое использование в игре
через некоторое время появляется глобальная стратегия навигации. Затем вы храните его, и во время игрового цикла вы просто пробуете свою стратегию и применяете ее к каждой ситуации, когда они возникают.
стратегия все еще может учитесь на этом этапе, но, вероятно, медленнее (потому что это происходит в режиме реального времени). (Кстати, я мечтаю об игре, где ИИ будет учиться на обратной связи каждого пользователя, чтобы мы могли коллективно тренировать его^^)
попробуйте это в простой задаче 1D, он разрабатывает стратегию удивительно быстро (несколько секунд).
в 2D я считаю, что отличные результаты могут быть получены в течение часа.
для 3D... Вы смотрите на ночные вычисления. Есть несколько вещей, чтобы попробовать и ускорить процесс:
попытаться никогда 'забыть' предыдущие вычисления, и кормить их в качестве начальной стратегии "лучшее предположение". Сохраните его в файл!
вы можете сбросить некоторые состояния (например, крен корабля, может быть?) не теряя много оптимальности навигации, но значительно увеличивая скорость вычислений. Возможно, измените референтные значения, чтобы корабль всегда был на оси X, таким образом, вы упадете x&y размеры!
государства, более часто встречающиеся, будут иметь надежную и очень оптимальную стратегию. Может быть, нормализовать состояние, чтобы ваше состояние корабля всегда было близко к "стандартному" состоянию?
обычно интервалы скоростей вращения могут быть ограничены безопасно (вы не хотите, чтобы корабль кувыркался дико, поэтому стратегия всегда будет "un-wind" эта скорость). Конечно, углы поворота дополнительно ограничены.
вы можете также возможно дискретизировать нелинейно позиции, потому что дальше от цели, точность не сильно влияет на стратегию.