Алгоритм backpropagation нейронной сети не работает в Python
Я пишу нейронную сеть на Python, следуя примеру здесь. Кажется, что алгоритм обратного захвата не работает, учитывая, что нейронная сеть не может произвести правильное значение (в пределах погрешности) после обучения 10 тысяч раз. В частности, я тренирую его для вычисления функции синуса в следующем примере:
import numpy as np
class Neuralnet:
def __init__(self, neurons):
self.weights = []
self.inputs = []
self.outputs = []
self.errors = []
self.rate = .1
for layer in range(len(neurons)):
self.inputs.append(np.empty(neurons[layer]))
self.outputs.append(np.empty(neurons[layer]))
self.errors.append(np.empty(neurons[layer]))
for layer in range(len(neurons)-1):
self.weights.append(
np.random.normal(
scale=1/np.sqrt(neurons[layer]),
size=[neurons[layer], neurons[layer + 1]]
)
)
def feedforward(self, inputs):
self.inputs[0] = inputs
for layer in range(len(self.weights)):
self.outputs[layer] = np.tanh(self.inputs[layer])
self.inputs[layer + 1] = np.dot(self.weights[layer].T, self.outputs[layer])
self.outputs[-1] = np.tanh(self.inputs[-1])
def backpropagate(self, targets):
gradient = 1 - self.outputs[-1] * self.outputs[-1]
self.errors[-1] = gradient * (self.outputs[-1] - targets)
for layer in reversed(range(len(self.errors) - 1)):
gradient = 1 - self.outputs[layer] * self.outputs[layer]
self.errors[layer] = gradient * np.dot(self.weights[layer], self.errors[layer + 1])
for layer in range(len(self.weights)):
self.weights[layer] -= self.rate * np.outer(self.outputs[layer], self.errors[layer + 1])
def xor_example():
net = Neuralnet([2, 2, 1])
for step in range(100000):
net.feedforward([0, 0])
net.backpropagate([-1])
net.feedforward([0, 1])
net.backpropagate([1])
net.feedforward([1, 0])
net.backpropagate([1])
net.feedforward([1, 1])
net.backpropagate([-1])
net.feedforward([1, 1])
print(net.outputs[-1])
def identity_example():
net = Neuralnet([1, 3, 1])
for step in range(100000):
x = np.random.normal()
net.feedforward([x])
net.backpropagate([np.tanh(x)])
net.feedforward([-2])
print(net.outputs[-1])
def sine_example():
net = Neuralnet([1, 6, 1])
for step in range(100000):
x = np.random.normal()
net.feedforward([x])
net.backpropagate([np.tanh(np.sin(x))])
net.feedforward([3])
print(net.outputs[-1])
sine_example()
выход не может быть близок к tanh(sin(3)) = 0.140190616. Я подозревал ошибку, связанную с неправильными индексами или выравнивание, но Numpy не вызывает никаких ошибок, подобных этим. Есть советы, где я ошибся?
EDIT: Я забыл добавить нейроны смещения. Вот обновленный код:
import numpy as np
class Neuralnet:
def __init__(self, neurons):
self.weights = []
self.outputs = []
self.inputs = []
self.errors = []
self.offsets = []
self.rate = .01
for layer in range(len(neurons)-1):
self.weights.append(
np.random.normal(
scale=1/np.sqrt(neurons[layer]),
size=[neurons[layer], neurons[layer + 1]]
)
)
self.outputs.append(np.empty(neurons[layer]))
self.inputs.append(np.empty(neurons[layer]))
self.errors.append(np.empty(neurons[layer]))
self.offsets.append(np.random.normal(scale=1/np.sqrt(neurons[layer]), size=neurons[layer + 1]))
self.inputs.append(np.empty(neurons[-1]))
self.errors.append(np.empty(neurons[-1]))
def feedforward(self, inputs):
self.inputs[0] = inputs
for layer in range(len(self.weights)):
self.outputs[layer] = np.tanh(self.inputs[layer])
self.inputs[layer + 1] = self.offsets[layer] + np.dot(self.weights[layer].T, self.outputs[layer])
def backpropagate(self, targets):
self.errors[-1] = self.inputs[-1] - targets
for layer in reversed(range(len(self.errors) - 1)):
gradient = 1 - self.outputs[layer] * self.outputs[layer]
self.errors[layer] = gradient * np.dot(self.weights[layer], self.errors[layer + 1])
for layer in range(len(self.weights)):
self.weights[layer] -= self.rate * np.outer(self.outputs[layer], self.errors[layer + 1])
self.offsets[layer] -= self.rate * self.errors[layer + 1]
def sine_example():
net = Neuralnet([1, 5, 1])
for step in range(10000):
x = np.random.uniform(-5, 5)
net.feedforward([x])
net.backpropagate([np.sin(x)])
net.feedforward([np.pi])
print(net.inputs[-1])
def xor_example():
net = Neuralnet([2, 2, 1])
for step in range(10000):
net.feedforward([0, 0])
net.backpropagate([-1])
net.feedforward([0, 1])
net.backpropagate([1])
net.feedforward([1, 0])
net.backpropagate([1])
net.feedforward([1, 1])
net.backpropagate([-1])
net.feedforward([1, 1])
print(net.outputs[-1])
def identity_example():
net = Neuralnet([1, 3, 1])
for step in range(10000):
x = np.random.normal()
net.feedforward([x])
net.backpropagate([x])
net.feedforward([-2])
print(net.outputs[-1])
identity_example()
1 ответов
я думаю, что вы тренируете NN в неправильном направлении. У вас есть цикл более 10000 итераций и подача нового образца в каждом цикле. В этом случае NN никогда не будет обучаться.
(утверждение неверно! Смотрите обновление! )
что нужно сделать, это создать большой массив истинных образцов Y = sin(X), дайте его вашей сети один раз и повторите над набором тренировки вперед и назад, для того чтобы уменьшить функция стоимости. Чтобы проверить алгоритм, вам может потребоваться построить функцию затрат в зависимости от номера итерации и убедиться, что стоимость снижается.
другим важным моментом является инициализация Весов. Ваши номера довольно большие, и сеть займет много времени, чтобы сойтись, особенно при использовании низких ставок. Это хорошая практика для генерации начальных весов в некотором небольшом диапазоне [-eps .. eps] единообразно.
в моем коде я реализовал две различные функции активации: sigmoid() и tanh(). Вам нужно масштабировать входные данные в зависимости от выбранной функции:[0 .. 1] и [-1 .. 1] соответственно.
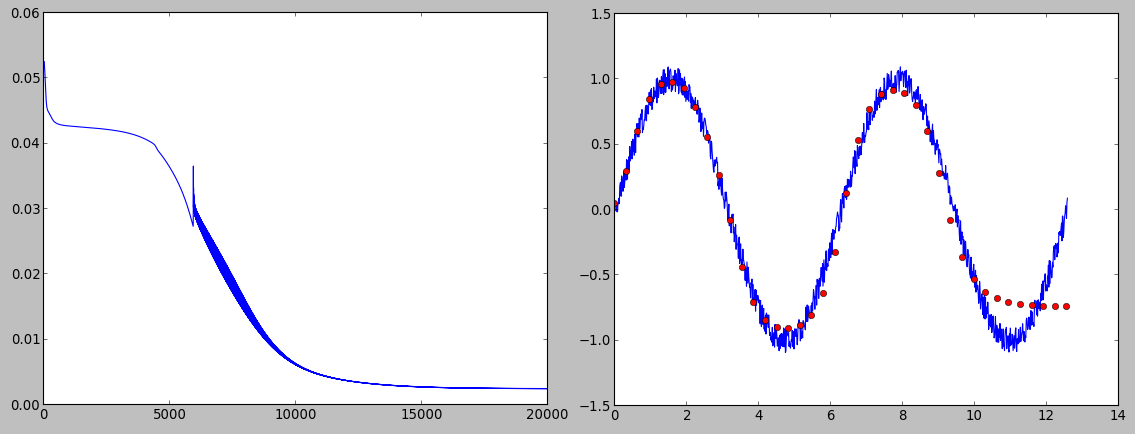
вот некоторые изображения, которые показывают функцию стоимости и результирующие прогнозы для sigmoid() и tanh() активация функции:
как вы можете видеть sigmoid() активация дает немного лучшие результаты, чем tanh().
также я получил гораздо лучшие прогнозы при использовании сети [1, 6, 1], по сравнению с более крупной сетью с 4 слоями [1, 6, 4, 1]. Таким образом, размер NN не всегда является решающим фактором. Вот прогноз для упомянутой сети с 4 слоями:
вот мой код с комментариями. Я пытался использовать твой ... обозначения там, где это было возможно.
import numpy as np
import math
import matplotlib.pyplot as plt
class Neuralnet:
def __init__(self, neurons, activation):
self.weights = []
self.inputs = []
self.outputs = []
self.errors = []
self.rate = 0.5
self.activation = activation #sigmoid or tanh
self.neurons = neurons
self.L = len(self.neurons) #number of layers
eps = 0.12; # range for uniform distribution -eps..+eps
for layer in range(len(neurons)-1):
self.weights.append(np.random.uniform(-eps,eps,size=(neurons[layer+1], neurons[layer]+1)))
###################################################################################################
def train(self, X, Y, iter_count):
m = X.shape[0];
for layer in range(self.L):
self.inputs.append(np.empty([m, self.neurons[layer]]))
self.errors.append(np.empty([m, self.neurons[layer]]))
if (layer < self.L -1):
self.outputs.append(np.empty([m, self.neurons[layer]+1]))
else:
self.outputs.append(np.empty([m, self.neurons[layer]]))
#accumulate the cost function
J_history = np.zeros([iter_count, 1])
for i in range(iter_count):
self.feedforward(X)
J = self.cost(Y, self.outputs[self.L-1])
J_history[i, 0] = J
self.backpropagate(Y)
#plot the cost function to check the descent
plt.plot(J_history)
plt.show()
###################################################################################################
def cost(self, Y, H):
J = np.sum(np.sum(np.power((Y - H), 2), axis=0))/(2*m)
return J
###################################################################################################
def feedforward(self, X):
m = X.shape[0];
self.outputs[0] = np.concatenate( (np.ones([m, 1]), X), axis=1)
for i in range(1, self.L):
self.inputs[i] = np.dot( self.outputs[i-1], self.weights[i-1].T )
if (self.activation == 'sigmoid'):
output_temp = self.sigmoid(self.inputs[i])
elif (self.activation == 'tanh'):
output_temp = np.tanh(self.inputs[i])
if (i < self.L - 1):
self.outputs[i] = np.concatenate( (np.ones([m, 1]), output_temp), axis=1)
else:
self.outputs[i] = output_temp
###################################################################################################
def backpropagate(self, Y):
self.errors[self.L-1] = self.outputs[self.L-1] - Y
for i in range(self.L - 2, 0, -1):
if (self.activation == 'sigmoid'):
self.errors[i] = np.dot( self.errors[i+1], self.weights[i][:, 1:] ) * self.sigmoid_prime(self.inputs[i])
elif (self.activation == 'tanh'):
self.errors[i] = np.dot( self.errors[i+1], self.weights[i][:, 1:] ) * (1 - self.outputs[i][:, 1:]*self.outputs[i][:, 1:])
for i in range(0, self.L-1):
grad = np.dot(self.errors[i+1].T, self.outputs[i]) / m
self.weights[i] = self.weights[i] - self.rate*grad
###################################################################################################
def sigmoid(self, z):
s = 1.0/(1.0 + np.exp(-z))
return s
###################################################################################################
def sigmoid_prime(self, z):
s = self.sigmoid(z)*(1 - self.sigmoid(z))
return s
###################################################################################################
def predict(self, X, weights):
m = X.shape[0];
self.inputs = []
self.outputs = []
self.weights = weights
for layer in range(self.L):
self.inputs.append(np.empty([m, self.neurons[layer]]))
if (layer < self.L -1):
self.outputs.append(np.empty([m, self.neurons[layer]+1]))
else:
self.outputs.append(np.empty([m, self.neurons[layer]]))
self.feedforward(X)
return self.outputs[self.L-1]
###################################################################################################
# MAIN PART
activation1 = 'sigmoid' # the input should be scaled into [ 0..1]
activation2 = 'tanh' # the input should be scaled into [-1..1]
activation = activation1
net = Neuralnet([1, 6, 1], activation) # structure of the NN and its activation function
##########################################################################################
# TRAINING
m = 1000 #size of the training set
X = np.linspace(0, 4*math.pi, num = m).reshape(m, 1); # input training set
Y = np.sin(X) # target
kx = 0.1 # noise parameter
noise = (2.0*np.random.uniform(0, kx, m) - kx).reshape(m, 1)
Y = Y + noise # noisy target
# scaling of the target depending on the activation function
if (activation == 'sigmoid'):
Y_scaled = (Y/(1+kx) + 1)/2.0
elif (activation == 'tanh'):
Y_scaled = Y/(1+kx)
# number of the iteration for the training stage
iter_count = 20000
net.train(X, Y_scaled, iter_count) #training
# gained weights
trained_weights = net.weights
##########################################################################################
# PREDICTION
m_new = 40 #size of the prediction set
X_new = np.linspace(0, 4*math.pi, num = m_new).reshape(m_new, 1);
Y_new = net.predict(X_new, trained_weights) # prediction
#rescaling of the result
if (activation == 'sigmoid'):
Y_new = (2.0*Y_new - 1.0) * (1+kx)
elif (activation == 'tanh'):
Y_new = Y_new * (1+kx)
# visualization
plt.plot(X, Y)
plt.plot(X_new, Y_new, 'ro')
plt.show()
raw_input('press any key to exit')
обновление
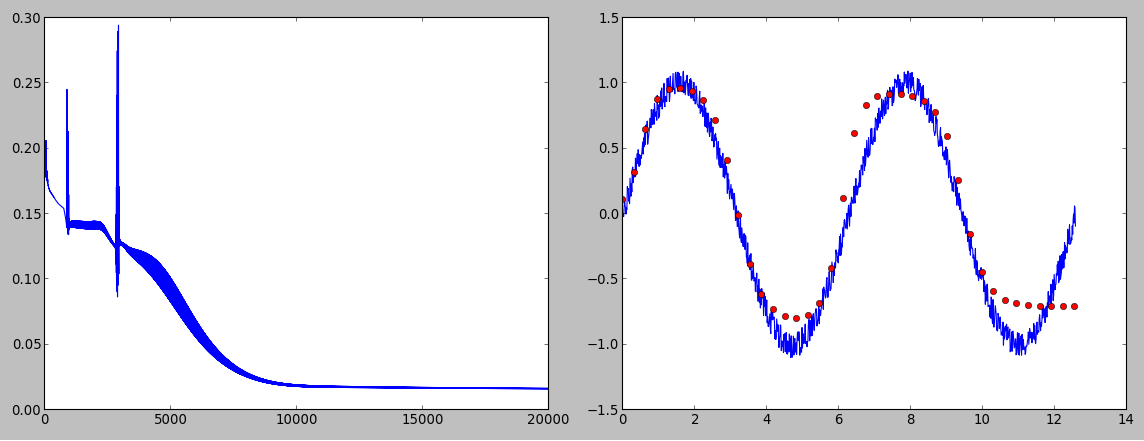
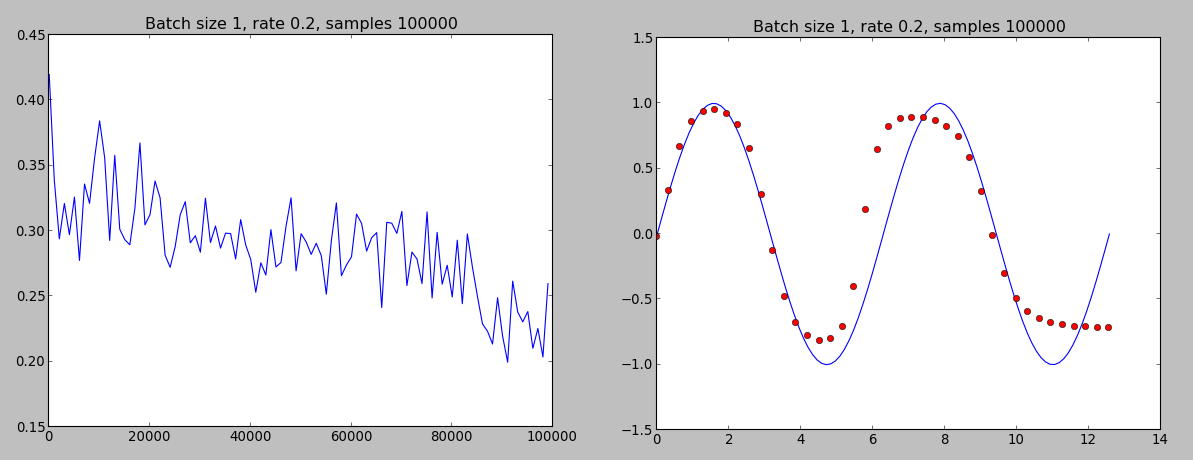
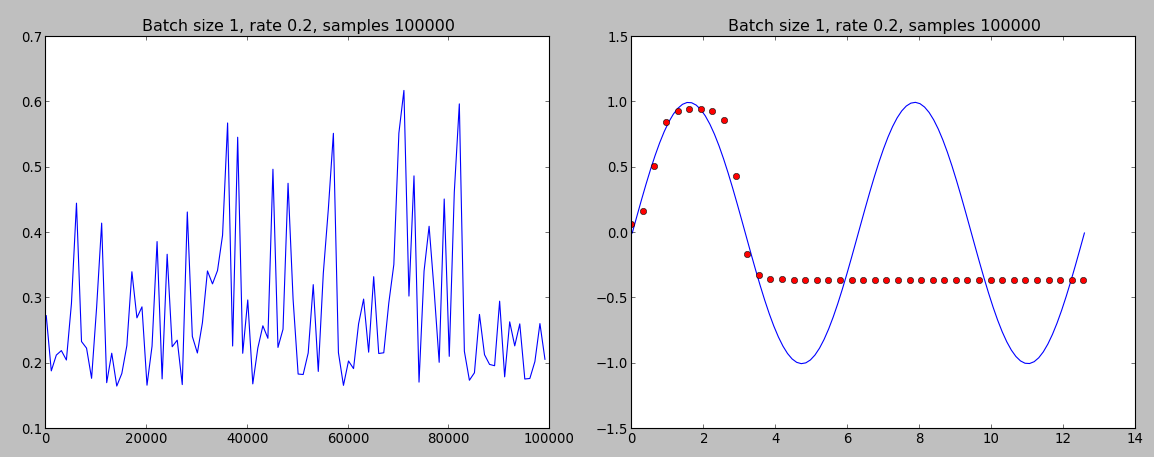
я хотел бы взять назад заявление относительно метода обучения, используемого в вашем коде. Сеть действительно можно обучить, используя только один образец на итерацию. Я получил интересные результаты в онлайн-обучении, используя как сигмовидные, так и танх-функции активации:
онлайн-тренировка с использованием сигмоида (функция затрат и предсказание)
онлайн-обучение с использованием Tanh (функция затрат и прогнозирование)
как можно видеть выбор сигмовидной как функция активации дает лучшую производительность. Функция стоимости выглядит не так хорошо, как во время автономного обучения, но, по крайней мере, она имеет тенденцию снижаться.
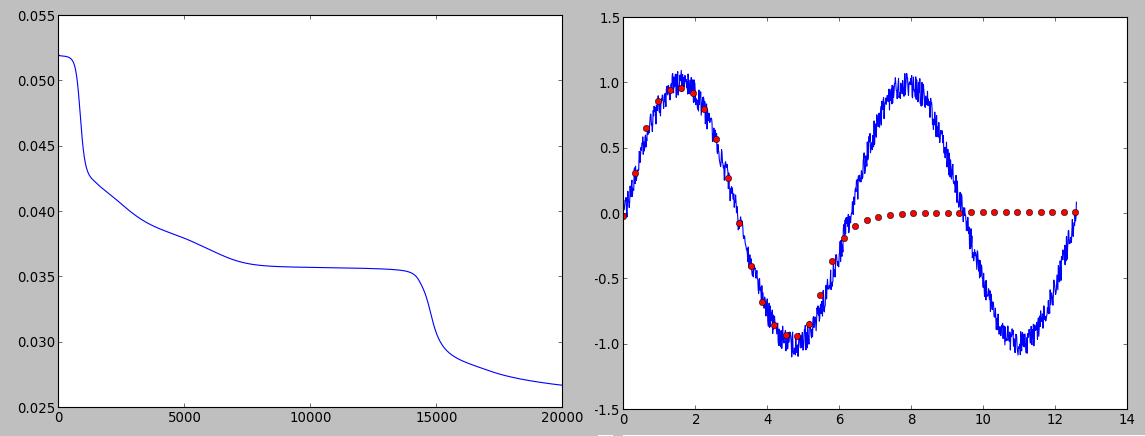
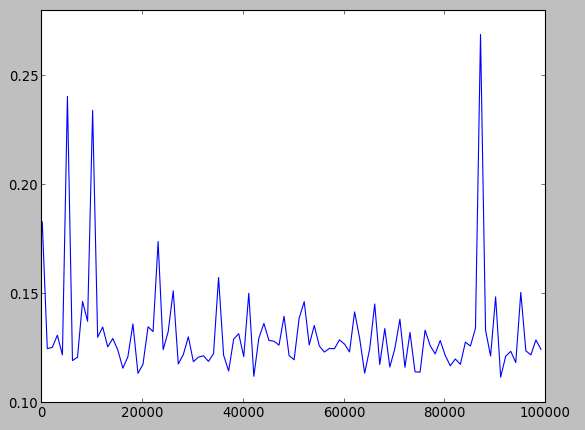
я построил функцию стоимости в вашей реализации, она выглядит довольно вяленое также:
может быть, это хорошая идея, чтобы попробовать свой код с сигмовидной или даже функции ReLU.
вот обновленный исходный код. Переключение между online и offline режимы обучения просто изменить method переменной.
import numpy as np
import math
import matplotlib.pyplot as plt
class Neuralnet:
def __init__(self, neurons, activation):
self.weights = []
self.inputs = []
self.outputs = []
self.errors = []
self.rate = 0.2
self.activation = activation #sigmoid or tanh
self.neurons = neurons
self.L = len(self.neurons) #number of layers
eps = 0.12; #range for uniform distribution -eps..+eps
for layer in range(len(neurons)-1):
self.weights.append(np.random.uniform(-eps,eps,size=(neurons[layer+1], neurons[layer]+1)))
###################################################################################################
def train(self, X, Y, iter_count):
m = X.shape[0];
for layer in range(self.L):
self.inputs.append(np.empty([m, self.neurons[layer]]))
self.errors.append(np.empty([m, self.neurons[layer]]))
if (layer < self.L -1):
self.outputs.append(np.empty([m, self.neurons[layer]+1]))
else:
self.outputs.append(np.empty([m, self.neurons[layer]]))
#accumulate the cost function
J_history = np.zeros([iter_count, 1])
for i in range(iter_count):
self.feedforward(X)
J = self.cost(Y, self.outputs[self.L-1])
J_history[i, 0] = J
self.backpropagate(Y)
#plot the cost function to check the descent
#plt.plot(J_history)
#plt.show()
###################################################################################################
def cost(self, Y, H):
J = np.sum(np.sum(np.power((Y - H), 2), axis=0))/(2*m)
return J
###################################################################################################
def cost_online(self, min_x, max_x, iter_number):
h_arr = np.zeros([iter_number, 1])
y_arr = np.zeros([iter_number, 1])
for step in range(iter_number):
x = np.random.uniform(min_x, max_x, 1).reshape(1, 1)
self.feedforward(x)
h_arr[step, 0] = self.outputs[-1]
y_arr[step, 0] = np.sin(x)
J = np.sum(np.sum(np.power((y_arr - h_arr), 2), axis=0))/(2*iter_number)
return J
###################################################################################################
def feedforward(self, X):
m = X.shape[0];
self.outputs[0] = np.concatenate( (np.ones([m, 1]), X), axis=1)
for i in range(1, self.L):
self.inputs[i] = np.dot( self.outputs[i-1], self.weights[i-1].T )
if (self.activation == 'sigmoid'):
output_temp = self.sigmoid(self.inputs[i])
elif (self.activation == 'tanh'):
output_temp = np.tanh(self.inputs[i])
if (i < self.L - 1):
self.outputs[i] = np.concatenate( (np.ones([m, 1]), output_temp), axis=1)
else:
self.outputs[i] = output_temp
###################################################################################################
def backpropagate(self, Y):
self.errors[self.L-1] = self.outputs[self.L-1] - Y
for i in range(self.L - 2, 0, -1):
if (self.activation == 'sigmoid'):
self.errors[i] = np.dot( self.errors[i+1], self.weights[i][:, 1:] ) * self.sigmoid_prime(self.inputs[i])
elif (self.activation == 'tanh'):
self.errors[i] = np.dot( self.errors[i+1], self.weights[i][:, 1:] ) * (1 - self.outputs[i][:, 1:]*self.outputs[i][:, 1:])
for i in range(0, self.L-1):
grad = np.dot(self.errors[i+1].T, self.outputs[i]) / m
self.weights[i] = self.weights[i] - self.rate*grad
###################################################################################################
def sigmoid(self, z):
s = 1.0/(1.0 + np.exp(-z))
return s
###################################################################################################
def sigmoid_prime(self, z):
s = self.sigmoid(z)*(1 - self.sigmoid(z))
return s
###################################################################################################
def predict(self, X, weights):
m = X.shape[0];
self.inputs = []
self.outputs = []
self.weights = weights
for layer in range(self.L):
self.inputs.append(np.empty([m, self.neurons[layer]]))
if (layer < self.L -1):
self.outputs.append(np.empty([m, self.neurons[layer]+1]))
else:
self.outputs.append(np.empty([m, self.neurons[layer]]))
self.feedforward(X)
return self.outputs[self.L-1]
###################################################################################################
# MAIN PART
activation1 = 'sigmoid' #the input should be scaled into [0..1]
activation2 = 'tanh' #the input should be scaled into [-1..1]
activation = activation1
net = Neuralnet([1, 6, 1], activation) # structure of the NN and its activation function
method1 = 'online'
method2 = 'offline'
method = method1
kx = 0.1 #noise parameter
###################################################################################################
# TRAINING
if (method == 'offline'):
m = 1000 #size of the training set
X = np.linspace(0, 4*math.pi, num = m).reshape(m, 1); #input training set
Y = np.sin(X) #target
noise = (2.0*np.random.uniform(0, kx, m) - kx).reshape(m, 1)
Y = Y + noise #noisy target
#scaling of the target depending on the activation function
if (activation == 'sigmoid'):
Y_scaled = (Y/(1+kx) + 1)/2.0
elif (activation == 'tanh'):
Y_scaled = Y/(1+kx)
#number of the iteration for the training stage
iter_count = 20000
net.train(X, Y_scaled, iter_count) #training
elif (method == 'online'):
sampling_count = 100000 # number of samplings during the training stage
m = 1 #batch size
iter_count = sampling_count/m
for layer in range(net.L):
net.inputs.append(np.empty([m, net.neurons[layer]]))
net.errors.append(np.empty([m, net.neurons[layer]]))
if (layer < net.L -1):
net.outputs.append(np.empty([m, net.neurons[layer]+1]))
else:
net.outputs.append(np.empty([m, net.neurons[layer]]))
J_history = []
step_history = []
for i in range(iter_count):
X = np.random.uniform(0, 4*math.pi, m).reshape(m, 1)
Y = np.sin(X) #target
noise = (2.0*np.random.uniform(0, kx, m) - kx).reshape(m, 1)
Y = Y + noise #noisy target
#scaling of the target depending on the activation function
if (activation == 'sigmoid'):
Y_scaled = (Y/(1+kx) + 1)/2.0
elif (activation == 'tanh'):
Y_scaled = Y/(1+kx)
net.feedforward(X)
net.backpropagate(Y_scaled)
if (np.remainder(i, 1000) == 0):
J = net.cost_online(0, 4*math.pi, 1000)
J_history.append(J)
step_history.append(i)
plt.plot(step_history, J_history)
plt.title('Batch size ' + str(m) + ', rate ' + str(net.rate) + ', samples ' + str(sampling_count))
#plt.ylim([0, 0.1])
plt.show()
#gained weights
trained_weights = net.weights
##########################################################################################
# PREDICTION
m_new = 40 #size of the prediction set
X_new = np.linspace(0, 4*math.pi, num = m_new).reshape(m_new, 1);
Y_new = net.predict(X_new, trained_weights) #prediction
#rescaling of the result
if (activation == 'sigmoid'):
Y_new = (2.0*Y_new - 1.0) * (1+kx)
elif (activation == 'tanh'):
Y_new = Y_new * (1+kx)
#visualization
#fake sine curve to show the ideal signal
if (method == 'online'):
X = np.linspace(0, 4*math.pi, num = 100)
Y = np.sin(X)
plt.plot(X, Y)
plt.plot(X_new, Y_new, 'ro')
if (method == 'online'):
plt.title('Batch size ' + str(m) + ', rate ' + str(net.rate) + ', samples ' + str(sampling_count))
plt.ylim([-1.5, 1.5])
plt.show()
raw_input('press any key to exit')
теперь у меня есть некоторые замечания к вашему текущему коду:
ваша функция синуса выглядит следующим образом:
def sine_example():
net = Neuralnet([1, 6, 1])
for step in range(100000):
x = np.random.normal()
net.feedforward([x])
net.backpropagate([np.tanh(np.sin(x))])
net.feedforward([3])
print(net.outputs[-1])
I не знаю, почему вы используете tanh в своем целевом вводе. Если вы действительно хотите использовать tanh синуса в качестве цели, вам нужно масштабировать его до [-1..1], потому что tanh(sin (x)) возвращает значения в диапазоне [-0.76..0.76].
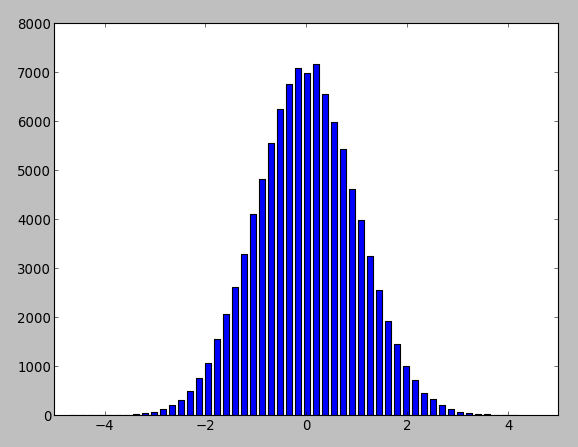
следующее-это диапазон вашего тренировочного набора. Вы используете x = np.random.normal() для создания образцов. Вот распределение такого ввода:
после этого вы хотите, чтобы ваша сеть предсказала синус 3, но в сети есть почти никогда не видел такого числа на тренировочном этапе. Вместо этого я бы использовал равномерное распределение в более широком диапазоне для генерации образцов.