Алгоритм дерева суффиксов Ukkonen на простом английском языке
Я чувствую себя немного Толстым в этот момент. Я потратил дни, пытаясь полностью обернуть голову вокруг конструкции суффиксного дерева, но поскольку у меня нет математического фона, многие объяснения ускользают от меня, поскольку они начинают чрезмерно использовать математическую символику. Самое близкое к хорошему объяснению, которое я нашел, это Быстрый Поиск Строки С Суффиксом Деревья, но он замазывает различные точки, и некоторые аспекты алгоритма остаются непонятный.
пошаговое объяснение этого алгоритма здесь, на переполнении стека, было бы неоценимым для многих других, кроме меня, я уверен.
для справки, вот статья Укконена об алгоритме:http://www.cs.helsinki.fi/u/ukkonen/SuffixT1withFigs.pdf
мое основное понимание, до сих пор:
- мне нужно перебрать каждый префикс P данной строки t
- мне нужно перебирать каждый суффикс S в префикс P и добавьте его в дерево
- чтобы добавить суффикс S к дереву, мне нужно перебрать каждый символ в S, причем итерации состоят из либо хождения по существующей ветви, которая начинается с того же набора символов C в S, и потенциально расщепления ребра на нисходящие узлы, когда я достигаю другого символа в суффиксе, либо если не было совпадающего ребра, чтобы идти вниз. Если для C не найдено совпадающего ребра, создается новое ребро листа для С.
основной алгоритм выглядит как O (n2), как указано в большинстве объяснений, так как нам нужно пройти через все префиксы, то нам нужно пройти через каждый из суффиксов для каждого префикса. Алгоритм укконена, по-видимому, уникален из-за метода указателя суффикса, который он использует, хотя я думаю это это то, что мне трудно понять.
У меня также возникли проблемы понимание:
- точно, когда и как "активная точка" назначается, используется и изменяется
- что происходит с аспектом канонизации алгоритма
- почему реализации, которые я видел, нужно "исправить" ограничивающие переменные, которые они используют
в результате C# исходный код. Он не только работает правильно, но поддерживает автоматическую канонизацию и отображает более красивый текстовый график выход. Исходный код и образец вывода:
обновление 2017-11-04
спустя много лет я нашел новое использование для деревьев суффиксов и реализовал алгоритм в JavaScript. Суть ниже. Он должен быть без ошибок. Сбросьте его в файл js,npm install chalk из того же места, а затем запустите с node.JS, чтобы увидеть некоторые красочный выход. Есть урезанная версия в той же самой сути, без какого-либо отладочного кода.
https://gist.github.com/axefrog/c347bf0f5e0723cbd09b1aaed6ec6fc6
6 ответов
ниже приводится попытка описать алгоритм Укконена, сначала показав, что он делает, когда строка проста (т. е. не содержит повторяющихся символов), а затем расширяя ее до полного алгоритма.
во-первых, несколько предварительных заявлений.
то, что мы строим, - это в принципе как поиск trie. Так есть является корневым узлом, ребра выходят из него, приводя к новым узлам, и дальше края выходят из них, и так далее
но: в отличие от поиска trie, метки края не являются одиночными письмена. Вместо этого, каждое ребро помечается с помощью пары чисел
[from,to]. Это указатели на текст. В этом смысле каждый edge несет строковую метку произвольной длины, но принимает только O (1) пробел (два указателя).
основной принцип
я хотел бы сначала показано, как создать дерево-суффикс особенно простая строка, строка без повторяющихся символов:
abc
алгоритм работает в шагах, слева направо. Есть один шаг для каждого символа строки. Каждый шаг может включать несколько отдельных операций, но мы увидим (см. заключительные наблюдения в конце), что общее количество операций равно O(n).
Итак, начнем с левый, и сначала вставьте только один символ
a путем создания ребра от корневого узла (слева) до листа,
и маркировка его как [0,#], что означает, что край представляет
подстрока, начинающаяся с позиции 0 и заканчивающаяся на текущего. Я
используйте символ # означает текущего, который находится в позиции 1
(сразу после a).
Итак, у нас есть начальное дерево, которое выглядит так это:
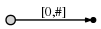
и это означает следующее:
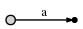
теперь мы переходим к позиции 2 (сразу после b). наша цель на каждом шагу
вставить все суффиксы до текущей позиции. Мы делаем это
by
- расширение существующей
a-edge toab - вставка одного нового края для
b
In наше представление это выглядит так:
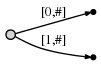
и это означает:
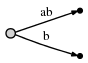
мы видим две вещи:
- представление ребра для
abis тот же как это было в начальном дереве:[0,#]. Его значение автоматически изменилось потому что мы обновили текущую позицию#от 1 до 2. - каждый край потребляет O(1) пространство, потому что оно состоит только из двух указатели на текст, независимо от количества символов представляет.
Далее мы снова увеличиваем позицию и обновляем дерево, добавляя
а c к каждому существующему краю и вводить один новый край для нового
суффикс c.
в нашем представлении это выглядит так:
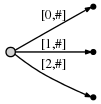
и что это значит есть:
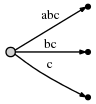
мы видим:
- дерево является правильным суффиксом tree до текущей позиции после каждого шага
- существует столько шагов, сколько символов в тексте
- объем работы на каждом шаге порядка O(1), поскольку все существующие края
обновляются автоматически путем увеличения
#, и вставив один новый край для финального персонажа может сделать в O (1) время. Следовательно, для строки длины n требуется только O(n) время.
первое расширение: простые повторения
конечно, это работает так хорошо только потому, что наша строка не содержат любые повторы. Теперь мы рассмотрим более реалистичную строку:
abcabxabcd
начинается с abc как и в предыдущем примере, то ab повторяется
а за ним -x, а потом abc повторяется с последующим d.
шаги с 1 по 3: после первых 3 шагов у нас есть дерево из предыдущего примера:
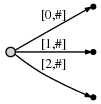
Шаг 4: мы движемся # на позицию 4. Это неявно обновляет все существующие
края этого:
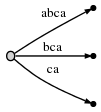
и нам нужно вставить последний суффикс текущего шага,a, at
корень.
прежде чем мы сделаем это, мы вводим еще две переменные (в дополнение к
#), которые, конечно, были там все время, но мы не использовали
им пока:
- на активные точки, который является тройной
(active_node,active_edge,active_length) - на
remainder, которое является целым числом, указывающим, сколько новых суффиксов нам нужно вставить
точное значение этих двух скоро станет ясно, но пока скажем так:
- In простой
abcнапример, активная точка всегда была(root,'x',0), то естьactive_nodeбыл корневого узлаactive_edgeбыл указан как нулевой символ'x'иactive_lengthбыл ноль. Результатом этого было то, что один новый край, который мы вставили в каждый шаг был вставлен в корневом узле как недавно созданный край. Скоро мы увидим, почему тройка необходима для представлять эту информацию. - на
remainderвсегда было установлено значение 1 в начале каждого шаг. Смысл этого было ли это количество суффиксов, которые мы должны были активно вставить в конце каждого шага было 1 (всегда только финальный персонаж).
теперь это изменится. Когда мы вставляем текущий финал
характер a в корне мы замечаем, что уже есть исходящий
край, начинающийся с a, а именно: abca. Вот что мы делаем в
такой случай:
- мы не вставить свежий краю
[4,#]в корневом узле. Вместо мы просто обратите внимание, что суффиксaуже в наши дерево. Он заканчивается в середине более длинного края, но мы не обеспокоенный этим. Мы просто оставим все как есть. - мы установить активную точку to
(root,'a',1). Это означает, что активный точка теперь находится где-то посередине исходящего края корневого узла, который начинается сa, в частности, после позиции 1 на этом краю. Мы обратите внимание, что edge задается просто его первым характерa. Этого достаточно, потому что может быть единственный края начиная с любого конкретного символа (подтвердите, что это верно после прочтения всего описания). - мы также прирастить
remainder, поэтому в начале следующего шага будет 2.
наблюдения: когда в финале суффикс нужно вставить найдены
существуют в дереве уже дерево не менял at все (мы обновляем только активную точку и remainder). Дерево
тогда не является точным представлением дерева суффиксов до
текущая позиция, но это содержит все суффиксы (потому что окончательный
суффикс a содержится имплицитно). Следовательно, помимо обновления
переменные (которые все фиксированной длины, так что это O (1)), там было
не работает сделать на этом шаге.
шаг 5: мы обновляем текущую позицию # в 5. Этот
автоматически обновляет дерево следующим образом:
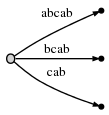
и , потому что remainder is 2 нам нужно вставить два последних
суффиксы текущей позиции:ab и b. Это в основном потому, что:
- на
aсуффикс с предыдущего шага никогда не был должным образом вставленный. Так оно и есть остались, и так как мы развивали один шаг, он теперь вырос изatoab. - и нам нужно вставить новый конечный край
b.
на практике это означает, что мы идем к активной точке (которая указывает на
за a на abcab edge) и вставьте
текущий финальный символ b. но: опять же, оказывается, что b is
также уже присутствует на том же краю.
Итак, опять же, мы не меняем дерево. Мы просто:
- обновить активную точку до
(root,'a',2)(тот же узел и край как и раньше, но теперь мы заb) - увеличить
remainderдо 3, потому что мы все еще не должным образом вставлено последнее ребро с предыдущего шага, и мы не вставляем текущий конечный край либо.
чтобы быть ясным: мы должны были вставить ab и b на текущем шаге, но
потому что ab был уже найден, мы обновили активный точки и сделал
даже не пытайтесь вставить b. Почему? Потому что если ab в дереве,
каждый суффикс (включая b) должно быть в дереве,
тоже. Может быть, только имплицитно, но он должен быть там, из-за
так мы построили дерево до сих пор.
переходим к Шаг 6 путем увеличения #. Дерево
автоматически обновляется до:
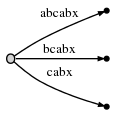
потому что remainder is 3, мы должны вставить abx, bx и
x. Активная точка сообщает нам, где ab заканчивается, поэтому нам нужно только
прыгайте туда и вставьте x. Действительно,x еще нет, поэтому мы
разделите abcabx edge и вставьте внутренний узел:
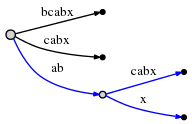
края представления еще указатели в тексте, так разделение и вставка внутреннего узла можно выполнить за O (1) Время.
так мы разобрались с abx и декремента remainder в 2. Теперь мы
нужно вставить следующий оставшийся суффикс,bx. Но прежде чем мы это сделаем
нам нужно обновить активную точку. Правило для этого, после разделения
и вставка ребра, будет называться Правило 1 ниже, и он применяется всякий раз, когда
active_node is root (далее мы узнаем Правило 3 для других случаев
ниже.) Здесь Правило 1:
после вставки из root,
active_nodeостается rootactive_edgeустанавливается на первый символ Нового суффикса we нужно вставить, то естьbactive_lengthуменьшается на 1
следовательно, новая тройка активной точки (root,'b',1) указывает, что
следующая вставка должна быть сделана в bcabx края, за 1 символ,
т. е. за b. Мы можем определить точку вставки за O(1) времени и
проверьте ли x is уже есть или нет. Если он присутствовал, то мы
закончит текущий шаг и оставит все как есть. Но!--19-->
нет, поэтому вставляем его путем расщепления ребра:
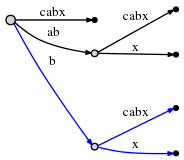
опять же, это заняло O (1) Время, и мы обновляем remainder 1, а
активная точка на (root,'x',0) как гласит Правило 1.
но есть еще одна вещь, которую нам нужно сделать. Мы назовем это Правило 2:
если мы разделим edge и вставьте новый узел, и если это не первый узел созданный во время текущего шага, мы соединяем ранее вставленный узел и новый узел через специальный указатель, a суффикс ссылка. Далее мы увидим, почему это полезно. Вот что мы получаем: суффикс ссылка представлена в виде пунктирного края:
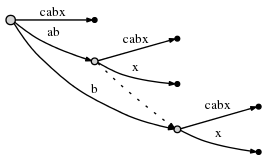
нам все еще нужно вставить окончательный суффикс текущего шага,
x. Поскольку active_length компонент активного узла упал
до 0 окончательная вставка производится непосредственно в корне. Так как нет
исходящий край в корневом узле, начиная с x, вставляем новый
edge:
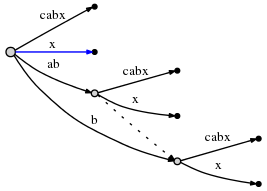
как видим, на текущем шаге были сделаны все остальные вставки.
переходим к Шаг 7 установка #=7, который автоматически добавляет следующий символ,
a, ко всем краям листа, как всегда. Затем мы пытаемся вставить новый финал
символ в активную точку (корень), и найти, что он там
уже. Таким образом, мы заканчиваем текущий шаг, не вставляя ничего и
обновите активную точку до (root,'a',1).
на Шаг 8, #=8, мы добавляем b, и как видно раньше, это только
означает, что мы обновляем активную точку до (root,'a',2) и надбавка remainder не делая
все остальное, потому что b уже присутствует. , мы замечаем (в O (1) время), что активная точка
теперь в конце края. Мы отражаем это, переназначая его на
(node1,'x',0). Здесь я использую node1 для обозначения
внутренний узел ab края заканчивается.
затем в шаг #=9, нам нужно вставить "c" , и это поможет нам
поймите последний трюк:
второе расширение: использование суффиксных ссылок
как всегда # обновление добавляет c автоматически к листу стыки
и мы идем к активной точке, чтобы посмотреть, можем ли мы вставить "c". Получается
out ' c ' уже существует на этом краю, поэтому мы устанавливаем активную точку
(node1,'c',1), increment remainder и ничего больше.
сейчас шаг #=10, remainder is 4, и поэтому нам сначала нужно вставить
abcd (который остается от 3 шагов назад), вставив d на активных
точка.
пытается вставить d в активной точке вызывает разделение ребра в
O (1) время:
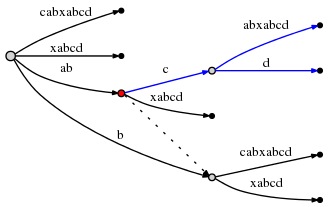
на active_node, из которого был инициирован раскол, отмечен в
красный вверху. Вот последнее правило:--174-->Правило 3:
после разделения ребра от
active_nodeэто не корень узел, мы следуем за суффиксной ссылкой, выходящей из этого узла, если есть любой, и сброситьactive_nodeк узлу, на который он указывает. Если есть нет суффиксной ссылки, мы устанавливаемactive_nodeв корень.active_edgeиactive_lengthостаются неизменными.
таким образом, активная точка теперь (node2,'c',1) и node2 отмечен в
красный внизу:
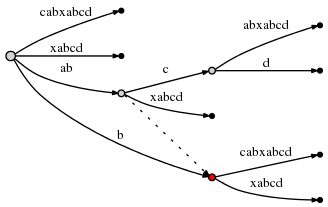
с момента вставки abcd завершено, мы декремента remainder в
3 и рассмотрим следующий оставшийся суффикс текущего шага,
bcd. Правило 3 установило активную точку только на правый узел и край
Итак, вставка bcd можно сделать, просто вставив его окончательный символ
d в активная точка.
это вызывает еще один раскол края, и из-за правила 2, мы необходимо создать суффикс-ссылку из ранее вставленного узла на новый один:
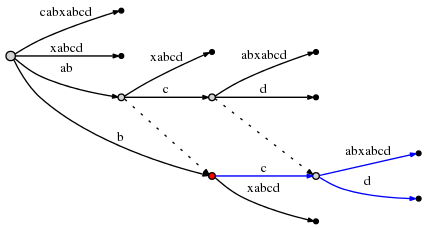
мы видим: связи суффикса позволяют мы переустановить активную точку поэтому мы
может сделать следующий осталось вставить при O (1) усилии. Посмотрите на
график выше, чтобы подтвердить, что действительно узел на метку ab это связано с
этот узел на b (его суффикс), а узел на abc это связано с
bc.
текущий шаг еще не закончен. remainder теперь 2, и мы
нужно следовать правилу 3 для сброса активной точки. Поскольку
ток active_node (красный выше) не имеет ссылки суффикса, мы сбрасываем на
корень. Активная точка теперь (root,'c',1).
следовательно, следующая вставка происходит на одном исходящем краю корневого узла
чей ярлык начинается с c: cabxabcd за первый характер,
т. е. за c. Это вызывает еще один раскол:
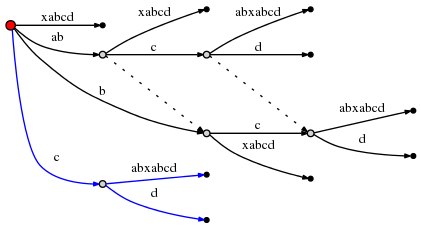
и поскольку это связано с созданием нового внутреннего узла, мы следуем Правило 2 и установить новый суффикс ссылки из ранее созданного внутреннего узел:
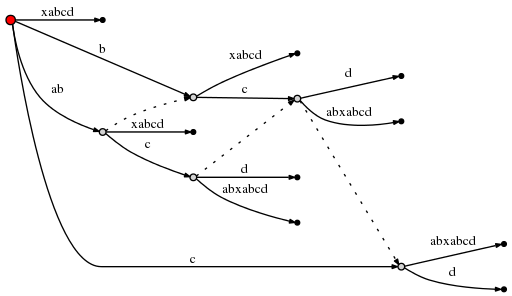
(я использую Graphviz Dot для таких маленьких диаграммы. Новая ссылка суффикса заставила dot перестроить существующую края, поэтому проверяйте тщательно, чтобы убедиться, что единственное это было вверху вставлена новая суффикс-ссылка.)
с этим remainder может быть установлено значение 1 и так как active_node это
root, мы используем правило 1 для обновления активной точки до (root,'d',0). Этот
означает, что последняя вставка текущего шага должна вставить одно d
в корне:
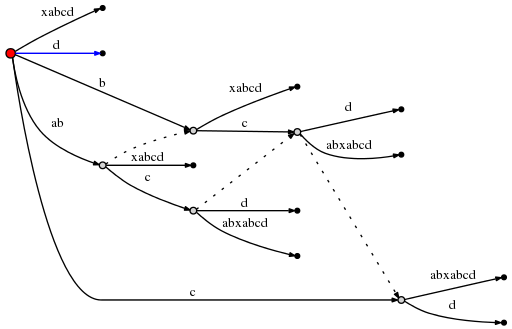
это был последний шаг, и мы сделали. Есть количество финал наблюдения, но:
в каждом шагом мы движемся
#вперед на 1 позицию. Это автоматически обновления всех вершин за O(1) времени.но он не имеет дело с a) любые суффиксы оставшиеся из предыдущих шаги, и б) с одним заключительным символом текущего шага.
remainderговорит нам, сколько дополнительных вставок нужно делать. Эти вставки соответствуют один-к-одному к окончательным суффиксам строка, которая заканчивается на текущей позиция#. Мы рассматриваем один после другого и сделайте вставку. важно: каждая вставка сделано в O (1) раз, так как активная точка говорит нам, где именно go, и нам нужно добавить только один символ в active точка. Почему? Потому что другие символы содержатся имплицитно (в противном случае активная точка не была бы там, где она есть).после каждой такой вставки мы уменьшаем
remainderи следовать суффикс ссылку, если есть. Если нет, переходим к root (Правило 3). Если мы в корне уже, мы модифицируем активную точку, используя правило 1. В любом случае, требуется только O(1) времени.если во время одной из этих вставок мы обнаружим, что символ, который мы хотим чтобы вставить уже есть, мы ничего не делаем и заканчиваем текущий шаг, даже если
remainder>0. Причина в том, что любой оставшиеся вставки будут суффиксами того, который мы только что пытались делать. Поэтому они все подразумевается в текущем дереве. Факт этоremainder> 0 гарантирует, что мы имеем дело с оставшимися суффиксами позже.что делать, если в конце алгоритма
remainder>0? Это будет case всякий раз, когда конец текста является подстрокой, которая произошла где-то раньше. В этом случае мы должны добавить один дополнительный символ в конце строки, которая не произошла раньше. В литература, обычно знак доллара$используется в качестве символа для что. почему это важно? --> если позже мы используем дерево завершенных суффиксов для поиска суффиксов, мы должны принимать совпадения только в том случае, если они конец на листе. В противном случае мы получили бы много ложных совпадений, потому что есть много строки имплицитно содержится в дереве, которое не является фактическими суффиксами основной строки. Принуждениеremainderбыть 0 в конце-это, по сути, способ гарантировать, что все суффиксы заканчиваются на листе узел. , если мы хотим использовать дерево для поиска общие подстроки не только суффиксы из основной строки Этот последний шаг действительно не требуется, как это предлагается в комментарии OP ниже.Итак, какова сложность всего алгоритма? Если текст равен n символов в длину, очевидно, n шагов (или N+1, если мы добавим знак доллара.) На каждом шагу мы либо ничего не делаем (другое чем обновление переменных), или мы делаем
remainderвставки, каждая из которых принимает O(1) время. Сremainderпоказывает, сколько раз мы ничего не сделали в предыдущих шагах, и уменьшается для каждой вставки, что мы делаем теперь общее количество раз, когда мы что-то делаем, равно N (или n+1). Следовательно, общая сложность равна O (n).однако есть одна маленькая вещь, которую я не объяснил должным образом: Может случиться так, что мы перейдем по суффиксной ссылке, обновим активный точка, а потом найти, что его
active_lengthкомпонент не хорошо работайте с новымactive_node. Например, рассмотрим ситуацию вот так:

(пунктирные линии указывают на остальную часть дерева. Пунктирная линия суффикс ссылка.)
теперь пусть активная точка будет (red,'d',3), поэтому он указывает на место
за f на defg edge. Теперь предположим, что мы сделали необходимое
обновления и теперь перейдите по ссылке суффикса обновить активную точку
согласно правилу 3. Новая активная точка (green,'d',3). Однако,
the d-край выходит из зеленого узла de, поэтому он имеет только 2
письмена. Чтобы найти правильную активную точку, мы, очевидно,
нужно следовать этому краю до синего узла и сбросить до (blue,'f',1).
в особенно плохом случае,active_length может быть как большой, как
remainder, который может быть размером с n. И это вполне может случиться.
чтобы найти правильную активную точку, мы нужно не только перепрыгнуть через одну
внутренний узел, но, возможно, много, до n в худшем случае. Сделать это
означает, что алгоритм имеет скрытый O (n2) сложность, потому что
в каждом шаге remainder, как правило, O (n) и коррективы по месту службы
к активному узлу после следования суффикса ссылка может быть O (n), тоже?
нет. Причина в том, что если мы действительно должны настроить активную точку
(например, от зеленого до синего, как указано выше), что приводит нас к новому узлу, который
имеет собственный суффикс link, и active_length будет сокращена. Как
следуем по цепочке суффиксных звеньев делаем оставшиеся вставки,active_length только
уменьшите, и число регулировок активн-пункта мы можем сделать дальше
путь не может быть больше active_length в любой момент времени. С
active_length не может превышать remainder и remainder
является O (n) не только на каждом шаге, но и общей суммой приращений
когда-либо сделал remainder в течение всего процесса
O (n) тоже число активных точек корректировки также ограничены
O (n).
я попытался реализовать дерево суффиксов с подходом, приведенным в ответе jogojapan, но это не сработало для некоторых случаев из-за формулировки, используемой для правил. Более того, я упомянул, что никому не удалось реализовать абсолютно правильное дерево суффиксов, используя этот подход. Ниже я напишу "обзор" ответа jogojapan с некоторыми изменениями в правилах. Я также опишу случай, когда мы забываем создать важно суффикс связи.
используются дополнительные переменные
- активные точки - тройка (active_node; active_edge; active_length), показывающая, откуда мы должны начать вставлять новый суффикс.
- остаток - показывает количество суффиксов, которые мы должны добавить явно. Например, если наше слово "abcaabca", а остаток = 3, это означает, что мы должны обработать 3 последних суффикса:bca, ca и a.
давайте использовать понятие внутренний узел - все узлы, кроме root и листья are внутренние узлы.
наблюдение 1
когда последний суффикс, который нам нужно вставить, уже существует в дереве, само дерево не изменяется вообще (мы только обновляем active point и remainder).
наблюдение 2
если в какой-то момент active_length больше или равно длине текущего ребра (edge_length), мы двигаем active point до edge_length строго больше active_length.
теперь, давайте определим правила:
Правило 1
если после вставки из активный узел = root, the активная длина is больше 0, то:
- активный узел не менял
- активная длина уменьшается
- активный краю смещается вправо (к первому символу следующего суффикса надо вставить)
Правило 2
если мы создадим новый внутренний узел или сделайте inserter от внутренний узел и это не первый такие внутренний узел на текущем шаге, то мы связываем предыдущий такие узел этой через суффикс ссылке.
данное определение Rule 2 отличается от jogojapan', так как здесь мы учитываем не только вновь созданный внутренние узлы, но и внутренние узлы, из которых мы делаем вставка.
Правило 3
после вставки из активный узел это не root узел, мы должны следовать ссылке суффикса и установить активный узел к узлу, на который он указывает. Если нет суффиксной ссылки, установите активный узел до root узел. В любом случае, активный краю и активная длина отдых не менявшийся.
в этом определении Rule 3 мы также рассматриваем вставки листовых узлов (не только сплит-узлов).
и, наконец, наблюдение 3:
когда символ, который мы хотим добавить к дереву, уже находится на краю, мы, согласно Observation 1 обновление только active point и remainder, оставив дерево без изменений. но если есть внутренний узел помечен как требуется суффикс ссылка, мы должны соединить этот узел с нашим текущим active node по суффиксной ссылке.
давайте рассмотрим пример дерева суффиксов для cdddcdc если мы добавим суффиксную ссылку в таком случае, и если мы этого не сделаем:
-
если мы НЕ соедините узлы через суффиксную ссылку:
- перед добавлением последней буквы c:
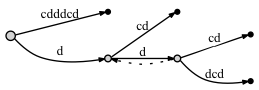
- после добавления последняя буква c:
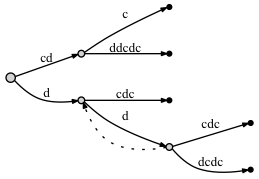
-
если мы DO соедините узлы через суффиксную ссылку:
- перед добавлением последней буквы c:
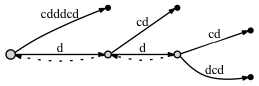
- после добавления последней буквы c:
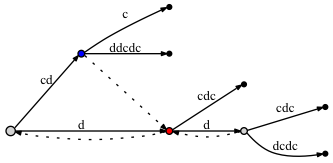
кажется, что нет существенной отличие: во втором случае есть еще две суффикс-ссылки. Но эти суффиксные ссылки являются правильно, и один из них - от синего узла до Красного-очень важно для нашего подхода с активные точки. Проблема в том, что если мы не поместим суффиксную ссылку здесь, позже, когда мы добавим некоторые новые буквы в дерево, мы можем опустить добавление некоторых узлов в дерево из-за Rule 3, потому что, согласно ему, если нет суффиксной ссылки, то мы должен поставить active_node в корень.
когда мы добавляли последнюю букву к дереву, Красный Узел имел существовала прежде чем мы сделали вставку из синего узла (край labled 'c'). Поскольку была вставка из синего узла, мы отмечаем ее как требуется суффикс ссылка. Тогда, полагаясь на активные точки подход active node был установлен в Красный Узел. Но мы не делаем вставку из красного узла, так как письмо!--17--> 'c' уже на краю. Означает ли это, что синий узел должен быть оставлен без суффиксной ссылки? Нет, мы должны соединить синий узел с красным через суффиксную ссылку. Почему это правильно? Потому что активные точки подход гарантирует, что мы попадем в нужное место, т. е. в следующее место, где мы должны обработать вставку короче суффиксом.
наконец, вот мои реализации суффикс Дерево:
надеюсь, что этот "обзор" в сочетании с подробным ответом jogojapan поможет кому-то реализовать свое собственное дерево суффиксов.
Спасибо за хорошо объясненный учебник по @jogojapan, я реализовал алгоритм в Python.
пара незначительных проблем, упомянутых @jogojapan, оказывается больше сложные чем я ожидал, и к нему нужно относиться очень осторожно. Это стоило мне нескольких дней, чтобы получить мою реализацию достаточно (Я полагаю). Проблемы и решения перечислены ниже:
конец с
Remainder > 0оказывается, эта ситуация также может произойти во время разворачивания шага, а не только конец всего алгоритма. Когда это произойдет, мы можем оставить остаток, actnode, actedge и actlength без изменений, завершите текущий шаг развертывания и начните другой шаг, либо продолжайте сворачивать или разворачивать в зависимости от того, находится ли следующий символ в исходной строке на текущем пути или нет.-
Прыжок Через Узлы: Когда мы следуем по ссылке суффикса, обновите активную точку, а затем обнаружите, что ее компонент active_length не работает хорошо с новым active_node. Мы должны!--2-->шаг вперед в нужное место, чтобы разделить или вставить лист. Этот процесс может быть не так просто потому что во время перемещения actlength и actedge постоянно меняются, когда вам нужно вернуться к корневой узел на actedge и actlength может быть неправильно из-за этих движений. Нам понадобится дополнительная переменная(ы), чтобы сохранить эту информацию.
две другие проблемы каким-то образом были указаны @managonov
Сплит Может Вырождаться при попытке разделить ребро, когда-нибудь вы обнаружите, что операция разделения находится прямо на узле. Этом случае нам нужно только добавить новый лист к этому узлу, берут это как стандартная операция разделения края, что означает, что суффиксные ссылки, если они есть, должны поддерживаться соответственно.
Скрытые Ссылки Суффикса есть еще один частный случай, который возникает 1 и 2. Иногда нам нужно перепрыгнуть через несколько узлов в нужную точку для split, мы могли бы перегнать правильная точка, если мы перемещаемся, сравнивая оставшуюся строку и метки пути. Что случай суффикс ссылка будет пренебрегаться непреднамеренно,если они должны быть. Этого можно было избежать запоминание правильной точки при движении вперед. Связь суффиксов должна поддерживаться, если разделенный узел уже существует или даже 1 происходит во время раскладывания шаг.
наконец, моя реализация в Python следующим образом:
советы: он включает в себя наивный печать дерево в коде выше, что очень важно при отладке. Он спас меня много время и удобно для обнаруживать местонахождение специальные случаи.
моя интуиция такова:
после K итераций основного цикла вы построили дерево суффиксов, которое содержит все суффиксы полной строки, которые начинаются с первых k символов.
в начале, это означает, что суффиксное дерево содержит один корневой узел, представляющий всю строку (это единственный суффикс, который начинается с 0).
после итераций LEN (string) у вас есть дерево суффиксов, которое содержит все суффиксы.
во время цикла ключ является активной точкой. Я предполагаю, что это самая глубокая точка в дереве суффиксов, которая соответствует правильному суффиксу первых k символов строки. (Я думаю, что правильный означает, что суффикс не может быть всей строкой.)
например, предположим, что вы видели символы 'abcabc'. Активная точка будет представлять собой точку в дереве, соответствующую суффиксу "abc".
активная точка представлен (origin, first, last). Это означает, что в данный момент Вы находитесь в точке дерева, которую вы получаете, начиная с начала узла, а затем вводя символы в строке[first:last]
когда вы добавляете новый символ, вы смотрите, находится ли активная точка в существующем дереве. Если это так, то с вами покончено. В противном случае вам нужно добавить новый узел в дерево суффиксов в активной точке, вернуться к следующему кратчайшему совпадению и проверить еще раз.
Примечание. Один: Указатели суффиксов дают ссылку на следующее кратчайшее совпадение для каждого узла.
примечание 2: При добавлении нового узла и резервного добавляется новый указатель суффикса для нового узла. Конечным пунктом для этого указателя суффикса будет узел в укороченной активной точке. Этот узел либо уже существует, либо будет создан на следующей итерации этого резервного цикла.
Примечание 3: часть канонизации просто сохраняет время в проверять активную точку. Например, предположим, что вы всегда используется origin=0 и просто изменяется первым и последним. Чтобы проверить активную точку, вам нужно будет каждый раз следовать дереву суффиксов вдоль всех промежуточных узлов. Имеет смысл кэшировать результаты по этому пути, записывая только расстояние от последнего узла.
можете ли вы привести пример кода того, что вы подразумеваете под "исправлением" ограничивающих переменных?
предупреждение о здоровье: я также нашел этот алгоритм особенно трудно понять, поэтому, пожалуйста, поймите, что эта интуиция вероятно, будут неверны во всех важных деталях...
Привет я попытался реализовать вышеописанную реализацию в ruby, пожалуйста, проверьте это. кажется, это работает нормально.
единственная разница в реализации заключается в том, что я попытался использовать объект edge вместо использования символов.
его на https://gist.github.com/suchitpuri/9304856
require 'pry'
class Edge
attr_accessor :data , :edges , :suffix_link
def initialize data
@data = data
@edges = []
@suffix_link = nil
end
def find_edge element
self.edges.each do |edge|
return edge if edge.data.start_with? element
end
return nil
end
end
class SuffixTrees
attr_accessor :root , :active_point , :remainder , :pending_prefixes , :last_split_edge , :remainder
def initialize
@root = Edge.new nil
@active_point = { active_node: @root , active_edge: nil , active_length: 0}
@remainder = 0
@pending_prefixes = []
@last_split_edge = nil
@remainder = 1
end
def build string
string.split("").each_with_index do |element , index|
add_to_edges @root , element
update_pending_prefix element
add_pending_elements_to_tree element
active_length = @active_point[:active_length]
# if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data[0..active_length-1] == @active_point[:active_edge].data[active_length..@active_point[:active_edge].data.length-1])
# @active_point[:active_edge].data = @active_point[:active_edge].data[0..active_length-1]
# @active_point[:active_edge].edges << Edge.new(@active_point[:active_edge].data)
# end
if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data.length == @active_point[:active_length] )
@active_point[:active_node] = @active_point[:active_edge]
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0])
@active_point[:active_length] = 0
end
end
end
def add_pending_elements_to_tree element
to_be_deleted = []
update_active_length = false
# binding.pry
if( @active_point[:active_node].find_edge(element[0]) != nil)
@active_point[:active_length] = @active_point[:active_length] + 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0]) if @active_point[:active_edge] == nil
@remainder = @remainder + 1
return
end
@pending_prefixes.each_with_index do |pending_prefix , index|
# binding.pry
if @active_point[:active_edge] == nil and @active_point[:active_node].find_edge(element[0]) == nil
@active_point[:active_node].edges << Edge.new(element)
else
@active_point[:active_edge] = node.find_edge(element[0]) if @active_point[:active_edge] == nil
data = @active_point[:active_edge].data
data = data.split("")
location = @active_point[:active_length]
# binding.pry
if(data[0..location].join == pending_prefix or @active_point[:active_node].find_edge(element) != nil )
else #tree split
split_edge data , index , element
end
end
end
end
def update_pending_prefix element
if @active_point[:active_edge] == nil
@pending_prefixes = [element]
return
end
@pending_prefixes = []
length = @active_point[:active_edge].data.length
data = @active_point[:active_edge].data
@remainder.times do |ctr|
@pending_prefixes << data[-(ctr+1)..data.length-1]
end
@pending_prefixes.reverse!
end
def split_edge data , index , element
location = @active_point[:active_length]
old_edges = []
internal_node = (@active_point[:active_edge].edges != nil)
if (internal_node)
old_edges = @active_point[:active_edge].edges
@active_point[:active_edge].edges = []
end
@active_point[:active_edge].data = data[0..location-1].join
@active_point[:active_edge].edges << Edge.new(data[location..data.size].join)
if internal_node
@active_point[:active_edge].edges << Edge.new(element)
else
@active_point[:active_edge].edges << Edge.new(data.last)
end
if internal_node
@active_point[:active_edge].edges[0].edges = old_edges
end
#setup the suffix link
if @last_split_edge != nil and @last_split_edge.data.end_with?@active_point[:active_edge].data
@last_split_edge.suffix_link = @active_point[:active_edge]
end
@last_split_edge = @active_point[:active_edge]
update_active_point index
end
def update_active_point index
if(@active_point[:active_node] == @root)
@active_point[:active_length] = @active_point[:active_length] - 1
@remainder = @remainder - 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(@pending_prefixes.first[index+1])
else
if @active_point[:active_node].suffix_link != nil
@active_point[:active_node] = @active_point[:active_node].suffix_link
else
@active_point[:active_node] = @root
end
@active_point[:active_edge] = @active_point[:active_node].find_edge(@active_point[:active_edge].data[0])
@remainder = @remainder - 1
end
end
def add_to_edges root , element
return if root == nil
root.data = root.data + element if(root.data and root.edges.size == 0)
root.edges.each do |edge|
add_to_edges edge , element
end
end
end
suffix_tree = SuffixTrees.new
suffix_tree.build("abcabxabcd")
binding.pry
@jogojapan вы принесли удивительное объяснение и визуализацию. Но, как отметил @makagonov, отсутствуют некоторые правила, касающиеся установки суффиксных ссылок. Это видно в хорошем смысле, когда идет шаг за шагом на http://brenden.github.io/ukkonen-animation/ через слово "aabaaabb". Когда вы переходите от шага 10 к шагу 11, нет суффиксной ссылки от узла 5 к узлу 2, но активная точка внезапно перемещается туда.
@makagonov так как я живу в мире Java, я также пытался следовать за вашим реализация для понимания рабочего процесса St building, но мне было трудно из-за:
- объединение ребер с узлами
- использование указателей индекса вместо ссылок
- разрывы заявления;
- продолжить высказывания;
таким образом, я закончил с такой реализацией на Java, которая, я надеюсь, отражает все шаги более ясным образом и сократит время обучения для других людей Java:
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class ST {
public class Node {
private final int id;
private final Map<Character, Edge> edges;
private Node slink;
public Node(final int id) {
this.id = id;
this.edges = new HashMap<>();
}
public void setSlink(final Node slink) {
this.slink = slink;
}
public Map<Character, Edge> getEdges() {
return this.edges;
}
public Node getSlink() {
return this.slink;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"id\"")
.append(":")
.append(this.id)
.append(",")
.append("\"slink\"")
.append(":")
.append(this.slink != null ? this.slink.id : null)
.append(",")
.append("\"edges\"")
.append(":")
.append(edgesToString(word))
.append("}")
.toString();
}
private StringBuilder edgesToString(final String word) {
final StringBuilder edgesStringBuilder = new StringBuilder();
edgesStringBuilder.append("{");
for(final Map.Entry<Character, Edge> entry : this.edges.entrySet()) {
edgesStringBuilder.append("\"")
.append(entry.getKey())
.append("\"")
.append(":")
.append(entry.getValue().toString(word))
.append(",");
}
if(!this.edges.isEmpty()) {
edgesStringBuilder.deleteCharAt(edgesStringBuilder.length() - 1);
}
edgesStringBuilder.append("}");
return edgesStringBuilder;
}
public boolean contains(final String word, final String suffix) {
return !suffix.isEmpty()
&& this.edges.containsKey(suffix.charAt(0))
&& this.edges.get(suffix.charAt(0)).contains(word, suffix);
}
}
public class Edge {
private final int from;
private final int to;
private final Node next;
public Edge(final int from, final int to, final Node next) {
this.from = from;
this.to = to;
this.next = next;
}
public int getFrom() {
return this.from;
}
public int getTo() {
return this.to;
}
public Node getNext() {
return this.next;
}
public int getLength() {
return this.to - this.from;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"content\"")
.append(":")
.append("\"")
.append(word.substring(this.from, this.to))
.append("\"")
.append(",")
.append("\"next\"")
.append(":")
.append(this.next != null ? this.next.toString(word) : null)
.append("}")
.toString();
}
public boolean contains(final String word, final String suffix) {
if(this.next == null) {
return word.substring(this.from, this.to).equals(suffix);
}
return suffix.startsWith(word.substring(this.from,
this.to)) && this.next.contains(word, suffix.substring(this.to - this.from));
}
}
public class ActivePoint {
private final Node activeNode;
private final Character activeEdgeFirstCharacter;
private final int activeLength;
public ActivePoint(final Node activeNode,
final Character activeEdgeFirstCharacter,
final int activeLength) {
this.activeNode = activeNode;
this.activeEdgeFirstCharacter = activeEdgeFirstCharacter;
this.activeLength = activeLength;
}
private Edge getActiveEdge() {
return this.activeNode.getEdges().get(this.activeEdgeFirstCharacter);
}
public boolean pointsToActiveNode() {
return this.activeLength == 0;
}
public boolean activeNodeIs(final Node node) {
return this.activeNode == node;
}
public boolean activeNodeHasEdgeStartingWith(final char character) {
return this.activeNode.getEdges().containsKey(character);
}
public boolean activeNodeHasSlink() {
return this.activeNode.getSlink() != null;
}
public boolean pointsToOnActiveEdge(final String word, final char character) {
return word.charAt(this.getActiveEdge().getFrom() + this.activeLength) == character;
}
public boolean pointsToTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() == this.activeLength;
}
public boolean pointsAfterTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() < this.activeLength;
}
public ActivePoint moveToEdgeStartingWithAndByOne(final char character) {
return new ActivePoint(this.activeNode, character, 1);
}
public ActivePoint moveToNextNodeOfActiveEdge() {
return new ActivePoint(this.getActiveEdge().getNext(), null, 0);
}
public ActivePoint moveToSlink() {
return new ActivePoint(this.activeNode.getSlink(),
this.activeEdgeFirstCharacter,
this.activeLength);
}
public ActivePoint moveTo(final Node node) {
return new ActivePoint(node, this.activeEdgeFirstCharacter, this.activeLength);
}
public ActivePoint moveByOneCharacter() {
return new ActivePoint(this.activeNode,
this.activeEdgeFirstCharacter,
this.activeLength + 1);
}
public ActivePoint moveToEdgeStartingWithAndByActiveLengthMinusOne(final Node node,
final char character) {
return new ActivePoint(node, character, this.activeLength - 1);
}
public ActivePoint moveToNextNodeOfActiveEdge(final String word, final int index) {
return new ActivePoint(this.getActiveEdge().getNext(),
word.charAt(index - this.activeLength + this.getActiveEdge().getLength()),
this.activeLength - this.getActiveEdge().getLength());
}
public void addEdgeToActiveNode(final char character, final Edge edge) {
this.activeNode.getEdges().put(character, edge);
}
public void splitActiveEdge(final String word,
final Node nodeToAdd,
final int index,
final char character) {
final Edge activeEdgeToSplit = this.getActiveEdge();
final Edge splittedEdge = new Edge(activeEdgeToSplit.getFrom(),
activeEdgeToSplit.getFrom() + this.activeLength,
nodeToAdd);
nodeToAdd.getEdges().put(word.charAt(activeEdgeToSplit.getFrom() + this.activeLength),
new Edge(activeEdgeToSplit.getFrom() + this.activeLength,
activeEdgeToSplit.getTo(),
activeEdgeToSplit.getNext()));
nodeToAdd.getEdges().put(character, new Edge(index, word.length(), null));
this.activeNode.getEdges().put(this.activeEdgeFirstCharacter, splittedEdge);
}
public Node setSlinkTo(final Node previouslyAddedNodeOrAddedEdgeNode,
final Node node) {
if(previouslyAddedNodeOrAddedEdgeNode != null) {
previouslyAddedNodeOrAddedEdgeNode.setSlink(node);
}
return node;
}
public Node setSlinkToActiveNode(final Node previouslyAddedNodeOrAddedEdgeNode) {
return setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, this.activeNode);
}
}
private static int idGenerator;
private final String word;
private final Node root;
private ActivePoint activePoint;
private int remainder;
public ST(final String word) {
this.word = word;
this.root = new Node(idGenerator++);
this.activePoint = new ActivePoint(this.root, null, 0);
this.remainder = 0;
build();
}
private void build() {
for(int i = 0; i < this.word.length(); i++) {
add(i, this.word.charAt(i));
}
}
private void add(final int index, final char character) {
this.remainder++;
boolean characterFoundInTheTree = false;
Node previouslyAddedNodeOrAddedEdgeNode = null;
while(!characterFoundInTheTree && this.remainder > 0) {
if(this.activePoint.pointsToActiveNode()) {
if(this.activePoint.activeNodeHasEdgeStartingWith(character)) {
activeNodeHasEdgeStartingWithCharacter(character, previouslyAddedNodeOrAddedEdgeNode);
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
rootNodeHasNotEdgeStartingWithCharacter(index, character);
}
else {
previouslyAddedNodeOrAddedEdgeNode = internalNodeHasNotEdgeStartingWithCharacter(index,
character, previouslyAddedNodeOrAddedEdgeNode);
}
}
}
else {
if(this.activePoint.pointsToOnActiveEdge(this.word, character)) {
activeEdgeHasCharacter();
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
previouslyAddedNodeOrAddedEdgeNode = edgeFromRootNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
else {
previouslyAddedNodeOrAddedEdgeNode = edgeFromInternalNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
}
}
}
}
private void activeNodeHasEdgeStartingWithCharacter(final char character,
final Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByOne(character);
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private void rootNodeHasNotEdgeStartingWithCharacter(final int index, final char character) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
this.activePoint = this.activePoint.moveTo(this.root);
this.remainder--;
assert this.remainder == 0;
}
private Node internalNodeHasNotEdgeStartingWithCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private void activeEdgeHasCharacter() {
this.activePoint = this.activePoint.moveByOneCharacter();
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private Node edgeFromRootNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByActiveLengthMinusOne(this.root,
this.word.charAt(index - this.remainder + 2));
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private Node edgeFromInternalNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private ActivePoint walkDown(final int index) {
while(!this.activePoint.pointsToActiveNode()
&& (this.activePoint.pointsToTheEndOfActiveEdge() || this.activePoint.pointsAfterTheEndOfActiveEdge())) {
if(this.activePoint.pointsAfterTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge(this.word, index);
}
else {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
return this.activePoint;
}
public String toString(final String word) {
return this.root.toString(word);
}
public boolean contains(final String suffix) {
return this.root.contains(this.word, suffix);
}
public static void main(final String[] args) {
final String[] words = {
"abcabcabc$",
"abc$",
"abcabxabcd$",
"abcabxabda$",
"abcabxad$",
"aabaaabb$",
"aababcabcd$",
"ababcabcd$",
"abccba$",
"mississipi$",
"abacabadabacabae$",
"abcabcd$",
"00132220$"
};
Arrays.stream(words).forEach(word -> {
System.out.println("Building suffix tree for word: " + word);
final ST suffixTree = new ST(word);
System.out.println("Suffix tree: " + suffixTree.toString(word));
for(int i = 0; i < word.length() - 1; i++) {
assert suffixTree.contains(word.substring(i)) : word.substring(i);
}
});
}
}
