Алгоритм максимизации покрытия прямоугольной области масштабирующими плитками
Я N масштабируемые квадратные плитки (кнопки), которые должны быть размещены внутри прямоугольной поверхности фиксированного размера (toolbox). Я хотел бы представить кнопки всех одинакового размера.
как я могу решить для оптимального размера плиток, которые обеспечат наибольшую площадь прямоугольной поверхности, покрытой плитками.
7 ответов
пусть W и H - ширина и высота прямоугольника.
пусть s длина стороны квадрата.
тогда количество квадратов n(s) что вы можете поместиться в прямоугольник floor(W/s)*floor(H/s). Вы хотите найти максимальное значение s для чего n(s) >= N
если вы построите квадраты против s вы получите кусочно-постоянная функция. Разрывы находятся на значениях W/i и H/j, где i и j выполнить через положительные целые числа.
вы хотите найти самый маленький i для чего n(W/i) >= N, а так же самый маленький j для чего n(H/j) >= N. Назовите эти наименьшие значения i_min и j_min. Тогда самый большой из W/i_min и H/j_min - это s что вы хотите.
то есть. s_max = max(W/i_min,H/j_min)
найти i_min и j_min, просто выполните поиск грубой силы:для каждого, начните с 1, проверьте и увеличьте.
в случае, если N очень большой, может быть неприятно искать iи jначинается с 1 (хотя трудно представить, что будет какая-либо заметная разница в производительности). В этом случае, мы можем оценить начальные значения следующим образом. Во-первых, приблизительная оценка площади плитки W*H/N, соответствующий стороне sqrt(W*H/N). Если W/i <= sqrt(W*H/N), потом i >= ceil(W*sqrt(N/(W*H))) аналогично j >= ceil(H*sqrt(N/(W*H)))
Итак, вместо того, чтобы начинать петли на i=1 и j=1, мы можем начать их на i = ceil(sqrt(N*W/H)) и j = ceil(sqrt(N*H/W))). И ОП предполагает, что round работает лучше, чем ceil -- в худшем случае дополнительная итерация.
вот алгоритм, написанный на C++:
#include <math.h>
#include <algorithm>
// find optimal (largest) tile size for which
// at least N tiles fit in WxH rectangle
double optimal_size (double W, double H, int N)
{
int i_min, j_min ; // minimum values for which you get at least N tiles
for (int i=round(sqrt(N*W/H)) ; ; i++) {
if (i*floor(H*i/W) >= N) {
i_min = i ;
break ;
}
}
for (int j=round(sqrt(N*H/W)) ; ; j++) {
if (floor(W*j/H)*j >= N) {
j_min = j ;
break ;
}
}
return std::max (W/i_min, H/j_min) ;
}
выше написано для наглядности. Код может быть значительно ужесточен следующим образом:
double optimal_size (double W, double H, int N)
{
int i,j ;
for (i = round(sqrt(N*W/H)) ; i*floor(H*i/W) < N ; i++){}
for (j = round(sqrt(N*H/W)) ; floor(W*j/H)*j < N ; j++){}
return std::max (W/i, H/j) ;
}
Я считаю, что это можно решить как ограниченную задачу минимизации, которая требует некоторого базового исчисления. .
определение:
a, l -> rectangle sides
k -> number of squares
s -> side of the squares
вы должны минимизировать функцию:
f[s]:= a * l/s^2 - k
при ограничениях:
IntegerPart[a/s] IntegerPart[l/s] - k >= 0
s > 0
я запрограммировал небольшую функцию Mathematica, чтобы сделать трюк
f[a_, l_, k_] := NMinimize[{a l/s^2 - k ,
IntegerPart[a/s] IntegerPart[l/s] - k >= 0,
s > 0},
{s}]
легко читается, так как уравнения такие же, как и выше.
используя эту функцию, я составил таблицу для выделение 6 площади
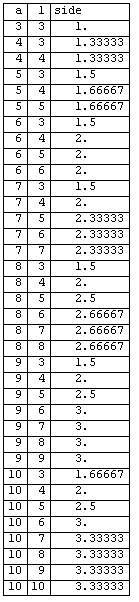
насколько я вижу, результаты верны.
как я уже сказал, Вы можете использовать стандартный пакет исчисления для своей среды, или вы также можете разработать свой собственный алгоритм минимизации и программы. Позвоните в колокол, если вы решите для последнего варианта, и я предоставлю несколько хороших указателей.
HTH!
редактировать
просто для удовольствия, я сделал сюжет с результаты.
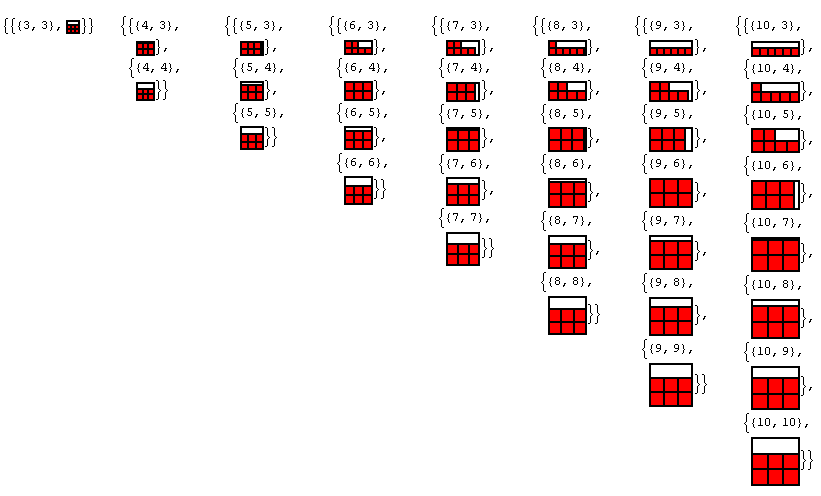
и для 31 плитки:
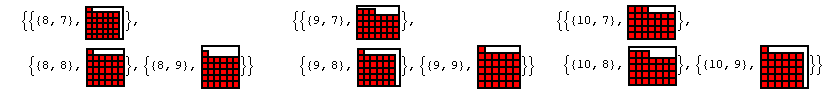
Edit 2: Характерные Параметры
задача имеет три характерных параметра:
- результирующий размер плитки
- количество плиток
- отношение l / a заключительного прямоугольника
возможно, последний может привести к несколько удивительным, но это легко поймите: если у вас есть проблема с прямоугольником 7x5 и 6 плитками для размещения, глядя в приведенную выше таблицу, размер квадратов будет 2.33. Теперь, если у вас есть прямоугольник 70x50, очевидно, что результирующие плитки будут 23.33, масштабирование изометрически с проблемой.
Итак, мы можем взять эти три параметра и построить 3D-график их взаимосвязи и в конечном итоге сопоставить кривую с некоторой функцией, которую легче вычислить (используя, например, наименьшие квадраты или вычисляя iso-значение регионы.)
в любом случае, результирующий масштабированный участок:
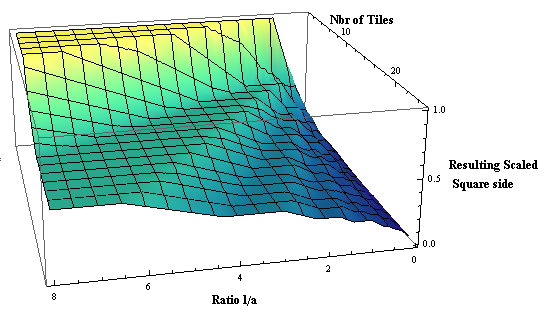
Я понимаю, что это старый нить, но я недавно решил эту проблему таким образом, что я думаю, эффективна и всегда дает правильный ответ. Он предназначен для поддержания заданного соотношения сторон. Если вы хотите, чтобы дети (кнопки в этом случае) были квадратными, просто используйте соотношение сторон 1. В настоящее время я использую этот алгоритм в нескольких местах, и он отлично работает.
double VerticalScale; // for the vertical scalar: uses the lowbound number of columns
double HorizontalScale;// horizontal scalar: uses the highbound number of columns
double numColumns; // the exact number of columns that would maximize area
double highNumRows; // number of rows calculated using the upper bound columns
double lowNumRows; // number of rows calculated using the lower bound columns
double lowBoundColumns; // floor value of the estimated number of columns found
double highBoundColumns; // ceiling value of the the estimated number of columns found
Size rectangleSize = new Size(); // rectangle size will be used as a default value that is the exact aspect ratio desired.
//
// Aspect Ratio = h / w
// where h is the height of the child and w is the width
//
// the numerator will be the aspect ratio and the denominator will always be one
// if you want it to be square just use an aspect ratio of 1
rectangleSize.Width = desiredAspectRatio;
rectangleSize.Height = 1;
// estimate of the number of columns useing the formula:
// n * W * h
// columns = SquareRoot( ------------- )
// H * w
//
// Where n is the number of items, W is the width of the parent, H is the height of the parent,
// h is the height of the child, and w is the width of the child
numColumns = Math.Sqrt( (numRectangles * rectangleSize.Height * parentSize.Width) / (parentSize.Height * rectangleSize.Width) );
lowBoundColumns = Math.Floor(numColumns);
highBoundColumns = Math.Ceiling(numColumns);
// The number of rows is determined by finding the floor of the number of children divided by the columns
lowNumRows = Math.Ceiling(numRectangles / lowBoundColumns);
highNumRows = Math.Ceiling(numRectangles / highBoundColumns);
// Vertical Scale is what you multiply the vertical size of the child to find the expected area if you were to find
// the size of the rectangle by maximizing by rows
//
// H
// Vertical Scale = ----------
// R * h
//
// Where H is the height of the parent, R is the number of rows, and h is the height of the child
//
VerticalScale = parentSize.Height / lowNumRows * rectangleSize.Height;
//Horizontal Scale is what you multiply the horizintale size of the child to find the expected area if you were to find
// the size of the rectangle by maximizing by columns
//
// W
// Vertical Scale = ----------
// c * w
//
//Where W is the width of the parent, c is the number of columns, and w is the width of the child
HorizontalScale = parentSize.Width / (highBoundColumns * rectangleSize.Width);
// The Max areas are what is used to determine if we should maximize over rows or columns
// The areas are found by multiplying the scale by the appropriate height or width and finding the area after the scale
//
// Horizontal Area = Sh * w * ( (Sh * w) / A )
//
// where Sh is the horizontal scale, w is the width of the child, and A is the aspect ratio of the child
//
double MaxHorizontalArea = (HorizontalScale * rectangleSize.Width) * ((HorizontalScale * rectangleSize.Width) / desiredAspectRatio);
//
//
// Vertical Area = Sv * h * (Sv * h) * A
// Where Sv isthe vertical scale, h is the height of the child, and A is the aspect ratio of the child
//
double MaxVerticalArea = (VerticalScale * rectangleSize.Height) * ((VerticalScale * rectangleSize.Height) * desiredAspectRatio);
if (MaxHorizontalArea >= MaxVerticalArea ) // the horizontal are is greater than the max area then we maximize by columns
{
// the width is determined by dividing the parent's width by the estimated number of columns
// this calculation will work for NEARLY all of the horizontal cases with only a few exceptions
newSize.Width = parentSize.Width / highBoundColumns; // we use highBoundColumns because that's what is used for the Horizontal
newSize.Height = newSize.Width / desiredAspectRatio; // A = w/h or h= w/A
// In the cases that is doesnt work it is because the height of the new items is greater than the
// height of the parents. this only happens when transitioning to putting all the objects into
// only one row
if (newSize.Height * Math.Ceiling(numRectangles / highBoundColumns) > parentSize.Height)
{
//in this case the best solution is usually to maximize by rows instead
double newHeight = parentSize.Height / highNumRows;
double newWidth = newHeight * desiredAspectRatio;
// However this doesn't always work because in one specific case the number of rows is more than actually needed
// and the width of the objects end up being smaller than the size of the parent because we don't have enough
// columns
if (newWidth * numRectangles < parentSize.Width)
{
//When this is the case the best idea is to maximize over columns again but increment the columns by one
//This takes care of it for most cases for when this happens.
newWidth = parentSize.Width / Math.Ceiling(numColumns++);
newHeight = newWidth / desiredAspectRatio;
// in order to make sure the rectangles don't go over bounds we
// increment the number of columns until it is under bounds again.
while (newWidth * numRectangles > parentSize.Width)
{
newWidth = parentSize.Width / Math.Ceiling(numColumns++);
newHeight = newWidth / desiredAspectRatio;
}
// however after doing this it is possible to have the height too small.
// this will only happen if there is one row of objects. so the solution is to make the objects'
// height equal to the height of their parent
if (newHeight > parentSize.Height)
{
newHeight = parentSize.Height;
newWidth = newHeight * desiredAspectRatio;
}
}
// if we have a lot of added items occaisionally the previous checks will come very close to maximizing both columns and rows
// what happens in this case is that neither end up maximized
// because we don't know what set of rows and columns were used to get us to where we are
// we must recalculate them with the current measurements
double currentCols = Math.Floor(parentSize.Width / newWidth);
double currentRows = Math.Ceiling(numRectangles/currentCols);
// now we check and see if neither the rows or columns are maximized
if ( (newWidth * currentCols ) < parentSize.Width && ( newHeight * Math.Ceiling(numRectangles/currentCols) ) < parentSize.Height)
{
// maximize by columns first
newWidth = parentSize.Width / currentCols;
newHeight = newSize.Width / desiredAspectRatio;
// if the columns are over their bounds, then maximized by the columns instead
if (newHeight * Math.Ceiling(numRectangles / currentCols) > parentSize.Height)
{
newHeight = parentSize.Height / currentRows;
newWidth = newHeight * desiredAspectRatio;
}
}
// finally we have the height of the objects as maximized using columns
newSize.Height = newHeight;
newSize.Width = newWidth;
}
}
else
{
//Here we use the vertical scale. We determine the height of the objects based upong
// the estimated number of rows.
// This work for all known cases
newSize.Height = parentSize.Height / lowNumRows;
newSize.Width = newSize.Height * desiredAspectRatio;
}
в конце алгоритма 'newSize' имеет соответствующий размер. Это написано на C#, но это будет довольно легко переносится на другие языки.
первая, очень грубая эвристика-взять
s = floor( sqrt( (X x Y) / N) )
здесь s это кнопка-сторона-длина,X и Y являются ширина и высота панели инструментов, и N - это количество кнопок.
в этом случае s будет максимально возможной длиной стороны. Однако этот набор кнопок не обязательно можно отобразить на панели инструментов.
представьте себе панель инструментов, которая составляет 20 единиц на 1 единицу с 5 кнопками. Эвристика даст вам длина одной стороны 2 (зона 4), общей площадью 20. Однако половина каждой кнопки будет находиться за пределами панели инструментов.
Я бы взял итеративный подход здесь. Я бы проверил, можно ли поместить все кнопки в одну строку. Если нет, проверьте, можно ли поместиться в два ряда, и так далее.
скажем, W-меньшая сторона панели инструментов. H-это другая сторона.
для каждой итерации я бы проверил лучшие и худшие возможные случаи в этом порядке. В лучшем случае означает, скажем, что это N-я итерация, попробует размер кнопок W/n X W/n. Если значение h достаточно, тогда мы закончили. Если нет, то худший случай-попробовать(W/(n+1))+1 x(W/(n+1))+1 кнопки размера. Если можно поместить все кнопки, то я бы попробовал метод деления между W/n и (W / (n+1))+1. Если не итерация продолжается при n+1.
пусть n (s) - количество квадратов, которые могут поместиться и S их сторона. Пусть W, H-стороны прямоугольника для заполнения. Тогда n(s) = этаж(Вт/с)* этаж (ч/с). Это монотонно убывающая функция в s, а также кусочно-постоянная, поэтому вы можете выполнить небольшую модификацию двоичного поиска, чтобы найти наименьший s такой, что n(s) >= N, но n(s+eps) = N тогда l = min (W / floor(W/t), H/floor(H/t)) в противном случае u = max(W/floor(W/t), H/floor (H/t)). Остановитесь, когда u и l остаются одинаковыми в последовательных итерациях. Это похоже на двоичный поиск, но вы используете тот факт, что функция кусочно-постоянная, а точки изменения-когда W или H являются точными кратными s. Хорошая маленькая проблема, спасибо, что предложил.
мы знаем, что любое оптимальное решение (может быть два) заполнит прямоугольник по горизонтали или по вертикали. Если вы нашли оптимальное решение, которое не заполняло прямоугольник в одном измерении, вы всегда можете увеличить масштаб плиток для заполнения одного измерения.
теперь любое решение, которое максимизирует покрытую поверхность, будет иметь соотношение сторон, близкое к соотношению сторон прямоугольника. Соотношение сторон решения vertical tile count/horizontal tile count (и соотношение сторон прямоугольник Y/X).
вы можете упростить задачу, заставляя Y>=X; другими словами, если X>Y, транспонировать прямоугольника. Это позволяет вам думать только о соотношениях сторон >= 1, пока вы не забудете перенести решение обратно.
после того как вы рассчитали пропорции, вы хотите найти решения проблемы V/H ~= Y/X, где V является количество вертикальных плиток и H горизонтальный отсчет плитки. Вы найдете до трех решений: ближайший V/H to Y/X и V+1, V-1. В этот момент просто вычислите покрытие на основе шкалы, используя V и H и возьмите максимум (может быть более одного).
