Алгоритм нахождения наименьшего количества прямоугольников для покрытия набора прямоугольников без перекрытия
У меня есть набор прямоугольников, и я хотел бы "уменьшить" набор, чтобы у меня было наименьшее количество прямоугольников для описания той же области, что и исходный набор. Если возможно, я хотел бы, чтобы это было быстро, но я больше озабочен тем, чтобы как можно меньше прямоугольников. У меня есть подход, который работает большую часть времени.
В настоящее время я начинаю с самого верхнего левого прямоугольника и вижу, могу ли я развернуть его вправо и вниз, сохраняя при этом прямоугольник. Я делаю это пока он не сможет больше расширяться, удалите и разделите все пересекающиеся прямоугольники и добавьте развернутый прямоугольник обратно в список. Затем я снова начинаю процесс со следующего левого верхнего прямоугольника и так далее. Но в некоторых случаях это не работает. Например:

с этим набором из трех прямоугольников правильное решение будет заканчиваться двумя прямоугольниками, как это:

однако в этом случае мой алгоритм начинается с обработки синего прямоугольника. Это расширение вниз и разбивает желтый прямоугольник (правильно). Но затем, когда остаток желтого прямоугольника обрабатывается, вместо того, чтобы расширяться вниз, он сначала расширяется вправо и забирает часть, которая была ранее отделена. Затем обрабатывается последний прямоугольник, и он не может расширяться вправо или вниз, поэтому исходный набор прямоугольников остается. Я мог бы настроить алгоритм, чтобы сначала развернуть его вниз, а затем вправо. Это исправит этот случай, но это вызовет ту же проблему в аналогичном сценарии это было отражено.
Edit: чтобы уточнить, исходный набор прямоугольников не перекрывается и не должен быть подключен. И если подмножество прямоугольников связано, полигон, который полностью их покрывает, может иметь в нем отверстия.
2 ответов
несмотря на название вашего вопроса, я думаю, что вы на самом деле ищете минимум рассечение в прямоугольники прямолинейного многоугольника. (Ссылки Джейсона о минимуме крышки прямоугольниками, что является совсем другой проблемой.)
Дэвид Эпштайна Расположе обсуждает эту проблему в разделе 3 его статьи обследования 2010 теоретико-графовые решения задач вычислительной геометрии, и он дает хорошее резюме в этот ответ на mathoverflow.net:
идея в том, чтобы найти максимальное количество оси-параллельными непересекающимися диагоналями двух вогнутых вершин на концах, разделенный вдоль, и затем еще один сплит для каждого оставшегося вогнутой вершиной. Чтобы найти максимальное число осей-параллельных непересекающихся диагоналей, форма графика пересечения диагоналей; этот граф-двудольный, поэтому его максимальном независимом множестве можно найти за полиномиальное время по паросочетание методы.
вот мой глянец на это восхитительно краткое описание, используя Рисунок 2 из статьи Эппштейна. Предположим, у нас есть прямолинейный многоугольник, возможно, с отверстиями.
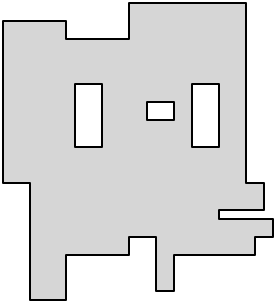
когда многоугольник рассечен на прямоугольники, каждая из вогнутых вершин должна быть встречена хотя бы одним краем рассечения. Итак, мы получаем минимум препарирование если как можно больше из этих краев делают двойн-обязанность, то есть, они соединяют 2 из вогнутые вершины.
Итак, давайте нарисуем параллельные оси диагонали между двумя вогнутыми вершинами, которые содержатся полностью внутри многоугольника. ("Ось-параллель "означает" горизонтальная или вертикальная " здесь и диагональ многоугольника - линия, соединяющая две несмежные вершины.) Мы хотим использовать как можно больше этих линий в рассечении, пока они не пересекаются.
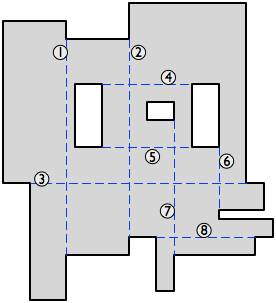
(Если нет диагоналей, параллельных оси, то рассечение тривиально-просто сделайте разрез из каждой вогнутой вершины. Или, если нет пересечений между диагоналями, параллельными оси, мы используем их все, плюс разрез от каждой оставшейся вогнутой вершины. В противном случае, читайте дальше.)
на график перекрестке из набора сегментов линии имеет узел для каждого сегмента линии, и ребро соединяет два узла, если линии пересекаются. Вот график пересечения для оси-параллели диагонали:
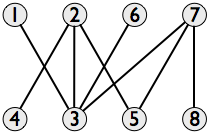
Это двудольные с вертикальными диагоналями в одной части и горизонтальными диагоналями в другой части. Теперь мы хотим выбрать как можно больше диагоналей, пока они не пересекаются. Это соответствует поиску максимальный независимый набор на графике пересечения.
нахождение максимального независимого множества В общем графе является NP-трудной задачей, но в частном случае двудольный граф, теорема Кенига показывает, что это эквивалентно задаче поиска максимального соответствия, которая может быть решена в полиномиальное время, например, с помощью алгоритм Хопкрофта–карпа. Данный график может иметь несколько максимальных соответствий, но любой из них будет делать, так как все они имеют одинаковый размер. В Примере все максимально сравнения имеют три пары вершин, например {(2, 4), (6, 3), (7, 8)}:
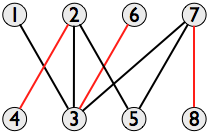
(другие максимальные совпадения на этом графике включают {(1, 3), (2, 5), (7, 8)}; {(2, 4), (3, 6), (5, 7)}; и {(1, 3), (2, 4), (7, 8)}.)
чтобы получить от максимального соответствия соответствующему минимального вершинного покрытия применить доказательство теоремы Кенига. В соответствии, показанном выше, левый набор L = {1, 2, 6, 7}, правильный набор является R = {3, 4, 5, 8}, и набор непревзойденных вершин в L и U = {1}. Существует только один переменный путь, начинающийся в U, а именно 1-3-6, поэтому множество вершин в чередующихся путей Z = {1, 3, 6} и, таким образом, минимальное покрытие вершины K = (L \ Z) ∪ (R ∩ Z) = {2, 3, 7}, показано красным цветом ниже, с максимальным независимым набором в зеленом:

переводя это обратно в проблему рассечения, это означает, что мы можем использовать пять оси - параллельные диагонали в разрезе:
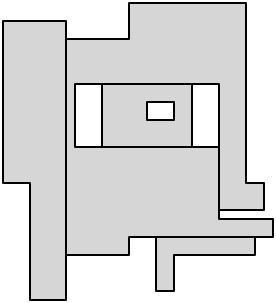
наконец, сделайте разрез из каждой оставшейся вогнутой вершины, чтобы завершить рассечение:
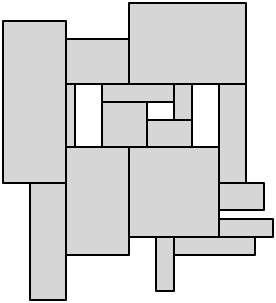
вот некоторые научные статьи, обсуждающие решения этой проблемы;
алгоритм линейно-временной аппроксимации для минимального прямоугольного покрытия (это для покрытия полигонов, поэтому это более общий случай, чем то, что вы представили здесь).
оптимальная прямоугольная форма крышки выпуклая Rectinlinear полигоны (это один больше по линиям вашей конкретной проблемы)
вы также можете попробовать здесь для a библиография других работ на эту тему.
