использование RPN (обратная польская нотация)

для введения RPN см. здесь.

проблема в размере

мы должны построить список из четырех чисел, который подразумевает 3 оператора.
Эти числа и операторы будут выталкиваться или выполняться против стека.

вызовем список выполнения {a1 a2 a3 a4 a5 a6 a7}.

{a1 a2} должны быть числами, так как их нет унарные операции в стеке.

{a7} должен быть оператором, чтобы завершить операцию.

для {a3, a4, a5, a6} у нас есть несколько вариантов, но всегда по крайней мере два числа должны быть в стеке, чтобы иметь возможность работать. Таким образом, возможные комбинации: (N= число, o=оператор)

{N N O O}, {N O N O}, {O N O N}, {O N N O} и {N O N}.

комбинация {O O N n} запрещена, потому что стек пуст для второго О.

Итак, мы имеем:

      | {N N O O} |  
      | {N O N O} |  
{N N} | {O N O N} | {O}  
      | {O N N O} |  
      | {N O O N} |  

теперь мы будем считать возможные договоренности. Конечно, мы пересчитываем, потому что коммутативный оператор (Плюс и раз) может разрезать дерево перестановок пополам, но проблема достаточно мала, чтобы не беспокоиться об этом. (Мы также преодолеваем в тех случаях, когда последовательность {O o}. но мы просто идем дальше ..)

мы должны выбрать 2 номера в четырех для первого сегмента, это 12 возможные механизмы.

для среднего сегмента два оставшихся числа могут быть только перестановочными, то есть коэффициент 2

но у нас есть еще один фактор 5 для подсчета пяти альтернатив для среднего сегмента.

для трех операторов, как они могут повторить, у нас есть фактор 4^3=64

таким образом, размер проблемы является произведением чисел полужирным шрифтом: 12 2 5 64 = 7680. Никакой оптимизации не требуется, мы можем идти вперед грубой силой.

остальная часть проблемы заключается в создании механизмов 7680 и оценщика RPN. Обе относительно легкие задачи.

я опубликую его ...это все еще черновик, но здесь слишком поздно! Последует завтра!

Edit: RPN Evaluator

вот код для рекурсивного вычислителя RPN. Я решаю сделать это на функциональном языке (Mathematica) для упрощения синтаксического анализа оператора

rpn[listipt_, stackipt_: {}] := 
  Module[{list=listipt,stack=stackipt}, (*recursive rpn evaluator*)

    If[list == {}, Return[stack[[1]]]];        (*end*)
    If[NumberQ[list[[1]]],                     (*if numeric*)
     Return@rpn[Rest[list], PrependTo[stack,list[[1]]]];  (*push nbr and recurse*)
    ,
     (stack[[2]]=list[[1]][stack[[2]], stack[[1]]];       (*if not, operate*)
      Return@rpn[Rest[list], Rest[stack]];);              (*and recurse*)
   ];
];

пример использования

rpn[{1, 1, 1, Plus, Plus}]
3

rpn[{2, 2, 2, Plus, Plus}]
6

rpn[{2, 3, 4, Plus, Times}]  (* (4+3)*7 *)
14

rpn[{2, 3, 4, Plus, Divide}]  (* (2+3)/4 *)
2/7  

немного позже я опубликую генератор кортежей, покажу, что они 7680 и некоторые забавные результаты о распределении возможных результатов операций (на самом деле для набора {1,2,3,4} вы можете получить только 230 разных результатов!).

Edit: кортежи строительство

Сначала мы явно построим возможности для середины сегмент

t1 = {{n3, n4, o1, o2}, 
      {n3, o1, n4, o2}, 
      {o1, n3, o2, n4}, 
      {o1, n3, n4, o2}, 
      {n3, o1, o2, n4}};

теперь мы добавим два варианта для {n1,n2} и последнего оператора

t2 = Join[Map[Join[{n1, n2}, #, {o3}] &, t1], 
          Map[Join[{n2, n1}, #, {o3}] &, t1]] ( bahh ... don't mind the code*)

Приводящ в наших 10 различных конфигурациях

теперь мы должны заполнить все эти конфигурации всеми возможными перестановками чисел и операторов.

сначала мы строим все перестановки чисел как правила присвоения для наших кортежей

 repListNumbers = (*construct all number permutations*)
    Table[{n1 -> #[[1]], n2 -> #[[2]], n3 -> #[[3]], n4 -> #[[4]]} &[i], 
         {i, Permutations[{1, 2, 3, 4}]}];

эти маленькие зверьки имеют форма

  {n1 -> 1, n2 -> 2, n3 -> 3, n4 -> 4}

и мы можем использовать их для замены валлю в наших кортежах. Например:

  {n1,n2,n3,o1,o2,n4,o3} /. {n1 -> 1, n2 -> 2, n3 -> 3, n4 -> 4}

результаты

  {1,2,3,o1,o2,4,o3}

конечно, мы, возможно, построили правила замены как функцию, чтобы иметь возможность изменять набор чисел по желанию. Мы делаем сейчас нечто подобное с операторами

repListOps =      (*Construct all possible 3 element tuples*)
  Table[{o1 -> #[[1]], o2 -> #[[2]], o3 -> #[[3]]} &[i], 
      {i, Tuples[{Plus, Times, Divide, Subtract}, 3]}];    

таким образом, мы получаем коллекцию таких вещей, как

 {o1->Plus, o2->Plus, o3->Divide}

теперь мы совмещаем наши кортежи и все наши правила замены в одном большом список:

t3 = Flatten[t2 /. repListNumbers /. repListOps, 2];

что приводит к 15360 различным вычислениям. Но мы знаем, что там пересчитано в два раза, поэтому теперь отбрасываем повторяющиеся элементы:

t3 =Union[t3]

и это дает нам наши ожидаемые 7680 элементы.

есть еще некоторое перерасчет, потому что {2,3, Times} = {3,2, Times} = 6, но это нормально для наших текущих целей.

оценка результатов

теперь у нас есть наш оценщик RPN и все эти кортежи, и мы хотим знать, возможен ли определенный конечный результат.

мы просто должны спросить, содержится ли это число в наборе результатов:

In[252]:= MemberQ[rpn /@ t3, 24]
Out[252]= True

In[253]:= MemberQ[rpn /@ t3, 38]
Out[253]= False

фактически границами для результирующего набора являются:

In[254]:= Max[rpn /@ t3]
Out[254]= Max[36, ComplexInfinity]

In[255]:= Min[rpn /@ t3]
Out[255]= Min[-23, ComplexInfinity]

результаты бесконечности обусловлены тем, что меня не волновали деления на ноль, поэтому они есть , только внутри множества. Числовой интервал [-23,36].

если вы хотите знать, сколько результатов равны 24, просто посчитайте их

      In[259]:= Length@Select[t3, rpn[#] == 24 &]
      Out[259]= 484

конечно, многие из них являются тривиальными перестановками из-за коммутативных свойств "Плюс" и "раз", но не все:

   {1, 2, Plus, 3, Plus, 4, Times}      -> ((1+2)+3)*4  = 24
   {2, 1, 4, 3, Times, Divide, Divide}  ->  2/(1/(4*3)) = 24

нет последовательности, использующей "вычесть", которая дает 24!

    In[260]:= MemberQ[Flatten@Select[t3, rpn[#] == 24 &], Subtract]
    Out[260]= False

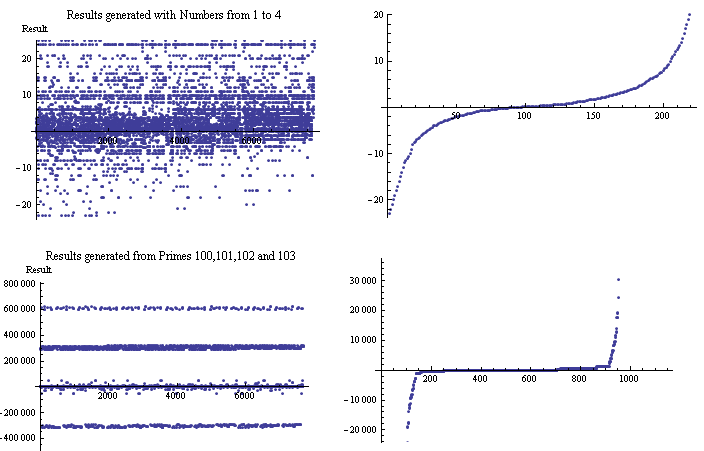
результаты выборочного спектра