Алгоритм покрытия максимального числа точек одной окружностью заданного радиуса

Это "проблема частичного покрытия диска" в литературе-это должно дать вам хорошее место, чтобы начать гуглить. Вот бумага, охватывающая одно возможное решение, но она немного интенсивна математически:http://www.utdallas.edu / ~edsha / papers/bin / ISPAN04_cover.pdf

на самом деле, это относится к области, называемой вычислительной геометрией, которая увлекательна, но может быть трудно зацепиться. Хороший обзор deBerg на различных алгоритмы, связанные с предметом.

Если вы хотите что-то простое, возьмите случайную позицию (x,y), вычислите количество точек внутри круга и сравните с предыдущей позицией. Бери максимум. Повторите операцию в любое время.

Почему, черт возьми, downvote? Когда-нибудь слышали о методах Монте-Карло? На самом деле для огромного количества точек детерминированный алгоритм может не закончиться в разумное время.

проблема возвращается к поиску глобальные оптимум функции f :R x R -> N. Входные данные для f является центральной точкой круга, а значение, конечно же, является количеством включенных точек из набора. График функции будет прерывистым, лестничным.

вы можете начать с тестирования функции в каждой точке, соответствующей точке в наборе, упорядочить точки, уменьшив значения f, затем активизируйте поиск вокруг этих точек (например, двигаясь по спирали).

другой вариант рассмотреть все точки пересечения сегментов, соединяющих любые пары точек в наборе. Ваш оптимальный точка будет на одном из этих перекрестков, я думаю, но их количество, вероятно, слишком велико, чтобы рассмотреть.

вы также можете гибридизировать варианты 1 и 2 и рассматривать пересечения сегментов, генерируемых из точек вокруг " хорошего набора точки.'

во всяком случае, если количество заданных точек не низкое (что позволяет проверить все пересечения), я не думаю вы можете гарантировать, чтобы найти оптимальную (просто хорошее решение).

на первый взгляд, я бы сказал, что решение quad tree.

кроме того, существует метод визуализации информации / интеллектуального анализа данных под названием K-means, который создает кластеры данных. Его можно использовать с добавленной функциональностью в конце, чтобы соответствовать вашей цели.

основной алгоритм для K-средних:

1. поместите K точек в пространство, представленное элементами которые кластеризуются - эти точки представляют собой начальную группу центроиды!--8-->
2. назначьте каждый элемент данных группе, которая имеет ближайший центроид
3. когда все элементы были назначены, пересчитайте позиции K центроидов путем вычисления среднего положения ваших точек
4. повторите шаги 2 и 3, пока центроиды не перестанут двигаться или двигаться очень мало

добавленная функциональность будет тогда:

1. вычислить количество точек в пределах вашего круга, расположенных на K центроиды!--8-->
2. выберите тот, что подходит вам лучше всего ;)

источники:
K-означает алгоритм -Университет Линчепинга
Quadtree -en.wikipedia.org/wiki/Quadtree

быстрый поиск в Википедии, и вы найдете исходный код:en.wikipedia.org/wiki/K-means_clustering

вот две идеи: алгоритм аппроксимации O(n) и точный(не приближенный) алгоритм O (n^2 log n):

быстрое приближение

используйте хэширование с учетом местоположения. В принципе, хэш каждой точки в хэш-ведро, которое содержит все близлежащие точки. Ведра настроены так, что столкновения происходят только между соседними точками - в отличие от одноименных хэш-таблиц, столкновения полезны здесь. Подсчет количества столкновений в ведре, а затем используйте центр этого ведра как центр вашего круга.

Я признаю, что это быстрое объяснение концепции, которая не является супер-очевидной в первый раз, когда вы слышите об этом. Аналогией было бы спросить группу людей, что такое их почтовый индекс, и использовать наиболее распространенный почтовый индекс для определения наиболее густонаселенного круга. Это не идеально, но хорошая быстрая эвристика.

Это в основном линейное время с точки зрения количества точек, и вы можете обновить свой набор данных на муха, чтобы постепенно получить новые ответы в постоянное время за точку (постоянная относительно n = количество точек).

подробнее о чувствительные к местности хэши в целом или моя любимая версия, которая будет работать в этом случае.

детерминированный подход лучше, чем грубая сила

идея такова: для каждой точки поместите край круга на эту точку и проведите круг вокруг, чтобы увидеть, какой направление содержит наибольшее количество очков. Сделайте это для всех точек, и мы найдем global max.

развертка вокруг точки p может быть выполнена в N log n раз: (a) нахождение углового интервала в другой точке q таким образом, что когда мы помещаем круг под углом тета, то он содержит q; и (b) сортировка интервалов, чтобы мы могли маршировать/развертки вокруг p в линейное время.

таким образом, требуется O(N log n) время, чтобы найти лучший круг, касаясь фиксированной точки p, а затем умножить это на O (n) на выполните проверку для всех точек. Общее время O (N^2 log n).

если это правда, что точность не важна и алгоритм может делать небольшие ошибки, то я думаю следующее.

пусть f(x,y) - функция, которая имеет максимум в точке (0,0) и имеет значение только в точках внутри круга радиуса R. например, f(x,y) = e^{(x^2 + y^2)/ (2 * R^2)}.

пусть (x_i,y_i) и точки E_i(x,y) = f(x - x_i, y - y_i).

ваша проблема состоит в том, чтобы найти максимум \sum_i E_i(x,y) .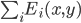

вы можете использовать градиентный спуск, начиная с каждого точка.

могу ли я предложить карту плотности? Найдите минимальную и максимальную границы для x и y. Разделите диапазон границ x и y на ячейки, имеющие ширину, равную диаметру вашего круга. Подсчитайте количество точек в каждой ячейке для x и y отдельно. Теперь найдите пересечение на карте плотности между самым высоким рангом X bin с самым высоким рангом y bin.

Это очень быстрый алгоритм для быстрого обобщения больших наборов данных, но он не всегда точен, чтобы улучшить точность вы можете нарезать бункеры на все меньшие и меньшие части или сдвинуть позиции бункера влево или вправо n раз и использовать систему голосования для выбора ответа, который чаще всего происходит между испытаниями.

вы можете пикселизировать всю область, затем перейти к каждой точке и увеличить значение всех пикселей в пределах круга радиуса вокруг этой точки. Пиксели с наибольшей суммой-хорошие кандидаты.

конечно, вы можете потерять некоторые хорошие области или" галлюцинировать " хорошие области из-за ошибок округления. Возможно, вы могли бы попробовать сначала сделать грубую пикселизацию, а затем уточнить перспективные области.

Это известный алгоритм k-ближайшей точки. Описано здесь:http://www.cs.ucsb.edu / ~suri / cs235 / ClosestPair.pdf