Аппроксимация обратных тригонометрических функций

в среде с фиксированной точкой (S15.16) я успешно использовал КОРДИЧЕСКИЙ алгоритм (см. Википедию для общего описания) для вычисления atan2(y,x), а затем получил asin () и acos () из этого, используя известные функциональные тождества, которые включают квадратный корень:

asin(x) = atan2 (x, sqrt ((1.0 + x) * (1.0 - x)))
acos(x) = atan2 (sqrt ((1.0 + x) * (1.0 - x)), x)

оказывается, найти полезное описание КОРДИЧЕСКОЙ итерации для atan2 () на двойнике сложнее, чем я думал. Следующий сайт содержит достаточно подробное описание, и также обсуждаются два альтернативных подхода, полиномиальная аппроксимация и таблицы поиска:

http://ch.mathworks.com/examples/matlab-fixed-point-designer/615-calculate-fixed-point-arctangent

вы можете использовать приближение: используйте бесконечные сериалы пока решение не будет достаточно близко для вас.

например:
arcsin(z) = Sigma((2n!)/((2^2n)*(n!)^2)*((z^(2n+1))/(2n+1))) где n в [0, бесконечность)

может быть, какая-то разумная грубая сила, как Ньютон рэпсон.

Итак, для решения asin () вы идете с крутым спуском на sin ()

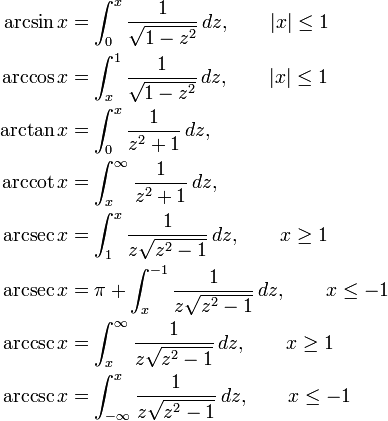
http://en.wikipedia.org/wiki/Inverse_trigonometric_functions#Expression_as_definite_integrals

вы можете сделать это интегрирование численно с помощью функции квадратного корня, аппроксимируя бесконечным рядом:

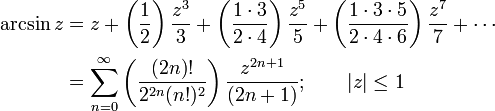
должно быть легко добавить следующий код в фиксированную точку. Он использует рациональное приближение для вычисления арктангенса, нормированного к интервалу [0 1) (Вы можете умножить его на Pi/2, чтобы получить реальный арктангенса). Затем, вы можете использовать известные личности чтобы получить arcsin / arccos из арктангенса.

normalized_atan(x) ~ (b x + x^2) / (1 + 2 b x + x^2)

where b = 0.596227

максимальная ошибка 0.1620 º

#include <stdint.h>
#include <math.h>

// Approximates atan(x) normalized to the [-1,1] range
// with a maximum error of 0.1620 degrees.

float norm_atan( float x )
{
    static const uint32_t sign_mask = 0x80000000;
    static const float b = 0.596227f;

    // Extract the sign bit
    uint32_t ux_s  = sign_mask & (uint32_t &)x;

    // Calculate the arctangent in the first quadrant
    float bx_a = ::fabs( b * x );
    float num = bx_a + x * x;
    float atan_1q = num / ( 1.f + bx_a + num );

    // Restore the sign bit
    uint32_t atan_2q = ux_s | (uint32_t &)atan_1q;
    return (float &)atan_2q;
}

// Approximates atan2(y, x) normalized to the [0,4) range
// with a maximum error of 0.1620 degrees

float norm_atan2( float y, float x )
{
    static const uint32_t sign_mask = 0x80000000;
    static const float b = 0.596227f;

    // Extract the sign bits
    uint32_t ux_s  = sign_mask & (uint32_t &)x;
    uint32_t uy_s  = sign_mask & (uint32_t &)y;

    // Determine the quadrant offset
    float q = (float)( ( ~ux_s & uy_s ) >> 29 | ux_s >> 30 ); 

    // Calculate the arctangent in the first quadrant
    float bxy_a = ::fabs( b * x * y );
    float num = bxy_a + y * y;
    float atan_1q =  num / ( x * x + bxy_a + num );

    // Translate it to the proper quadrant
    uint32_t uatan_2q = (ux_s ^ uy_s) | (uint32_t &)atan_1q;
    return q + (float &)uatan_2q;
} 

В случае, если вам нужно больше точности, есть 3-й порядок рационального функция:

normalized_atan(x) ~ ( c x + x^2 + x^3) / ( 1 + (c + 1) x + (c + 1) x^2 + x^3)

where c = (1 + sqrt(17)) / 8

который имеет максимальную ошибку приближения 0.00811 º

отправка здесь моего ответа из этого другой подобный вопрос.

nVidia имеет некоторые большие ресурсы, которые я использовал для собственного использования, несколько примеров:acos asin инструмент atan2 etc etc...

эти алгоритмы дают достаточно точные результаты. Вот прямой пример Python с их копией кода, вставленной в:

import math
def nVidia_acos(x):
    negate = float(x<0)
    x=abs(x)
    ret = -0.0187293
    ret = ret * x
    ret = ret + 0.0742610
    ret = ret * x
    ret = ret - 0.2121144
    ret = ret * x
    ret = ret + 1.5707288
    ret = ret * math.sqrt(1.0-x)
    ret = ret - 2 * negate * ret
    return negate * 3.14159265358979 + ret

и вот результаты для сравнения:

nVidia_acos(0.5)  result: 1.0471513828611643
math.acos(0.5)    result: 1.0471975511965976

Это довольно близко! Умножьте на 57.29577951, чтобы получить результаты в градусах, что также из их формулы "градусов".

используйте полиномиальное приближение. Наименьшие квадраты подходят проще всего (Microsoft Excel), а приближение Чебышева более точно.

этот вопрос был рассмотрен ранее:как работают тригонометрические функции?

только непрерывные функции аппроксимируются многочленами. И вычислить arcsin(X) является discontinous в точке x=1.тот же arccos (x).Но уменьшение диапазона до интервала 1, sqrt (1/2) в этом случае избежать этой ситуации. У нас есть arcsin(x)=pi/2 - arccos(x),arccos(x)=pi/2-arcsin (x).вы можете использовать matlab для минимаксного приближения.Апроксимировать только в диапазоне [0, sqrt(1/2)](если угол для этого arcsin больше, чем sqrt(1/2) найти cos(x).функция арктангенса только для x