Бесконечная поверхность конуса * испытание пересечения AABB

Я пытаюсь найти более быстрый алгоритм для проверки того, выровнена ли ось коническую поверхность пересекает объем ограничивающего прямоугольника, выровненного по оси.

текущий алгоритм, который я разработал, выглядит следующим образом:

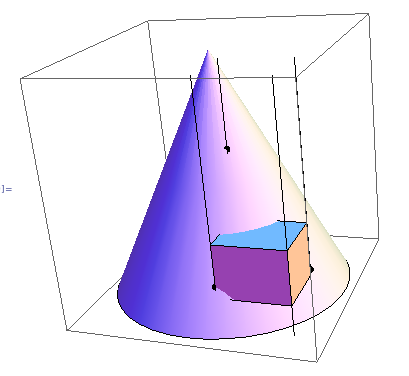
cone, AABB, lines along 4 parallel edges, and intersection points

  • x = 0
  • для каждого из любых 4 параллельных ребер AABB:
    • пересечь его линию с конусом.
    • если точка пересечения находится в пределах AABB:
      • возвращает true.
    • если точка пересечения находится на определенной стороне AABB:
      • x + = 1
  • если x == 0 или x == 4 (все пересечения были на одной стороне AABB):
    • возвращает false.
  • возвращает true.

может ли кто-нибудь придумать более эффективный? Это, кажется, делает много дополнительной работы, вычисляя каждое пересечение линий.

EDIT:

выше алгоритм плохой, например:

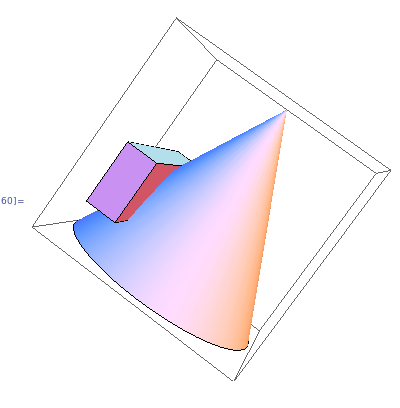
cone hits untested axis of box

конус может пересекать только один край коробки таким образом, что все пересечения осевой линии находятся на одной стороне, поэтому приведенный выше алгоритм не работает, если все ребра не проверены или ребра, которые будут проверены, разумно выбраны (возможно, ребра, ближайшие к конусу?).

EDIT EDIT: см. мой собственный ответ ниже для решения I позже обнаружен, что кажется мне почти оптимальным.

6
3d collision-detection geometry intersection

5 ответов

смотрим эта таблица тестов пересечения объекта/объекта похоже, что нет известного теста пересечения конуса/AABB. Так что, боюсь, вы сами по себе!

вы можете начать со статьи Дэвида Эберли"пересечение треугольника и конуса

2

Я нашел лучшее решение с помощью piman на #gamedev:

сделайте тест прямой окружности между верхней и нижней гранями AABB вдоль оси конуса с кругом, который конус делает на их плоскости.

Если оба прямоугольника находятся снаружи, AABB находится вне конуса.

2

Я нашел другое, возможно, оптимальное решение:

фон: уравнение для единичного отверстия правого конуса вдоль оси + - z равно x^2 + y^2-z^2 = 0

найдите максимум и минимум x^2 + y^2-z^2 над AABB. Подсказка: для x^2 минимальным является зажим(0, xmin, xmax)^2, а максимальным-max (xmin^2, xmax^2).

  • если результирующий интервал полностью отрицательный, коробка полностью находится внутри конуса.
  • если полученный интервал содержит 0, поле пересекает поверхность конуса.
  • если результирующий интервал полностью положительный, коробка полностью находится вне конуса.
2

на ссылка на статью Дэвида Эберли из @Gareth Rees хороший, но если вы разделите все на треугольники, вы в конечном итоге проверите избыточные вершины и ребра. Я думаю, что это будет работать так:

  1. (необязательно) проверьте, находится ли AABB полностью на противоположной стороне плоскости, перпендикулярной оси конуса. Если так, то перекрестка нет.

  2. проверьте каждую из 8 вершин, чтобы увидеть, находится ли она внутри конуса. При наличии таковых вершина есть, конус и AABB пересекаются. Это довольно прямолинейно, но это объясняется на странице 4 ссылки.

  3. проверьте каждый из 12 ребер, чтобы увидеть, пересекают ли они конус. Если какой-либо край делает, конус и AABB пересекаются. Это на стр. 4-5 ссылку.

  4. проверьте каждую из 6 граней, чтобы увидеть, пересекают ли они конус. Если какой-либо край делает, конус и AABB пересекаются. Достаточно к лучу проверки сформированному осью конуса против AABB; это довольно стандартный тест пересечения.

на самом деле может быть лучше поменять порядок проверки лица и края; я ожидал бы, что проверки лица будут быстрее, чем крайние, поэтому вы можете выйти раньше.

вероятно, есть некоторые хорошие возможности для оптимизации SIMD, так как количество вершин и ребер кратно 4, а конус выровнен по оси, но это выходит за рамки этого ответа :)

1

Я придумал алгоритм для решения общего случая произвольного конуса и aabb, но он по-прежнему эффективно обрабатывает ваш конкретный случай.

Я описал это в другом потоке: обнаружить, если куб и конус пересекаются друг с другом?

1