Библиотека Python curve fit, которая позволяет мне назначать границы параметрам

используйте преобразований переменных, как А2=Танха(А2'), А3=ехр(А3') или А5=А5^2.

как уже упоминалось Роб Фальк, вы можете использовать, например, процедуры нелинейной оптимизации scipy в scipy.минимизировать чтобы минимизировать произвольную функцию ошибки, например, среднюю квадратную ошибку.

обратите внимание, что функция, которую вы дали, не обязательно имеет реальные значения - возможно, именно поэтому ваша минимизация в pyminuit не сходилась. Вы должны относиться к этому немного более подробно, см. Пример 2.

примеры ниже оба используют L-BFGS-B метод минимизации, который поддерживает ограниченные области параметров. Я разделил этот ответ на две части:--8-->

1. функция с реальным codomain, напоминающий тот, который задан вами. Я добавил абсолютов для обеспечения функции вы дали возвращает реальные цифры в домене [-3,3)
2. фактическая функция, которую вы дали, которая имеет сложный кодомен

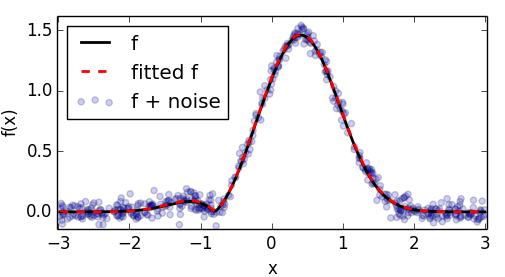
1. Настоящий кодомен

пример ниже показывает оптимизацию этого немного измененная версия вашей функции.

import numpy as np
import pylab as pl
from scipy.optimize import minimize

points = 500
xlim = 3.

def f(x,*p):
    a1,a2,a3,a4,a5 = p
    return a1*np.abs(x-a2)**a3 * np.exp(-a4 * np.abs(x)**a5)

# generate noisy data with known coefficients
p0 = [1.4,-.8,1.1,1.2,2.2]
x = (np.random.rand(points) * 2. - 1.) * xlim
x.sort()
y = f(x,*p0)
y_noise = y + np.random.randn(points) * .05

# mean squared error wrt. noisy data as a function of the parameters
err = lambda p: np.mean((f(x,*p)-y_noise)**2)

# bounded optimization using scipy.minimize
p_init = [1.,-1.,.5,.5,2.]
p_opt = minimize(
    err, # minimize wrt to the noisy data
    p_init, 
    bounds=[(None,None),(-1,1),(None,None),(0,None),(None,None)], # set the bounds
    method="L-BFGS-B" # this method supports bounds
).x

# plot everything
pl.scatter(x, y_noise, alpha=.2, label="f + noise")
pl.plot(x, y, c='#000000', lw=2., label="f")
pl.plot(x, f(x,*p_opt) ,'--', c='r', lw=2., label="fitted f")

pl.xlabel("x")
pl.ylabel("f(x)")
pl.legend(loc="best")
pl.xlim([-xlim*1.01,xlim*1.01])

pl.show()

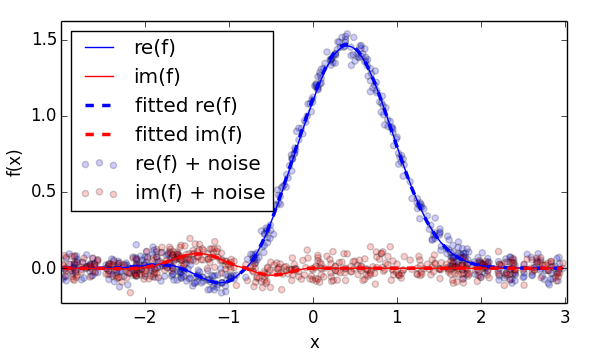
2. Расширение на сложный кодомен

расширение вышеуказанной минимизации до сложной области может быть сделано путем явного приведения к комплексным числам и адаптации функции ошибки:

во-первых, вы явно приведете значение x к комплексному значению, чтобы гарантировать, что f возвращает комплексные значения и может фактически вычислять дробные показатели отрицательных чисел. Во-вторых, мы вычисляем некоторую ошибку функция как на реальной, так и на мнимой частях - прямой кандидат является средним квадратом комплексных абсолютов.

import numpy as np
import pylab as pl
from scipy.optimize import minimize

points = 500
xlim = 3.

def f(x,*p):
    a1,a2,a3,a4,a5 = p
    x = x.astype(complex) # cast x explicitly to complex, to ensure complex valued f
    return a1*(x-a2)**a3 * np.exp(-a4 * x**a5)

# generate noisy data with known coefficients
p0 = [1.4,-.8,1.1,1.2,2.2]
x = (np.random.rand(points) * 2. - 1.) * xlim
x.sort()
y = f(x,*p0)
y_noise = y + np.random.randn(points) * .05 + np.random.randn(points) * 1j*.05

# error function chosen as mean of squared absolutes
err = lambda p: np.mean(np.abs(f(x,*p)-y_noise)**2)

# bounded optimization using scipy.minimize
p_init = [1.,-1.,.5,.5,2.]
p_opt = minimize(
    err, # minimize wrt to the noisy data
    p_init, 
    bounds=[(None,None),(-1,1),(None,None),(0,None),(None,None)], # set the bounds
    method="L-BFGS-B" # this method supports bounds
).x

# plot everything
pl.scatter(x, np.real(y_noise), c='b',alpha=.2, label="re(f) + noise")
pl.scatter(x, np.imag(y_noise), c='r',alpha=.2, label="im(f) + noise")

pl.plot(x, np.real(y), c='b', lw=1., label="re(f)")
pl.plot(x, np.imag(y), c='r', lw=1., label="im(f)")

pl.plot(x, np.real(f(x,*p_opt)) ,'--', c='b', lw=2.5, label="fitted re(f)")
pl.plot(x, np.imag(f(x,*p_opt)) ,'--', c='r', lw=2.5, label="fitted im(f)")

pl.xlabel("x")
pl.ylabel("f(x)")

pl.legend(loc="best")
pl.xlim([-xlim*1.01,xlim*1.01])

pl.show()

Примечания

кажется, минимизатор может быть немного чувствителен к начальным значениям - поэтому я разместил свою первую догадку (p_init) не слишком далеко от оптимального. Если вам нужно бороться с этим, вы можете использовать ту же процедуру минимизации в дополнение к глобальному циклу оптимизации, например тазик-скока или Брут.

вы могли бы использовать lmfit для таких проблем. Поэтому я добавляю пример (с другой функцией, чем вы используете, но она может легко адаптироваться) о том, как ее использовать, если кто-то заинтересован в этой теме.

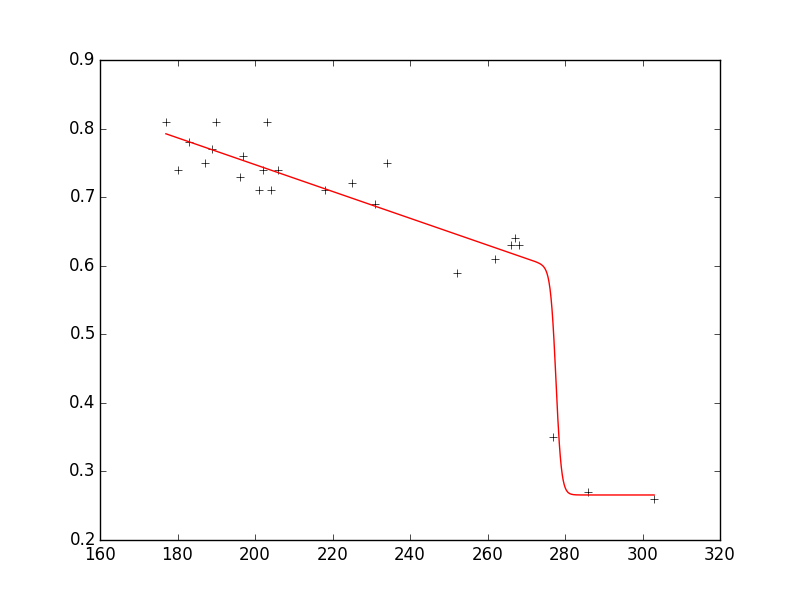
скажем, у вас есть набор данных следующим образом:

xdata = np.array([177.,180.,183.,187.,189.,190.,196.,197.,201.,202.,203.,204.,206.,218.,225.,231.,234.,
          252.,262.,266.,267.,268.,277.,286.,303.])

ydata = np.array([0.81,0.74,0.78,0.75,0.77,0.81,0.73,0.76,0.71,0.74,0.81,0.71,0.74,0.71,
      0.72,0.69,0.75,0.59,0.61,0.63,0.64,0.63,0.35,0.27,0.26])

и вы хотите, чтобы модель соответствовала данным, которые выглядят следующим образом:

model = n1 + (n2 * x + n3) * 1./ (1. + np.exp(n4 * (n5 - x)))

С ограничениями, которые

0.2 < n1 < 0.8
-0.3 < n2 < 0

используя lmfit (версия 0.8.3) вы затем получите следующий вывод:

n1:   0.26564921 +/- 0.024765 (9.32%) (init= 0.2)
n2:  -0.00195398 +/- 0.000311 (15.93%) (init=-0.005)
n3:   0.87261892 +/- 0.068601 (7.86%) (init= 1.0766)
n4:  -1.43507072 +/- 1.223086 (85.23%) (init=-0.36379)
n5:   277.684530 +/- 3.768676 (1.36%) (init= 274)

как вы можете видеть, fit воспроизводит данные очень хорошо, и параметры находятся в запрошенных диапазонах.

вот весь код, который воспроизводит сюжет с несколькими дополнительными комментариями:

from lmfit import minimize, Parameters, Parameter, report_fit
import numpy as np

xdata = np.array([177.,180.,183.,187.,189.,190.,196.,197.,201.,202.,203.,204.,206.,218.,225.,231.,234.,
      252.,262.,266.,267.,268.,277.,286.,303.])

ydata = np.array([0.81,0.74,0.78,0.75,0.77,0.81,0.73,0.76,0.71,0.74,0.81,0.71,0.74,0.71,
      0.72,0.69,0.75,0.59,0.61,0.63,0.64,0.63,0.35,0.27,0.26])

def fit_fc(params, x, data):

    n1 = params['n1'].value
    n2 = params['n2'].value
    n3 = params['n3'].value
    n4 = params['n4'].value
    n5 = params['n5'].value

    model = n1 + (n2 * x + n3) * 1./ (1. + np.exp(n4 * (n5 - x)))

    return model - data #that's what you want to minimize

# create a set of Parameters
# 'value' is the initial condition
# 'min' and 'max' define your boundaries
params = Parameters()
params.add('n1', value= 0.2, min=0.2, max=0.8)
params.add('n2', value= -0.005, min=-0.3, max=10**(-10))
params.add('n3', value= 1.0766, min=-1000., max=1000.)
params.add('n4', value= -0.36379, min=-1000., max=1000.)
params.add('n5', value= 274.0, min=0., max=1000.)

# do fit, here with leastsq model
result = minimize(fit_fc, params, args=(xdata, ydata))

# write error report
report_fit(params)

xplot = np.linspace(min(xdata), max(xdata), 1000)
yplot = result.values['n1'] + (result.values['n2'] * xplot + result.values['n3']) * \
                              1./ (1. + np.exp(result.values['n4'] * (result.values['n5'] - xplot)))
#plot results
try:
    import pylab
    pylab.plot(xdata, ydata, 'k+')
    pylab.plot(xplot, yplot, 'r')
    pylab.show()
except:
    pass

EDIT:

если вы используете версию 0.9.x вам нужно соответствующим образом настроить код; проверьте здесь какие изменения были внесены с 0.8.3 на 0.9.x.

библиотека Python (лицензия BSD), которая делает это:

https://github.com/zunzun/pyeq2

вы можете проверить его онлайн на http://zunzun.com

рассматривали ли вы его как задачу оптимизации и использование одной из процедур нелинейной оптимизации в scipy для минимизации ошибки наименьших квадратов путем изменения коэффициентов вашей функции? Многие процедуры в optimize допускают ограничения на независимые переменные.