Быстрый алгоритм b-сплайна с numpy/scipy
Мне нужно вычислить 3D bspline кривые в python. Я посмотрел на Сципиона.интерполировать.splprep и несколько других модулей scipy, но не смогли найти ничего, что легко дало бы мне то, что мне нужно. Поэтому я написал свой собственный модуль ниже. Код работает нормально, но он медленный (тестовая функция работает в 0.03 s, что кажется большим, учитывая, что я прошу только 100 образцов с 6 контрольными вершинами).
есть ли способ упростить код ниже с помощью нескольких вызовов модуля scipy, которые предположительно ускорить? А если нет, то что я могу сделать с моим кодом, чтобы улучшить его производительность?
import numpy as np
# cv = np.array of 3d control vertices
# n = number of samples (default: 100)
# d = curve degree (default: cubic)
# closed = is the curve closed (periodic) or open? (default: open)
def bspline(cv, n=100, d=3, closed=False):
# Create a range of u values
count = len(cv)
knots = None
u = None
if not closed:
u = np.arange(0,n,dtype='float')/(n-1) * (count-d)
knots = np.array([0]*d + range(count-d+1) + [count-d]*d,dtype='int')
else:
u = ((np.arange(0,n,dtype='float')/(n-1) * count) - (0.5 * (d-1))) % count # keep u=0 relative to 1st cv
knots = np.arange(0-d,count+d+d-1,dtype='int')
# Simple Cox - DeBoor recursion
def coxDeBoor(u, k, d):
# Test for end conditions
if (d == 0):
if (knots[k] <= u and u < knots[k+1]):
return 1
return 0
Den1 = knots[k+d] - knots[k]
Den2 = knots[k+d+1] - knots[k+1]
Eq1 = 0;
Eq2 = 0;
if Den1 > 0:
Eq1 = ((u-knots[k]) / Den1) * coxDeBoor(u,k,(d-1))
if Den2 > 0:
Eq2 = ((knots[k+d+1]-u) / Den2) * coxDeBoor(u,(k+1),(d-1))
return Eq1 + Eq2
# Sample the curve at each u value
samples = np.zeros((n,3))
for i in xrange(n):
if not closed:
if u[i] == count-d:
samples[i] = np.array(cv[-1])
else:
for k in xrange(count):
samples[i] += coxDeBoor(u[i],k,d) * cv[k]
else:
for k in xrange(count+d):
samples[i] += coxDeBoor(u[i],k,d) * cv[k%count]
return samples
if __name__ == "__main__":
import matplotlib.pyplot as plt
def test(closed):
cv = np.array([[ 50., 25., -0.],
[ 59., 12., -0.],
[ 50., 10., 0.],
[ 57., 2., 0.],
[ 40., 4., 0.],
[ 40., 14., -0.]])
p = bspline(cv,closed=closed)
x,y,z = p.T
cv = cv.T
plt.plot(cv[0],cv[1], 'o-', label='Control Points')
plt.plot(x,y,'k-',label='Curve')
plt.minorticks_on()
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(35, 70)
plt.ylim(0, 30)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
test(False)
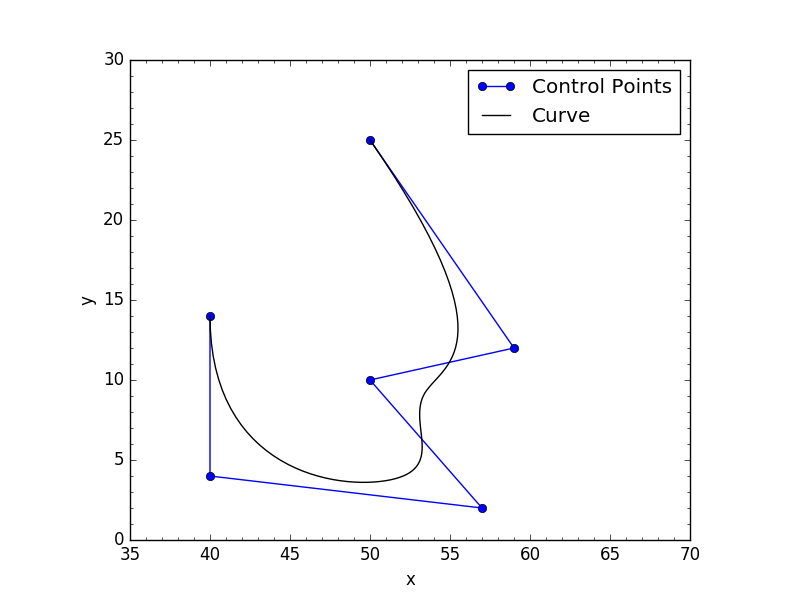
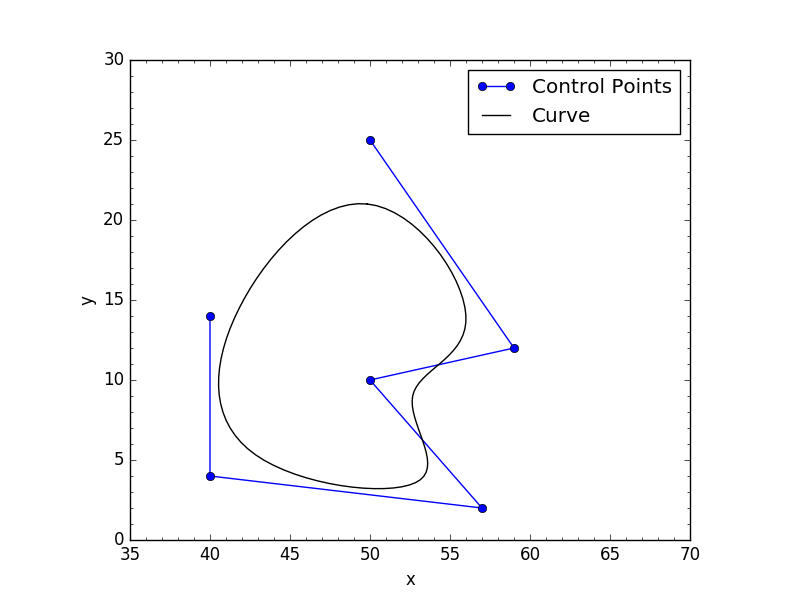
два изображения ниже показывают, что мой код возвращает с обоими закрытыми условиями:
2 ответов
Итак, после одержимости много о моем вопросе, и много исследований, я, наконец, мой ответ. Все доступно в scipy, и я помещаю свой код здесь, так что, надеюсь, кто-то еще может найти это полезным.
функция принимает массив из N-d точек, степень кривой, периодическое состояние (открытое или закрытое) и возвращает n образцов вдоль этой кривой. Есть способы убедиться, что образцы кривых равноудалены, но пока я сосредоточусь на этом вопросе, так как это все о скорости.
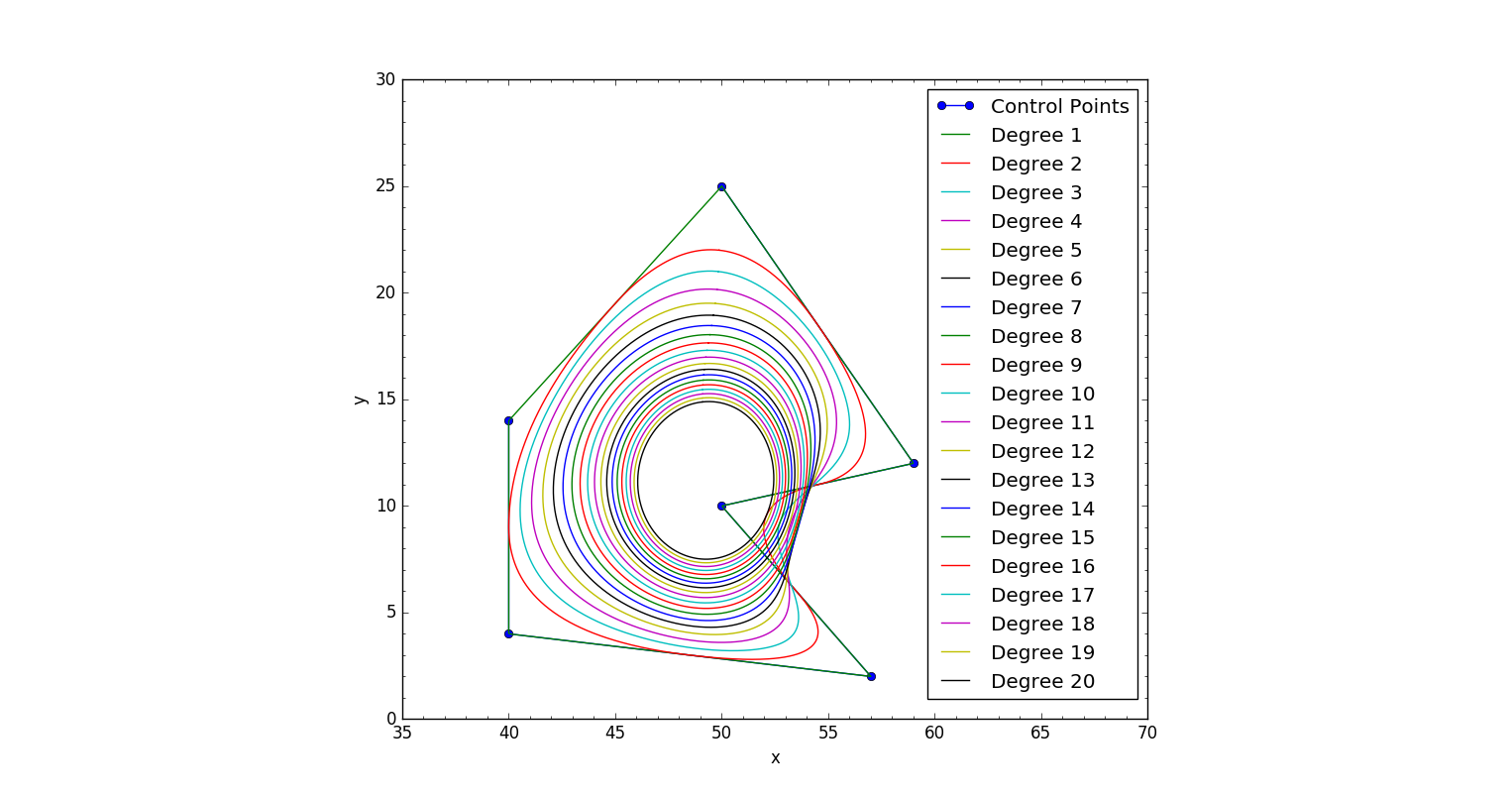
достойно внимания: я не могу, кажется, быть в состоянии выйти за кривую 20-й степени. Конечно, это уже перебор, но я подумал, что стоит упомянуть.
также стоит отметить: на моей машине код ниже может рассчитать 100 000 образцов в 0.017 s
import numpy as np
import scipy.interpolate as si
def bspline(cv, n=100, degree=3, periodic=False):
""" Calculate n samples on a bspline
cv : Array ov control vertices
n : Number of samples to return
degree: Curve degree
periodic: True - Curve is closed
False - Curve is open
"""
# If periodic, extend the point array by count+degree+1
cv = np.asarray(cv)
count = len(cv)
if periodic:
factor, fraction = divmod(count+degree+1, count)
cv = np.concatenate((cv,) * factor + (cv[:fraction],))
count = len(cv)
degree = np.clip(degree,1,degree)
# If opened, prevent degree from exceeding count-1
else:
degree = np.clip(degree,1,count-1)
# Calculate knot vector
kv = None
if periodic:
kv = np.arange(0-degree,count+degree+degree-1)
else:
kv = np.clip(np.arange(count+degree+1)-degree,0,count-degree)
# Calculate query range
u = np.linspace(periodic,(count-degree),n)
# Calculate result
return np.array(si.splev(u, (kv,cv.T,degree))).T
чтобы проверить это:
import matplotlib.pyplot as plt
colors = ('b', 'g', 'r', 'c', 'm', 'y', 'k')
cv = np.array([[ 50., 25.],
[ 59., 12.],
[ 50., 10.],
[ 57., 2.],
[ 40., 4.],
[ 40., 14.]])
plt.plot(cv[:,0],cv[:,1], 'o-', label='Control Points')
for d in range(1,21):
p = bspline(cv,n=100,degree=d,periodic=True)
x,y = p.T
plt.plot(x,y,'k-',label='Degree %s'%d,color=colors[d%len(colors)])
plt.minorticks_on()
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(35, 70)
plt.ylim(0, 30)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
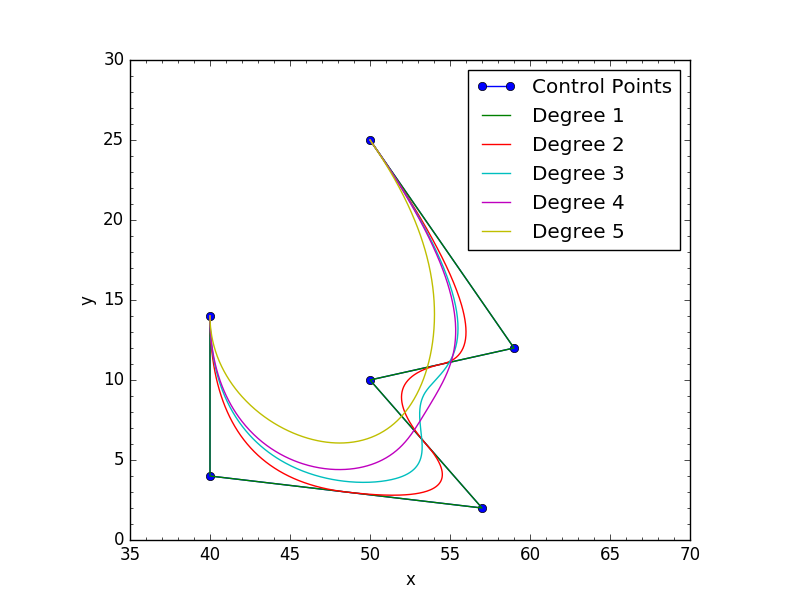
результаты как для открытых, так и для периодических кривые:
дополнительное соглашение
по состоянию на scipy-0.19.0 есть новый scipy.интерполировать.BSpline функция, которую можно использовать.
import numpy as np
import scipy.interpolate as si
def scipy_bspline(cv, n=100, degree=3, periodic=False):
""" Calculate n samples on a bspline
cv : Array ov control vertices
n : Number of samples to return
degree: Curve degree
periodic: True - Curve is closed
"""
cv = np.asarray(cv)
count = cv.shape[0]
# Closed curve
if periodic:
kv = np.arange(-degree,count+degree+1)
factor, fraction = divmod(count+degree+1, count)
cv = np.roll(np.concatenate((cv,) * factor + (cv[:fraction],)),-1,axis=0)
degree = np.clip(degree,1,degree)
# Opened curve
else:
degree = np.clip(degree,1,count-1)
kv = np.clip(np.arange(count+degree+1)-degree,0,count-degree)
# Return samples
max_param = count - (degree * (1-periodic))
spl = si.BSpline(kv, cv, degree)
return spl(np.linspace(0,max_param,n))
проверка на эквивалентность:
p1 = bspline(cv,n=10**6,degree=3,periodic=True) # 1 million samples: 0.0882 sec
p2 = scipy_bspline(cv,n=10**6,degree=3,periodic=True) # 1 million samples: 0.0789 sec
print np.allclose(p1,p2) # returns True
предоставление советов по оптимизации без профилирования данных немного похоже на съемку в темноте. Однако, функция coxDeBoor кажется, называется очень часто. Здесь я бы начал оптимизацию.
вызовы функций в Python дорогие. Вы должны попытаться заменить coxDeBoor рекурсия с итерацией, чтобы избежать чрезмерных вызовов функций. Некоторые общие сведения о том, как это сделать, можно найти в ответах на этот вопрос. В качестве стека/очереди вы можете использовать collections.deque.