C# / C++: как визуализировать многомерные массивы
например: двумерный массив можно визуализировать как кирпичную стену с квадратными кирпичами, где каждый кирпич представляет координату в нашем массиве. Трехмерный массив может быть визуализирован так же, как ящик или куб.
но, вот сложная часть, как вы визуализируете массив с несколькими (более 3) измерениями? Или, для этой части, как вы визуализируете массив не только с несколькими измерениями, но и с несколькими измерениями в нескольких слоях?
например: как вы визуализируете массив, такой как этот: массив[3,3,3,3][3,3][3,3,3,3,3][3]?
13 ответов
Как вы визуализируете массивы, действительно зависит от их практического использования. Если вы используете массивы для пространственных отношений, вы можете извлечь выгоду из представления его как Куба, но вы также теряете необходимость представлять более 3 измерений. Если вы действительно хотите реализовать четвертое измерение времени, вы можете просто представить себе, что ваш куб меняется с течением времени.
в противном случае вы можете отслеживать сильно связанных записей. Возможно, каждый из первых элементы-это галактика, элементы второго уровня-звездные скопления, элементы третьего уровня-солнечные системы, элементы четвертого уровня-планеты, элементы пятого уровня-континенты...
в этом случае вы можете представить, что это были массивы внутри массивов. Если вам нужен 4-мерный массив, вы можете представить себе куб, но каждый суб-куб на самом деле является одномерным массивом.
Если вам нужен 5-мерный массив, то вы можете представить себе куб, но каждый суб-куб разделен в вашем примере "кирпичной стены".
6-мерный куб с каждым суб-кубом, являющимся его собственным разделенным кубом.
Это имеет тенденцию разваливаться после 6 измерений. Помимо этого, обычно есть более практическая причина, по которой вам нужно так много измерений. Например, такие веб-сайты, как eHarmony, делают свое сопоставление, используя нормальную геометрию на 20+ -мерных пространствах. У вас есть одно измерение для "юмора", одно для "хорошей внешности", одно для "любви к магазинам"... Тогда вы можете взять два люди и применить формулу расстояния (квадрат каждого из размерных различий, добавить эти различия, квадратный корень) и определить, насколько совместимы два человека. Итак, если один человек забил "5, 3, 9, 2, 8, 4, 7, 3, 1" на нашей 9-мерной матрице личности и другой забил "9, 3, 7, 1, 8, 2, 8, 4, 7" тогда ваша совместимость:
sqrt((5-9)^2+(3-3)^2+(9-7)^2+...)
Это может быть применено к бесконечным измерениям и все еще работать. Поскольку эти измерения не применяются к пространству, однако, нет необходимости визуализируйте их такими. Вместо этого в данном конкретном случае мы можем представить его как одномерный массив с несколькими целочисленными значениями. Причина, по которой мы можем упростить этот массив, заключается в том, что наш многомерный массив содержит только один "1", а все остальные-"0"(что указывает на местоположение человека в этом массиве).
отходя от примера eHarmony, точка-после определенного количества измерений у вас обычно есть практическая цель для массив, который поддается методу его восприятия.
некоторые люди могут мысленно моделировать N-мерную геометрию для n > 3, по крайней мере, насколько просты формы, а некоторые не могут. (Я был очень удивлен, когда недавно разговаривал с кем-то, чья область была продвинутой N-мерной геометрией, чтобы узнать, что он не мог визуализировать гиперкуб, в то время как я могу найти его математику совершенно вне меня).
на самом деле это не обязательно. Действительно, это редко особенно необходимо для визуализации двумерного массива декартовой coördinates либо - когда вы используете 2-мерный массив на практике у вас есть какая-то цель для каждой оси, и эта цель становится более важной, чем любое визуальное представление.
Если вам нужно, то считайте, что 2-мерный массив также можно рассматривать как упорядоченный набор 1-мерных структур. Аналогично, 3-мерный массив можно рассматривать как упорядоченный набор 2-мерных структур или набор наборов 1-мерных (с этими наборами равного размера различные размеры перемещают вопросы в зубчатые массивы).
следовательно, 4-мерный массив можно считать упорядоченным набором 3-мерных структур и т. д.
ты не знаешь. Редко бывает, что вам нужно больше, чем 2 или 3 измерения. Если вам нужно больше, тогда, возможно, дополнительные измерения следует смоделировать как свойства объекта, в этом случае вы можете видеть их как атрибуты, а не пытаться представить какой-то мифический гиперкуб.
попробуйте быть subtractive об этом. Если вам нужно представить, скажем, десятимерный массив, то начните с представления множества всех n-мерных вещественных евклидовых векторных пространств для всех конечных неотрицательных целых чисел n. { R0, R1, R2, ... }
теперь представьте, что вы забираете почти все это, оставляя только R10.
теперь представьте, что вы убрали почти все это, так что у вас остались только целочисленные точки решетки в R10.
теперь представьте себе, забирая почти все , так что у вас просто гипер-прямоугольное подмножество целых точек решетки.
и вы закончили; это хорошая визуализация 10-мерного массива. Это действительно очень мало, когда вы думаете об этом как о подмножестве множества всех возможных n-мерных векторных пространств.
Если вас интересует тема многомерных пространств, вы можете прочитать мое нежное введение в некоторые интересные факты об алгоритмах поиска в многомерном векторном пространстве базы данных:
http://blogs.msdn.com/b/ericlippert/archive/tags/high+dimensional+spaces/
есть много прекрасных способов визуализации многомерных данных. Один из моих любимых-Альфред Инсельберг Параллельные Координаты, который представляет каждое измерение как вертикальную ось, и каждая точка данных как поток, соединяющий их все:
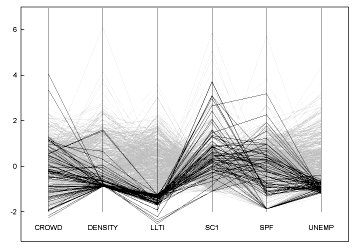
еще одна великая визуализация-Рамана РАО таблица объектив (pdf):
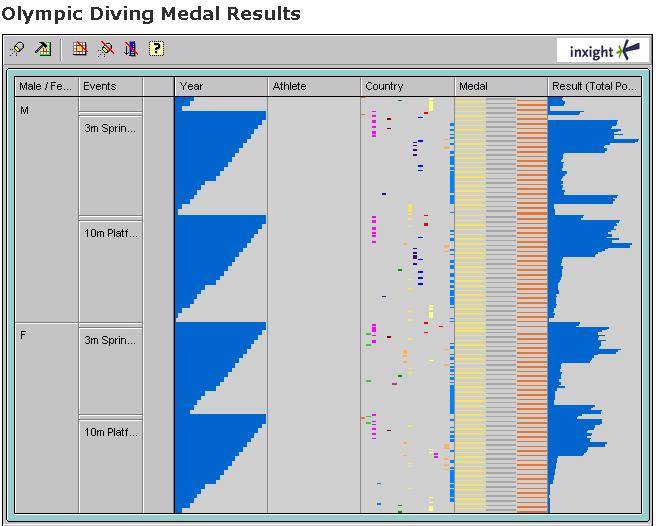
Это представляет каждое измерение в виде столбца, как в электронной таблице, но графически, а не численно. Он особенно хорошо показывает корреляцию между измерениями; когда вы сортируете по одному измерению, легко увидеть, как коррелированные измерения сортируются рядом с ним.
Так же, как вы визуализируете 4 пространственных измерения: "слайс", наложить, или на то, что вы уже понимаете и можете визуализировать.
подумайте о каждом дополнительном измерении как о "заключительной коробке". Подумайте о 2D-массиве как массиве 1D-массивов, о 3D-массиве как массиве 2D-массивов и т. д.
вот несколько примеров...
1D 1x2 массив:
[ 1, 2 ]
2D 2x2 массив:
{ [ 1, 2 ], [ 3, 4 ] }
{ [ 5, 6 ], [ 7, 8 ] }
массив 3D 2x2x2:
( { [ 1, 2 ], [ 3, 4 ] }, { [ 5, 6 ], [ 7, 8 ] } )
( { [ 9, 0 ], [ 1, 2 ] }, { [ 3, 4 ], [ 5, 6 ] } )
вы можете визуализировать финансовый отчет как массив, в котором данные поступают из нескольких объектов в виде электронной таблицы:
- одна электронная таблица данных о продажах будет 2D-массивом (например, продажи за каждый месяц в квартале на центр прибыли);
- несколько вкладок в книге (по одной для каждой дочерней компании) будут 3D-массивом;
затем, для целей глобальной консолидации, контроллер может получить книгу из каждого региона - это будет будьте 4-м измерением. Пятым измерением может быть "время", если вам нужно манипулировать данными о продажах с течением времени (например, для определения тенденций).
в теории, вы смогли держать многолетние, данные по продаж мульти-региона в одиночной переменной массива 5Д.
Как люди сказали выше, вам действительно нужно иметь приложение в виду, а затем логическая структура данных поможет определить подходящую физическую форму. Можно разместить любой набор атрибутов, которые можно моделировать relationally в массиве нормально.
Тони
визуализируйте массив 4D как массив 1D кубов. Массив 5D как 2D массив кубов. И 6D массив как 3D массив кубов, или куб кубов. Массив 7D как массив 1D кубов кубов и т. д...
игнорируя, являются ли эти размеры neeeded, почему бы просто не представить массив 4D как массив 1D (линия)"кубов". (т. е.: массив 1D, где каждый элемент указывает на 3D-куб). Это можно масштабировать по мере необходимости (т. е. 2D-поверхность, где каждый элемент указывает на куб). Это, конечно, не так, как гиперкуб будет "выглядеть", но это не требуется.
вкладки :)
вкладки трехмерных данных дают вам 4 измерения, вкладки вкладок дают вам N размерных.
не это обязательно лучший способ визуализировать его. Также не годится для вращения в любом из измерений.
но тогда, это зависит от того, что вы пытаетесь визуализировать
RGB, например, можно превратить в 2D-карту, а затем спроецировать на куб, давая вам информацию 4d
не глядя, чтобы отдать ферму здесь, но это пример того, как я смотрю на многомерные массивы в PHP.
$map[room][x][y][z][id][photopath][flag1][flag2]
Я представляю, как это будет выглядеть как точка в 3D-пространстве, затем я просто добавляю атрибуты сортировки. Вот, представьте, что вы играете Doom 3. Каждая карта делится на комнаты, которые имеют пиксели с координатами x, y и Z. Каждая из этих точек может иметь идентификатор объекта (monster, item и т. д.) связанный с ним. Я добавил больше атрибутов для своего приложения, но это в основном оно. Точка в массиве не обязательно должна быть геометрически точной; она может иметь любое значение. Похоже ли это на то, что делают другие люди, я не знаю. Я знаю, что использование графической библиотеки gd сделало бы хороший визуализатор для многомерных массивов на лету, но я не добрался до этого проекта в прошлый раз, когда работал на этого клиента.
