Численное решение ODE в Python
как численно решить оду в Python?
считают
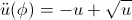
ddot{u}(phi) = -u + sqrt{u}
при следующих обстоятельствах
u(0) = 1.49907
и
dot{u}(0) = 0
С ограничением
0 <= phi <= 7pi.
затем, наконец, я хочу создать параметрический график, где координаты x и y генерируются как функция u.
проблема в том, что мне нужно запустить odeint дважды, так как это дифференциал второго порядка уравнение. Я попытался запустить его снова после первого раза, но он возвращается с ошибкой Якоби. Должен быть способ запустить его дважды одновременно.
здесь ошибка:
odepack.ошибка: функция и ее Якобиан должны быть вызываемыми функциями
который генерирует приведенный ниже код. Рассматриваемая строка-sol = odeint.
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from numpy import linspace
def f(u, t):
return -u + np.sqrt(u)
times = linspace(0.0001, 7 * np.pi, 1000)
y0 = 1.49907
yprime0 = 0
yvals = odeint(f, yprime0, times)
sol = odeint(yvals, y0, times)
x = 1 / sol * np.cos(times)
y = 1 / sol * np.sin(times)
plot(x,y)
plt.show()
редактировать
Я пытаюсь построить сюжет на стр. 9
вот сюжет с Mathematica
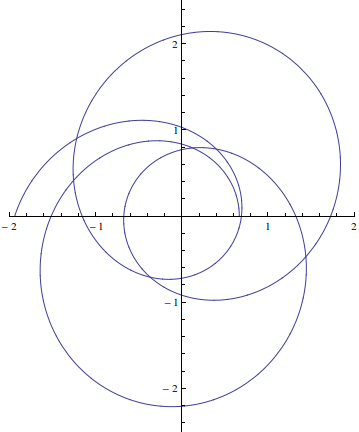
In[27]:= sol =
NDSolve[{y''[t] == -y[t] + Sqrt[y[t]], y[0] == 1/.66707928,
y'[0] == 0}, y, {t, 0, 10*[Pi]}];
In[28]:= ysol = y[t] /. sol[[1]];
In[30]:= ParametricPlot[{1/ysol*Cos[t], 1/ysol*Sin[t]}, {t, 0,
7 [Pi]}, PlotRange -> {{-2, 2}, {-2.5, 2.5}}]
4 ответов
import scipy.integrate as integrate
import matplotlib.pyplot as plt
import numpy as np
pi = np.pi
sqrt = np.sqrt
cos = np.cos
sin = np.sin
def deriv_z(z, phi):
u, udot = z
return [udot, -u + sqrt(u)]
phi = np.linspace(0, 7.0*pi, 2000)
zinit = [1.49907, 0]
z = integrate.odeint(deriv_z, zinit, phi)
u, udot = z.T
# plt.plot(phi, u)
fig, ax = plt.subplots()
ax.plot(1/u*cos(phi), 1/u*sin(phi))
ax.set_aspect('equal')
plt.grid(True)
plt.show()
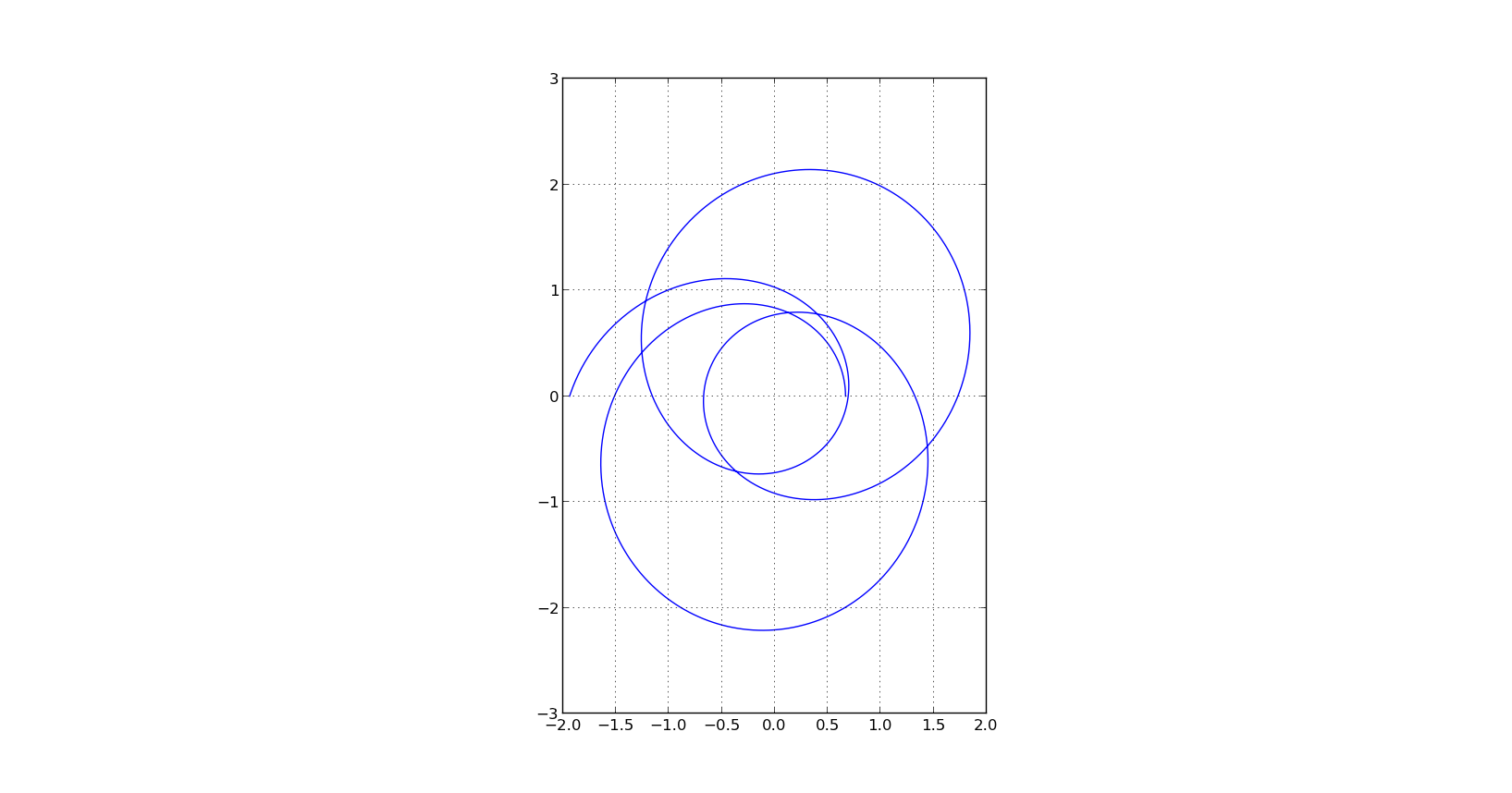
код от вашего другого вопрос это очень близко к тому, что вы хотите. Необходимы два изменения:
- вы решали другую оду (потому что вы изменили два знака внутри функции
deriv) - на
yкомпонент вашего желаемого участка исходит из значений решения, а не из значений первой производной решения, поэтому вам нужно заменитьu[:,0](значений функции) дляu[:, 1](дериваты.)
это конечный результат:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def deriv(u, t):
return np.array([u[1], -u[0] + np.sqrt(u[0])])
time = np.arange(0.01, 7 * np.pi, 0.0001)
uinit = np.array([1.49907, 0])
u = odeint(deriv, uinit, time)
x = 1 / u[:, 0] * np.cos(time)
y = 1 / u[:, 0] * np.sin(time)
plt.plot(x, y)
plt.show()
тем не менее, я предлагаю вам использовать код из ответа unutbu, потому что он сам документирует (u, udot = z) и использует np.linspace вместо np.arange. Затем запустите это, чтобы получить желаемую цифру:
x = 1 / u * np.cos(phi)
y = 1 / u * np.sin(phi)
plt.plot(x, y)
plt.show()
вы можете использовать scipy.интегрировать.ода. Чтобы решить dy / dt = f(t,y), с начальным условием y (t0)=y0, в момент времени=t1 с Рунге-Куттой 4-го порядка вы могли бы сделать что-то вроде этого:
from scipy.integrate import ode
solver = ode(f).set_integrator('dopri5')
solver.set_initial_value(y0, t0)
dt = 0.1
while t < t1:
y = solver.integrate(t+dt)
t += dt
Edit: вы должны получить производную в первом порядке, чтобы использовать численное интегрирование. Этого вы можете достичь, установив, например, z1=u и z2=du/dt, после чего у вас есть dz1/dt = z2 и dz2/dt = D^2u / dt^2. Замените их в исходное уравнение и просто повторите вектор dZ/ dt, который является первым порядок.
Edit 2: Вот пример кода для всего этого:
import numpy as np
import matplotlib.pyplot as plt
from numpy import sqrt, pi, sin, cos
from scipy.integrate import ode
# use z = [z1, z2] = [u, u']
# and then f = z' = [u', u''] = [z2, -z1+sqrt(z1)]
def f(phi, z):
return [z[1], -z[0]+sqrt(z[0])]
# initialize the 4th order Runge-Kutta solver
solver = ode(f).set_integrator('dopri5')
# initial value
z0 = [1.49907, 0.]
solver.set_initial_value(z0)
values = 1000
phi = np.linspace(0.0001, 7.*pi, values)
u = np.zeros(values)
for ii in range(values):
u[ii] = solver.integrate(phi[ii])[0] #z[0]=u
x = 1. / u * cos(phi)
y = 1. / u * sin(phi)
plt.figure()
plt.plot(x,y)
plt.grid()
plt.show()
