Что именно может вызвать подсчет до бесконечности в алгоритме Беллмана-Форда
из того, что я могу понять, подсчет до бесконечности происходит, когда один маршрутизатор подает другую старую информацию, которая продолжает распространяться по сети к бесконечности. Из того, что я читал, это определенно может произойти, когда ссылка удаляется.
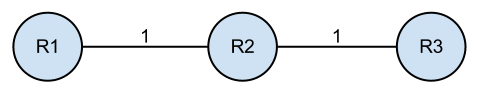
таким образом, в этом примере алгоритм Bellman-Ford будет сходиться для каждого маршрутизатора, у них будут записи друг для друга. R2 будет знать, что он может добраться до R3 по цене 1, а R1 будет знать, что он может добраться до R3 через R2 по цене 2.
Если связь между R2 и R3 отключена, то R2 будет знать, что он больше не может добраться до R3 по этой ссылке и удалит его из своей таблицы. Прежде чем он сможет отправить какие-либо обновления, возможно, он получит обновление от R1, которое будет рекламировать, что он может получить R3 по цене 2. R2 может добраться до R1 по цене 1, поэтому он обновит маршрут до R3 через R1 по цене 3. Затем R1 получит обновления от R2 позже и обновит свою стоимость до 4. Они затем будут продолжать кормить друг друга плохой информацией в бесконечность.
одна вещь, которую я видел, упоминал в нескольких местах, заключается в том, что могут быть другие причины подсчета до бесконечности, кроме просто ссылки в автономном режиме, такие как изменение стоимости ссылки. Я задумался об этом, и из того, что я могу сказать, мне кажется, что, возможно, стоимость увеличения связи может вызвать проблему. Однако я не вижу, что это возможно для снижения стоимости, чтобы вызвать проблема.
например, в приведенном выше примере, когда алгоритм сходится и R2 имеет маршрут к R3 по цене 1, а R1 имеет маршрут к R3 через R2 по цене 2. Если стоимость между R2 и R3 увеличивается до 5. Тогда это вызовет ту же проблему, R2 может получить обновление от R1, рекламирующее стоимость 2, и изменить ее стоимость на 3 через R1, R1, а затем изменить свой маршрут через R2 на стоимость 4 и так далее. Однако, если стоимость уменьшается на сходящемся маршруте, это не вызовет изменение. Правильно ли это? Это увеличение стоимости между связями, которые могут вызвать проблему, а не снижение стоимости? Есть ли другие возможные причины? Будет ли отключение маршрутизатора таким же, как и выход ссылки?
4 ответов
посмотрите на этот пример:
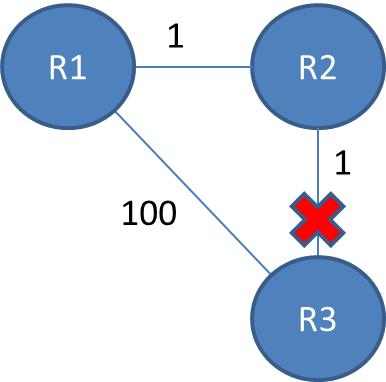
таблица маршрутизации будет:
R1 R2 R3
R1 0 1 2
R2 1 0 1
R3 2 1 0
теперь предположим, что соединение между R2 и R3 потеряно (вы можете сломать линию или средний маршрутизатор между ними упал).
после одной итерации отправки информации вы получите следующую таблицу маршрутизации:
R1 R2 R3
R1 0 1 2
R2 1 0 3
R3 2 3 0
это происходит потому, что R2, R3 больше не подключен, поэтому R2 "думает", что он может перенаправлять пакеты на R3 через R1, который имеет путь 2-так он получит путь веса 3.
после дополнительной итерации R1 "видит" R2 дороже, чем раньше, поэтому он изменяет свою таблицу маршрутизации:
R1 R2 R3
R1 0 1 4
R2 1 0 3
R3 4 3 0
и так далее, пока они не сойдутся на правильном значении - но это может занять много времени,особенно если (R1, R3) дорого.
это называется "считать до бесконечности" (если w(R1,R3)=infinity и это единственный путь, - он будет продолжать считать навсегда.)
обратите внимание, что когда стоимость между двумя маршрутизаторами повышается, вы столкнетесь с той же проблемой (предположим w(R2,R3) доходит до 50 в приведенном выше примере). То же самое произойдет - R2 постараюсь маршруту R3 via R1 без "осознания" это зависит от (R2,R3) а также, и вы получите те же первые шаги и сходятся, как только вы найдете правильную стоимость.
однако, если стоимость идет вниз - это не произойдет, так как новая стоимость лучше, чем текущий-и маршрутизатор R2 будет придерживаться той же маршрутизации с уменьшенной стоимостью и не будет пытаться проложить маршрут через R1.
согласно Википедии:
RIP использует разделенный горизонт с методом обратного отравления, чтобы уменьшить вероятность формирования петель и использует максимальное количество прыжков для противодействия проблеме "счет до бесконечности". Эти меры позволяют избежать образования циклов маршрутизации в некоторых, но не во всех случаях. Добавление времени удержания (отказ от обновления маршрута в течение нескольких минут после ретракции маршрута) позволяет избежать формирования цикла практически во всех случаях, но вызывает значительное увеличение время конвергенции.
в последнее время был разработан ряд протоколов вектора расстояния без петель-примечательными примерами являются EIGRP, DSDV и Babel. Они избегают образования цикла во всех случаях, но страдают от повышенной сложности, и их развертывание было замедлено успехом протоколов маршрутизации состояния связи, таких как OSPF.
http://en.wikipedia.org/wiki/Distance-vector_routing_protocol#Workarounds_and_solutions
Это не подтверждает часть алгоритма Беллмана-Форда вопроса, но это упрощенный ответ. Здесь идет.
обратите внимание на изображение оригинального плаката. Существует R1, R2 и R3; представляющие маршрутизаторы 1, 2 и 3 соответственно.
каждая ссылка стоит 1, и каждый переход стоит 1. Чтобы прыгать двумя маршрутизаторами (например: Р1 до Р3) rerquires стоимостью 2.
каждый маршрутизатор отслеживает затраты и обновляет информацию. Однако, если отсутствует значение (например, недостающее звено между маршрутизаторами), счетчик переходов удаляется и заполняется другим маршрутизатором при обновлении таблиц маршрутизации.
пример:
Если связь маршрутизатора 3 с маршрутизатором 2 идет вниз, маршрутизатор 2 удалит маршрут из его таблицы. Маршрутизатор 1 по-прежнему считает, что требуется два прыжка, чтобы добраться до маршрутизатора 3. Это реплицируется на маршрутизатор 2, и теперь оба маршрутизатора думают, что требуется два прыжка, чтобы добраться до маршрутизатора 3.
маршрутизатор 1 делает простую математику, " Если это мне нужно один прыжок, чтобы добраться до маршрутизатора 2, и маршрутизатор 2 занимает два прыжка, чтобы добраться до маршрутизатора 3, мне нужно три прыжка, чтобы добраться до маршрутизатора 3. Блестяще!"Маршрутизатор 2 делает аналогичную математику и добавляет один прыжок к его маршруту и так далее.
вот как работает цикл.
Hold downs:
- по мере увеличения метрики задержка распространения информации
ограничения:
- задержки сходимости петли избегания
- полная информация о пути в рекламе маршрута
- явные запросы для циклов (например, двойной) Split horizon
- никогда не рекламируйте пункт назначения через его следующий прыжок
- A не рекламирует C до B
- яд обратного: Отправить отрицательную информацию при рекламе назначения через его следующий прыжок
- a рекламирует C до B с метрикой ∞
- ограничение: работает только для "петли" s размера 2
