Что означает O(log n)?

многие хорошие ответы уже были опубликованы на этот вопрос, но я считаю, что мы действительно упускаем важный - а именно, иллюстрированный ответ.

что значит сказать, что высота полного двоичного дерева равна O (log n)?

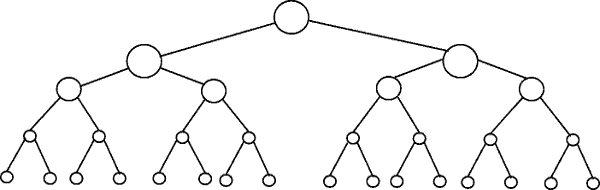
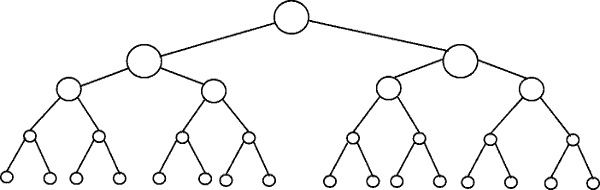
на следующем рисунке изображено двоичное дерево. Обратите внимание, что каждый уровень содержит двойное количество узлов по сравнению с уровнем выше (следовательно бинарные):

бинарный поиск является примером сложности O(log n). Допустим, узлы нижнего уровня дерева на рис. 1 представляют элементы некоторой отсортированной коллекции. Бинарный поиск-это алгоритм "разделяй и властвуй", и на рисунке показано, как нам понадобится (самое большее) 4 сравнения, чтобы найти запись, которую мы ищем в этом наборе данных из 16 элементов.

предположим, что вместо этого у нас был набор данных с 32 элементы. Продолжайте рисовать выше, чтобы найти, что теперь нам понадобится 5 сравнений, чтобы найти то, что мы ищем, так как дерево стало только на один уровень глубже, когда мы умножили количество данных. В результате сложность алгоритма можно описать как логарифмический порядок.

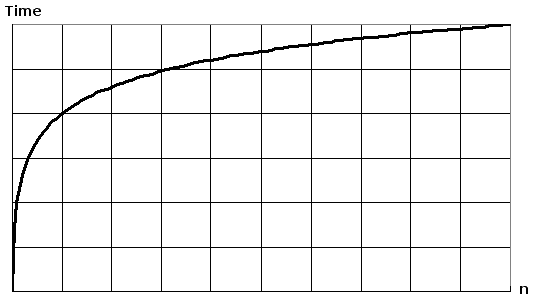
заговор log(n) на простом листе бумаги, приведет к графу, где подъем кривой замедляется как n увеличивается:

O(log N) в основном означает, что время идет линейно, в то время как n растет экспоненциально. Так что если это займет 1 во-вторых, чтобы вычислить 10 элементы, потребуется 2 секунды, чтобы вычислить 100 элементов 3 секунд для вычисления 1000 элементов, и так далее.

это O(log n) когда мы разделяем и покоряем тип алгоритмов e.G двоичный поиск. Другой пример-быстрая сортировка, где каждый раз мы делим массив на две части и каждый раз, когда он берет O(N) время, чтобы найти элемент pivot. Отсюда N O(log N)

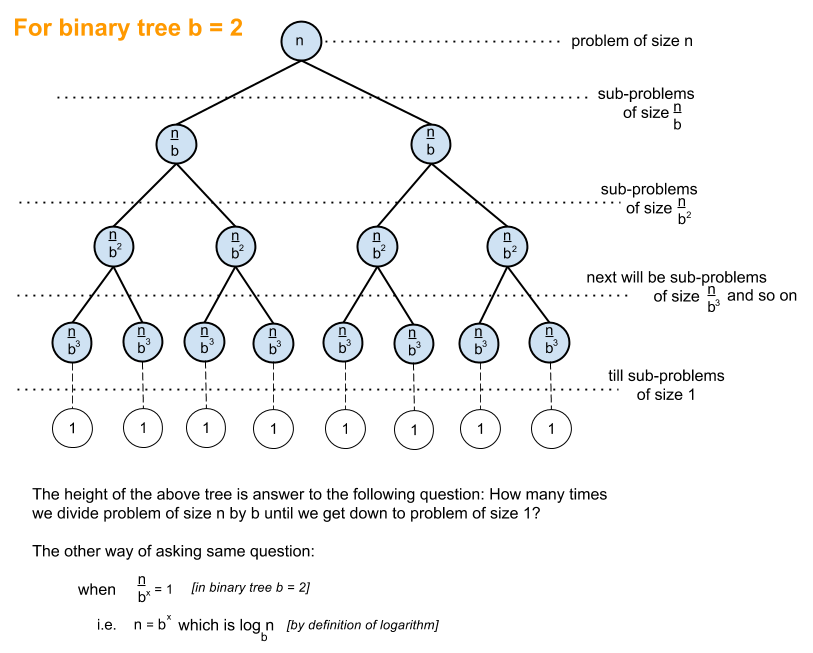
приведенное ниже объяснение использует случай полностью сбалансированной бинарное дерево, чтобы помочь вам понять, как мы получим логарифмическую сложность.

двоичное дерево-это случай, когда задача размера n делится на подзадачу размера n / 2, пока мы не достигнем задачи размера 1:

и вот как вы получаете O (log n), который представляет собой объем работы, которую необходимо выполнить на вышеуказанном дереве для достижения решения.

общим алгоритмом с O(log n) временной сложностью является двоичный поиск, рекурсивное отношение которого равно T(n/2) + O (1), т. е. на каждом последующем уровне дерева вы делите задачу на половину и выполняете постоянный объем дополнительной работы.

Если у вас есть функция, которая принимает:

1 millisecond to complete if you have 2 elements.
2 milliseconds to complete if you have 4 elements.
3 milliseconds to complete if you have 8 elements.
4 milliseconds to complete if you have 16 elements.
...
n milliseconds to complete if you have 2**n elements.

тогда требуется log₂(n) время. The Big O notation, грубо говоря, означает, что отношение должно быть истинным только для большого n, и что постоянные факторы и меньшие члены можно игнорировать.

обзор

другие дали хорошие примеры диаграмм, таких как диаграммы дерева. Я не видел простых примеров кода. Поэтому в дополнение к моему объяснению я предоставлю некоторые алгоритмы с простыми операторами печати, чтобы проиллюстрировать сложность различных категорий алгоритмов.

во-первых, вы захотите иметь общее представление о Логарифме, которое вы можете получить от https://en.wikipedia.org/wiki/Logarithm . Естественная наука использовать e и натуральный логарифм. Инженерные ученики будут использовать log_10 (log base 10), а компьютерные ученые будут использовать log_2 (log base 2) много, так как компьютеры основаны на двоичном коде. Иногда вы увидите сокращения естественного журнала как ln() инженеры обычно оставляют _10 и просто использовать log() и log_2 сокращается как lg(). Все типы логарифмов растут аналогичным образом, поэтому они разделяют одну и ту же категорию log(n).

когда вы смотрите на примеры кода ниже, я рекомендую посмотреть на O(1), затем O(n), затем O (n^2). После того, как вы хорошо с ними справитесь, посмотрите на остальных. Я включил чистые примеры, а также вариации, чтобы продемонстрировать, как тонкие изменения могут привести к той же классификации.

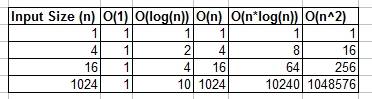
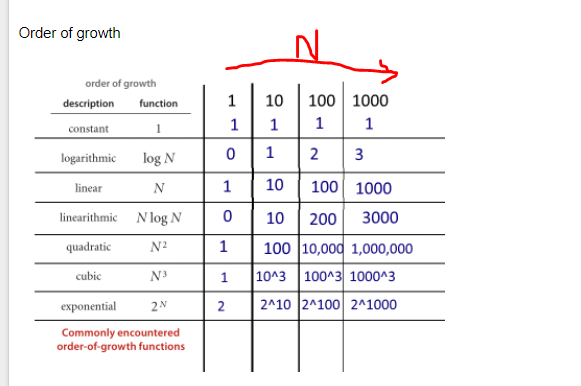
вы можете думать о O(1), O(n), O (logn) и т. д. как о классах или категориях роста. Для некоторых категорий потребуется больше времени, чем для других. Эти категории помогают нам упорядочить производительность алгоритма. Некоторые выросли быстрее, так как вход n растет. В нижеследующей таблице этот рост показан численно. В приведенной ниже таблице подумайте о log (n) как о потолке log_2.

Простые Примеры Кода Различных Категорий Big O:

O (1) - Примеры Постоянного Времени:

• 1:

алгоритм 1 печатает hello один раз, и это не зависит от n, поэтому он всегда будет работать в постоянное время, так что это O(1).

print "hello";

• 2:

алгоритм 2 печатает привет 3 раза, однако он не зависит от размера ввода. Даже когда n растет, этот алгоритм всегда будет печатать hello только 3 раза. Это, как говорится, 3, является константой, поэтому этот алгоритм также O(1).

print "hello";
print "hello";
print "hello";

O (log (n)) - логарифмический Примеры:

• алгоритм 3 - это действует как "log_2"

алгоритм 3 демонстрирует алгоритм, который работает в log_2 (n). Обратите внимание, что операция post цикла for кратна текущему значению i на 2, поэтому i идет от 1 до 2 до 4 до 8 до 16 до 32 ...

for(int i = 1; i <= n; i = i * 2)
  print "hello";

• алгоритм 4-это действует как "log_3"

алгоритм 4 демонстрирует log_3. Уведомление i идет от 1 до 3 до 9 до 27...

for(int i = 1; i <= n; i = i * 3)
  print "hello";

• алгоритм 5-это действует как " log_1.02"

алгоритм 5 важен, так как он помогает показать, что до тех пор, пока число больше 1 и результат многократно умножается против самого себя, вы смотрите на логарифмический алгоритм.

for(double i = 1; i < n; i = i * 1.02)
  print "hello";

O (n) - примеры Линейного Времени:

• 6

этот алгоритм прост, который печатает hello n раз.

for(int i = 0; i < n; i++)
  print "hello";

• 7

этот алгоритм показывает вариант, где он будет печатать hello n / 2 раза. n / 2 = 1/2 * n. Мы игнорируем константу 1/2 и видим, что этот алгоритм равен O(n).

for(int i = 0; i < n; i = i + 2)
  print "hello";

O(n*log(n)) - NLog (n) примеры:

• 8

подумайте об этом как о комбинации O(log(n)) и O(n). Вложенность циклов for помогает нам получить O(n*log(n))

for(int i = 0; i < n; i++)
  for(int j = 1; j < n; j = j * 2)
    print "hello";

• алгоритм 9

алгоритм 9 похож на алгоритм 8, но каждый из циклов допускает вариации, которые по-прежнему приводят к конечному результату O(n*log(n))

for(int i = 0; i < n; i = i + 2)
  for(int j = 1; j < n; j = j * 3)
    print "hello";

O (n^2) - N в квадрате Примеры:

• алгоритм 10

O(n^2) легко получается путем вложения стандарта для петель.

for(int i = 0; i < n; i++)
  for(int j = 0; j < n; j++)
    print "hello";

• алгоритм 11

как алгоритм 10, но с некоторыми вариациями.

for(int i = 0; i < n; i++)
  for(int j = 0; j < n; j = j + 2)
    print "hello";

O (n^3) - N кубических примеров:

• алгоритм 12

это как алгоритм 10, но с 3 петлями вместо 2.

for(int i = 0; i < n; i++)
  for(int j = 0; j < n; j++)
    for(int k = 0; k < n; k++)
      print "hello";

• 13

как алгоритм 12, но с некоторыми вариациями, которые все еще дают O(n^3).

for(int i = 0; i < n; i++)
  for(int j = 0; j < n + 5; j = j + 2)
    for(int k = 0; k < n; k = k + 3)
      print "hello";

резюме

выше приведено несколько прямых примеров и вариаций, чтобы продемонстрировать, какие тонкие изменения могут быть введены, которые действительно не изменяют анализ. Надеюсь, это даст вам достаточно понимания.

логарифмическое время (O(log n)) по существу означает, что время выполнения возрастает пропорционально логарифм размера входного сигнала-как пример, Если 10 деталей принимают самое большее некоторое количество времени x, и 100 пунктов занимает не более, скажем,2x, и 10 000 деталей принимают самое большее 4x, тогда это выглядит как O(log n) сложность времени.

логарифм

Ок давай попробуем и полностью понять, что такое логарифм на самом деле.

Теперь, если веревка зациклена один раз, лошади нужно будет тянуть в 10 раз сильнее. Если человек решит усложнить задачу лошади, он может снова обмотать веревку вокруг шеста, увеличив ее прочность еще в 10 раз. Третья петля снова увеличит силу еще в 10 раз.

мы видим, что для каждого цикла, значение увеличивается на 10. Количество оборотов, необходимых для получения любого числа, называется логарифмом числа, т. е. нам нужно 3 сообщения, чтобы умножить вашу силу в 1000 раз, 6 сообщений, чтобы умножить вашу силу на 1,000,000.

3-логарифм 1000, а 6-логарифм 1 000 000 (основание 10).

так что же на самом деле означает O(log n)?

В нашем примере выше, рост наш составляет O (log n). Для каждой дополнительной петли, сила наша веревочка может отрегулировать 10 раз больше:

Turns | Max Force
  0   |   1
  1   |   10
  2   |   100
  3   |   1000
  4   |   10000
  n   |   10^n

Теперь пример выше использовал базу 10, но, к счастью, база журнала незначительна, когда мы говорим о большой o нотации.

Теперь представим, что вы пытаетесь угадать число между 1-100.

Your Friend: Guess my number between 1-100! 
Your Guess: 50
Your Friend: Lower!
Your Guess: 25
Your Friend: Lower!
Your Guess: 13
Your Friend: Higher!
Your Guess: 19
Your Friend: Higher!
Your Friend: 22
Your Guess: Lower!
Your Guess: 20
Your Friend: Higher!
Your Guess: 21
Your Friend: YOU GOT IT!  

Теперь вам понадобилось 7 попыток, чтобы получить это право. Но что такое отношения здесь? Каково наибольшее количество предметов, которые вы можете угадать из каждой дополнительной догадки?

Guesses | Items
  1     |   2
  2     |   4
  3     |   8
  4     |   16
  5     |   32
  6     |   64
  7     |   128
  10    |   1024

используя график, мы можем видеть, что если мы используем двоичный поиск, чтобы угадать число между 1-100, это займет у нас максимум 7 попыток. Если бы у нас было 128 чисел, мы также могли бы угадать число в 7 попытках, но 129 чисел будет принимать нас максимум 8 попыток (в отношении логарифмов, здесь нам понадобится 7 догадок для диапазона значений 128, 10 догадок для Диапазон значений 1024. 7-логарифм 128, 10-логарифм 1024 (основание 2)).

обратите внимание, что я выделил жирным шрифтом "не более". Большая буква " О " всегда относится к худшему случаю. Если Вам повезет, вы можете угадать число с одной попытки, и поэтому лучший случай-O (1), но это другая история.

мы видим, что для каждого угадать наш набор данных сокращается. Хорошее эмпирическое правило, чтобы определить, если алгоритм имеет время logarithmtic это чтобы увидеть, сжимается ли набор данных по определенному порядку после каждой итерации

как насчет O (N log n)?

вы в конечном итоге столкнетесь с linerarithmic времени O (N log (n). Эмпирическое правило выше применяется снова, но на этот раз логарифмическая функция должна выполняться n раз, например, уменьшение размера списка N раз, что происходит в алгоритмах, таких как mergesort.

вы можете легко определить, является ли алгоритмическое Время N log n. Смотри для внешнего цикла, который повторяет список (O (n)). Затем посмотрите, есть ли внутренняя петля. Если внутренний цикл сокращение/сокращение набор данных на каждой итерации, этот цикл (O (log n), и поэтому общий алгоритм = O (N log n).

отказ от ответственности: пример веревки-логарифма был схвачен из отличного восторженная книга математика У. Сойера.

вы можете думать о O(log N) интуитивно, говоря, что время пропорционально количеству цифр в N.

Если операция выполняет постоянную временную работу над каждой цифрой или битом входного сигнала, вся операция займет время, пропорциональное количеству цифр или битов во входном сигнале, а не величине входного сигнала; таким образом, O(log N), а не O(N).

Если операция принимает ряд решений постоянного времени, каждое из которых наполовину (уменьшается в 3, 4, 5 раза..) размер входного сигнала, котор нужно рассматривать, все примет время пропорциональное к основанию журнала 2 (основанию 3, основанию 4, основанию 5...) размера n входного сигнала, а не O(N).

и так далее.

лучший способ, которым мне всегда приходилось мысленно визуализировать алгоритм, который работает в O (log n), заключается в следующем:

Если вы увеличиваете размер задачи на мультипликативную величину (т. е. умножаете ее размер на 10), работа увеличивается только на аддитивную величину.

применяя это к вашему вопросу двоичного дерева, у вас есть хорошее приложение: если вы удваиваете количество узлов в двоичном дереве, высота увеличивается только на 1 (аддитивная сумма). Если вы удвоите его снова, это по-прежнему увеличивается только на 1. (Очевидно, я предполагаю, что он остается сбалансированным и таким). Таким образом, вместо того, чтобы удвоить свою работу, когда размер проблемы умножается, вы делаете только немного больше работы. Вот почему алгоритмы O (log n) потрясающие.

что такое log_b(n)?

это количество раз, когда вы можете вырезать журнал длины n повторно на B равных частей, прежде чем достичь раздела размера 1.

сначала я рекомендую вам прочитать следующие книги;

алгоритмов (4-е издание)

вот некоторые функции и их сложности. Цифры указывают частоты выполнения оператора.

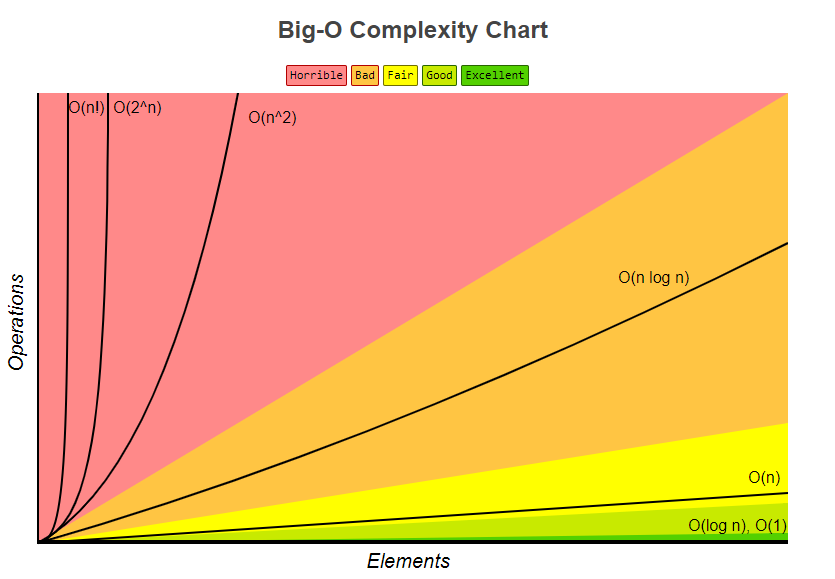
после Диаграмма Сложности Big-O и bigocheatsheet

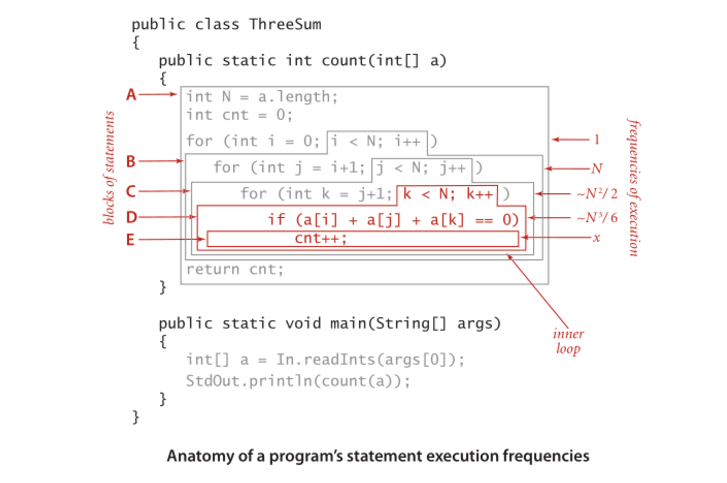
наконец, очень простая витрина есть показывает, как он рассчитывается;

Анатомия частот выполнения оператора программы.

анализ времени работы программы (пример).

алгоритмы разделения и завоевания обычно имеют logn компонент времени выполнения. Это происходит из-за многократного сокращения наполовину входных данных.

в случае двоичного поиска каждая итерация выбрасывает половину входных данных. Следует отметить, что в нотации Big-O log является базой журнала 2.

Edit: как уже отмечалось, база журналов не имеет значения, но при получении производительности Big-O алгоритма коэффициент журнала будет поступать из половины, поэтому я думаю об этом как о базе 2.

но что такое O(log n)? Например, что значит сказать, что высота двоичного дерева a >complete равна O(log n)?

Я бы перефразировал это как "высота полного двоичного дерева-log n". Вычисление высоты полного двоичного дерева будет O (log n), если вы шаг за шагом спускаетесь вниз.

Я не могу понять, как определить функции с логарифмической время.

логарифма по существу, обратная экспоненциальность. Итак, если каждый " шаг " вашей функции устраняет фактор элементов из исходного набора элементов, то есть логарифмического алгоритма времени.

для примера дерева вы можете легко увидеть, что шаг вниз по уровню узлов сокращает экспоненциальное число элементов по мере продолжения обхода. Популярный пример просмотра телефонной книги, отсортированной по имени, по существу эквивалентен переходу вниз по дереву двоичного поиска (средняя страница является корневым элементом, и вы можете вывести на каждом шаге, нужно ли идти влево или вправо).

O(log n) относится к функции (или алгоритму, или шагу в алгоритме), работающей в течение времени, пропорционального логарифму (обычно база 2 в большинстве случаев, но не всегда, и в любом случае это несущественно по нотации big-O*) размера входного сигнала.

логарифмическая функция является обратной экспоненциальной функции. Другими словами, если ваш вход растет экспоненциально (а не линейно, как вы обычно считаете), ваша функция растет линейно.

O(log n) времена выполнения очень распространены в любом виде приложения "разделяй и властвуй", потому что вы (в идеале) каждый раз сокращаете работу пополам. Если на каждом из этапов деления или завоевания вы выполняете постоянную временную работу (или работу, которая не является постоянной-время, но со временем растет медленнее, чем O(log n)), то вся ваша функция O(log n). Довольно часто для каждого шага требуется линейное время на входе; это составит общее время сложность O(n log n).

сложность двоичного поиска во время работы является примером O(log n). Это потому, что в двоичном поиске вы всегда игнорируете половину своего ввода на каждом последующем шаге, разделяя массив пополам и фокусируясь только на одной половине с каждым шагом. Каждый шаг является постоянным, потому что в двоичном поиске вам нужно сравнить только один элемент с вашим ключом, чтобы выяснить, что делать дальше, независимо от того, насколько большой массив вы рассматриваете в любой момент. Таким образом, Вы делаете приблизительно шаги log(n)/log(2).

сложность времени выполнения сортировки слиянием является примером O(n log n). Это происходит потому, что вы делите массив пополам с каждым шагом, в результате чего в общей сложности примерно log(n)/log(2) шаги. Однако на каждом шаге вам нужно выполнить операции слияния для всех элементов (будь то одна операция слияния для двух подложек из n / 2 элементов или две операции слияния для четырех подложек из n / 4 элементов), не имеет значения, поскольку это добавляет к сделать это для n элементов на каждом шаге). Таким образом, общая сложность O(n log n).

*помните, что обозначение big-O,по определению константы не имеет значения. Также изменение базы правил для логарифмов единственное различие между логарифмами различных оснований является постоянным фактором.

проще говоря: на каждом шаге алгоритма вы можете сократить работу наполовину. (Асимптотически эквивалентно третьему, четвертому, ...)

Это просто означает, что время, необходимое для этой задачи, растет с log(n) (пример : 2s для n = 10, 4s для n = 100,...). Читайте статьи Википедии на Алгоритм Бинарного Поиска и Big O Notation дополнительные уточнения.

Если вы построите логарифмическую функцию на графическом калькуляторе или что-то подобное, вы увидите, что она поднимается очень медленно-даже медленнее, чем линейная функция.

вот почему алгоритмы с логарифмической временной сложностью очень востребованы: даже для действительно большого n (скажем, n = 10^8, например) они работают более чем приемлемо.

эти 2 случая займут O (log n) время

case 1: f(int n) {
      int i;
      for (i = 1; i < n; i=i*2)
        printf("%d", i);
    }


 case 2  : f(int n) {
      int i;
      for (i = n; i>=1 ; i=i/2)
        printf("%d", i);
    }

O (log n) немного вводит в заблуждение, точнее это O(log₂ n), т. е. (логарифм с основанием 2).

высота сбалансированного двоичного дерева равна O (log₂ n), так как каждый узел имеет два (обратите внимание на "два", как в log₂ n) дочерние узлы. Итак, дерево с n узлами имеет высоту log₂ n.

Другим примером является двоичный поиск, который имеет время работы O (log₂ n) потому что на каждом шаге вы разделяете поиск пространства 2.

но что такое O (log n)

что это означает именно " как n стремится к infinity на time стремится к a*log(n) здесь a - постоянный коэффициент масштабирования".

или на самом деле это не совсем так; скорее это означает что-то вроде "time разделить на a*log(n) стремится к 1".

"стремится к" имеет обычное математическое значение из "анализа": например, что " если вы выбираете любой произвольно малая ненулевая постоянная k, то я могу найти соответствующее значение X такое, что ((time/(a*log(n))) - 1) меньше k для всех значений n больше X."

в терминах lay это означает, что уравнение для времени может иметь некоторые другие компоненты: например, оно может иметь некоторое постоянное время запуска; но эти другие компоненты бледнеют к незначительности для больших значений n, а a*log (n) является доминирующим термином для больших n.

обратите внимание, что если бы уравнение было, например ...

Время (n) = a + blog (n) + cn + dnn

... тогда это будет O (N в квадрате), потому что, независимо от значений констант a, b, c и ненулевых d,d*n*n термин всегда будет доминировать над другим для любого достаточно большого значения n.

вот что означает обозначение bit O: это означает " каков порядок доминирующего термина для любого достаточно больших n".

Я могу добавить кое-что интересное, что я прочитал в книге Кормена и т. д. давным-давно. Теперь представьте себе проблему, где мы должны найти решение в проблемном пространстве. Это проблемное пространство должно быть конечным.

теперь, если вы можете доказать, что на каждой итерации вашего алгоритма вы отрезаете часть этого пространства, то есть не меньше некоторого предела, это означает, что ваш алгоритм работает в O(logN) времени.

Я должен отметить, что мы говорим здесь о предел относительной доли, а не абсолютной. Классический пример-бинарный поиск. На каждом шаге мы выбрасываем 1/2 проблемного пространства. Но binary search-не единственный такой пример. Предположим, вы каким-то образом доказали, что на каждом шаге выбрасываете не менее 1/128 проблемного пространства. Это означает, что ваша программа все еще работает в O(logN) время, хотя значительно медленнее, чем двоичный поиск. Это очень хороший намек при анализе рекурсивных алгоритмов. Часто можно доказать, что у каждого шаг рекурсия не будет использовать несколько вариантов, и это приводит к отсечению некоторой доли в проблемном пространстве.

log x to base b = y обратное b^y = x

Если у вас есть m-арное дерево глубины d и размера n, то:

• пересечение всего дерева ~ O (M^d) = O(n)

• прогулка по одному пути в дереве ~ O (d) = O(log n to base M)

Я могу привести пример для цикла for и, возможно, когда-то понял концепцию, возможно, будет проще понять в разных контекстах.

это означает, что в цикле шаг растет экспоненциально. Е. Г.

for (i=1; i<=n; i=i*2) {;}

сложность в o-нотации этой программы-O (log (n)). Давайте попробуем пройти через него вручную (n находится где-то между 512 и 1023 (исключая 1024):

step: 1   2   3   4   5    6    7    8     9     10
   i: 1   2   4   8   16   32   64   128   256   512

хотя n находится где-то между 512 и 1023, только 10 итераций проходить. Это связано с тем, что шаг в цикле растет экспоненциально и, таким образом, занимает всего 10 итераций для достижения завершения.

логарифм x (к основанию a) является обратной функцией a^x.

Это как сказать, что логарифм является обратной показательной.

теперь попробуйте увидеть это таким образом, если экспоненциальный растет очень быстро, то логарифм растет (наоборот) очень медленно.

разница между O (n) и O(log(n)) огромен, подобно разнице между O(n) и O (a^n) (a-константа).

в информационных технологиях это означает, что:

  f(n)=O(g(n)) If there is suitable constant C and N0 independent on N, 
  such that
  for all N>N0  "C*g(n) > f(n) > 0" is true.

Ant похоже, что эта нотация была в основном взята из математики.

в этой статье есть цитата: D. E. кнут, "большой Омикрон и большая Омега и большая тета", 1976:

на основе вопросов, обсуждаемых здесь, я предлагаю членам SIGACT и редакторы журналов по информатике и математике, примите обозначения, как определено выше, если a лучшей альтернативой может быть найдено достаточно скоро.

сегодня 2016, но мы используем его по-прежнему сегодня.

в математическом анализе это означает, что:

  lim (f(n)/g(n))=Constant; where n goes to +infinity

но даже в математическом анализе иногда этот символ использовался в значении "C*g(n) > f (n) > 0".

Как я знаю из Университета, символ был intoduced немецким математиком Ландау (1877-1938)

на самом деле, если у вас есть список из n элементов и создайте двоичное дерево из этого списка (как в алгоритме divide and conquer), вы будете продолжать делить на 2, пока не достигнете списков размера 1 (Листья).

на первом шаге вы делите на 2. Затем у вас есть 2 списка (2^1), вы делите каждый на 2, поэтому у вас есть 4 списка (2^2), вы снова делите, у вас есть 8 списков (2^3)и так далее, пока ваш размер списка не будет 1

это дает вам уравнение :

n/(2^steps)=1 <=> n=2^steps <=> lg(n)=steps

(вы берете lg каждой стороны, lg является базой журнала 2)

полным двоичным примером является O( ln n), потому что поиск выглядит следующим образом:

1 2 3 4 5 6 7 8 9 10 11 12

Поиск 4 дает 3 попадания: 6, 3, затем 4. И log2 12 = 3, что является хорошим apporximate к тому, сколько хитов, где это необходимо.

Если вы ищете ответ на основе интуиции, я хотел бы предложить вам две интерпретации.

1. представьте себе очень высокий холм с очень широким основанием. Чтобы достичь вершины холма, есть два пути: один-это выделенная тропа, идущая по спирали вокруг холма, достигающая вершины, другой: небольшая терраса, похожая на резьбу, вырезанную для обеспечения лестницы. Теперь, если первый способ достигает в линейное время O (n), второй-O (log северный.)

2. представьте себе алгоритм, который принимает целое число, n как вход и завершается во времени, пропорциональном n тогда это O(n) или theta (n), но если он работает во времени пропорционально number of digits or the number of bits in the binary representation on number затем алгоритм выполняется в O (log n) или тета(log n) времени.

каждый раз, когда мы пишем алгоритм или код, мы попытаемся проанализировать его асимптотическую сложность. Он отличается от своего сложность.

асимптотическая сложность-это поведение времени выполнения алгоритма, а временная сложность-фактическое время выполнения. Но некоторые люди используют эти термины взаимозаменяемо.

потому что сложность зависит от различных параметров, а именно.
1. Физическая Система
2. Программирование Язык
3. стиль кодирования
4. И многое другое ......

фактическое время выполнения не является хорошей мерой для анализа.

вместо этого мы берем размер ввода в качестве параметра, потому что любой код, ввод же. таким образом, время выполнения является функцией размера ввода.

Ниже приведен пример алгоритма Линейного Времени

линейный Поиск
учитывая n входных элементов, для поиска элемента в массиве вам нужно не более' n ' сравнения. Другими словами, независимо от того, какой язык программирования вы используете, какой стиль кодирования вы предпочитаете, на какой системе вы его выполняете. В худшем случае требуется только n сравнений.Время выполнения линейно пропорционально размеру входных данных.

и его не просто поиск, какой бы ни была работа (инкремент, сравнение или любая операция) его функция размер входного сигнала.

поэтому, когда вы говорите, что любой алгоритм O (log n) это означает, что время выполнения журнала раз входной размер n.

по мере увеличения размера ввода увеличивается выполненная работа (здесь время выполнения).(Отсюда пропорциональность)

      n      Work
      2     1 units of work
      4     2 units of work
      8     3 units of work

см. как увеличенный размер входного сигнала проделанная работа увеличена и она независима от любой машины. А если попытаться выяснить ценность единиц труда На самом деле это зависит от указанных выше параметров.Это будет изменения в соответствии с системами и все такое.

Я хотел бы добавить, что высота дерева-это длина самого длинного пути от корня до листа, и что высота узла-это длина самого длинного пути из этого узла до листа. Путь означает количество узлов, с которыми мы сталкиваемся при пересечении дерева между двумя узлами. Для достижения сложности времени O (log n) дерево должно быть сбалансировано, что означает, что разница высоты между дочерними элементами любого узла должна быть меньше или равна 1. Следовательно, деревья не всегда гарантируют временную сложность O (log n), если они не сбалансированы. На самом деле в некоторых случаях, временная сложность поиска в дереве может быть o(n) в худшем случае.

вы можете взглянуть на деревья баланса, такие как AVL tree. Это работает над балансировкой дерева при вставке данных, чтобы сохранить временную сложность (log n) при поиске в дереве.