я предполагаю, что вы определили собственные векторы из eigth собственное значение, видели в D.

Однако собственные значения находятся в диагональной матрице, поэтому мы извлекаем диагонали с помощью diag команда, сортировать их и выяснить их порядок, а затем изменить A уважать этот заказ. Я использую второй вывод sort потому что он сообщает вам позицию, где каждое значение в несортированном результате появится в отсортированном результате. Это заказ нужно переставить столбцы матрицы собственных векторов A. Очень важно, чтобы вы выбрали 'descend' как флаг, так что наибольшее собственное значение и связанный с ним собственный вектор появляются первыми, как мы говорили раньше.

затем вы можете вырвать первый k самые большие векторы и значения через:

k = 800;
Aq = Asort(:,1:k);

Вопрос № 2

хорошо известно, что собственные векторы ковариационной матрицы равны основным компонентам. Конкретно, первый главный компонент (т. е. самый большой собственный вектор и связанное с ним самое большое собственное значение) дает вам направление максимальная вариабельность в ваших данных. Каждый основной компонент после этого дает вам изменчивость уменьшающегося характера. Также хорошо отметить, что каждый основной компонент ортогональных друг к другу.

вот хороший пример из Википедии для двумерных данных:

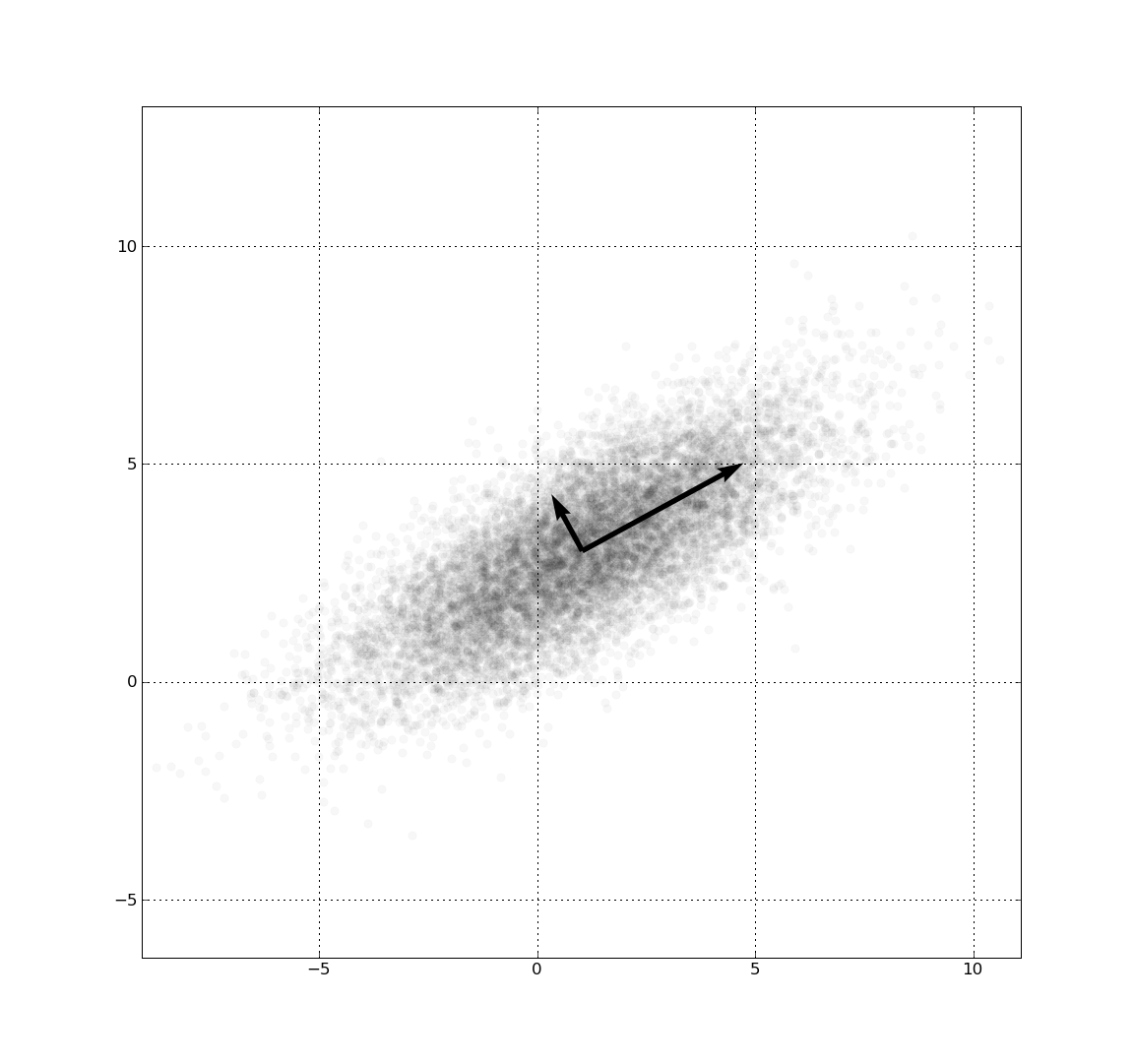
я вытащил выше изображение из статьи Википедии по анализу основных компонентов, с которой я связал вас выше. Это диаграмма рассеяния выборок, распределенных в соответствии с двумерным гауссовым распределением с центром (1,3) со стандартным отклонением 3 примерно в (0.878, 0.478) направлении и 1 в ортогональном направлении. Компонент со стандартным отклонением 3 является первым основным компонентом, а ортогональный-вторым компонентом. Указанные векторы собственные векторы ковариационной матрицы масштабируются квадратным корнем соответствующего собственного значения и смещаются так, что их хвосты находятся в среднем.

теперь давайте вернемся к вашему вопросу. Причина, по которой мы смотрим на k самые большие собственные значения-это способ выполнения сокращение размерности. По сути, вы будете выполнять сжатие данных, где вы возьмете свои данные более высоких измерений и проецировать их на пространство более низких измерений. Чем больше основные компоненты, которые вы включаете в свою проекцию, тем больше будут напоминать исходные данные. В какой-то момент он начинает сходить на нет, но первые несколько основных компонентов позволяют по большей части точно восстановить данные.

отличный визуальный пример выполнения PCA (или SVD, скорее) и восстановления данных найден этим великим сообщением Quora, на которое я наткнулся в прошлое.

http://qr.ae/RAEU8a

Вопрос #3

вы бы использовали эту матрицу для перепроектирования ваших данных более высоких измерений в пространство более низких измерений. Число строк 1000 все еще существует, что означает, что в вашем наборе данных изначально было 1000 объектов. 800 - это то, что уменьшит размерность ваших данных. Рассмотрим эту матрицу как преобразование из исходной размерности объекта (1000) вниз к своей уменьшенной размерности (800).

затем вы должны использовать эту матрицу в сочетании с реконструкция каковы были исходные данные. Конкретно, это даст вам приблизительное представление о том, как выглядели исходные данные с наименьшей ошибкой. В этом случае вам не нужно использовать все основные компоненты (т. е. просто k самые большие векторы), и вы можете создать аппроксимацию ваших данных с меньшим количеством информации, чем у вас было до.

как вы восстанавливаете свои данные очень просто. Давайте сначала поговорим о прямых и обратных операциях с полными данными. Передовая операция-взять исходные данные и перепроектировать их, но вместо более низкой размерности мы будем использовать все компонентов. Сначала вам нужно иметь исходные данные, но среднее значение вычитается:

Bm = bsxfun(@minus, B, mean(B,1));

Bm создаст матрицу, в которой каждая особенность каждого образца будет вычитаться. bsxfun позволяет вычитание двух матриц в неравной размерности при условии, что вы можете эфир размеры, чтобы они могли совпадать. В частности, в этом случае произойдет то, что среднее значение каждого столбца / функции и будет создана временная реплицированная матрица размером B. Когда вы вычитаете исходные данные с помощью этой реплицированной матрицы, эффект вычитает каждую точку данных с помощью их особенность означает, что децентрализация данных, что означает каждая характеристика равна 0.

как только вы это сделаете, операция для проекта просто:

Bproject = Bm*Asort;

вышеуказанная деятельность довольно проста. То, что вы делаете, выражает функцию каждого образца как линейную комбинацию основных компонентов. Например, учитывая первый образец или первую строку децентрализованных данных, функция первого образца в Проектируемом домене является точечным продуктом вектор строки, который относится ко всей выборке и первому основному компоненту, который является вектором столбца.. Второй особенностью первого образца в проектируемой области является взвешенная сумма всей выборки и второго компонента. Вы повторите это для всех образцов и всех основных компонентов. Фактически, вы перепроектируете данные так, чтобы это было относительно основных компонентов-ортогональных базисных векторов, которые преобразуют ваши данные из одного представления в другой.

лучшее описание того, о чем я только что говорил, можно найти здесь. Посмотрите на ответ Амро:

анализ главных компонент Matlab (порядок собственных значений)

теперь, чтобы вернуться назад, вы просто делаете обратную операцию, но специальное свойство с собственной матрицей вектора заключается в том, что если вы транспонируете это, вы получаете обратное. Чтобы вернуть исходные данные, отмените операцию выше и добавьте средства обратно в проблема:

out = bsxfun(@plus, Bproject*Asort.', mean(B, 1));

вы хотите получить исходные данные обратно, поэтому вы решаете для Bm относительно предыдущей операции, которую я сделал. Однако, обратное Asort просто перенести сюда. То, что происходит после выполнения этой операции, заключается в том, что вы возвращаете исходные данные, но данные все еще децентрализованы. Чтобы вернуть исходные данные, необходимо добавить средства каждого объекта обратно в матрицу данных для получения конечного результата. Вот почему мы используем другое bsxfun вызовите здесь, чтобы вы могли сделать это для значений функций каждого образца.

вы должны быть в состоянии вернуться назад и вперед от исходного домена и проецируемого домена с вышеуказанными двумя строками кода. Теперь, когда уменьшение размерности (или приближение исходных данных) вступает в игру, это обратная операция. Сначала вам нужно спроецировать данные на базы основных компонентов (т. е. на прямую операцию), но теперь идти в исходном домене, где мы пытаемся восстановить данные с уменьшенным количеством основных компонентов, вы просто замените Asort в приведенном выше коде с Aq, а также уменьшить количество функций, которые вы используете в Bproject. Конкретно:

out = bsxfun(@plus, Bproject(:,1:k)*Aq.', mean(B, 1));

делаешь Bproject(:,1:k) выбирает из k особенности в проектируемой области ваших данных, соответствующие k большой векторами. Интересно, если вы просто хотите представление данных что касается уменьшенной размерности, вы можете просто использовать Bproject(:,1:k) и этого будет достаточно. Однако, если вы хотите пойти вперед и вычислить аппроксимацию исходных данных, нам нужно вычислить обратный шаг. Приведенный выше код-это просто то, что мы имели раньше с полной размерностью ваших данных, но мы используем Aq а также выбор из k функции Bproject. Это даст вам исходные данные, которые представлены k самые большие собственные векторы / собственные значения в твоей матрице.

если вы хотите увидеть удивительный пример, я буду имитировать сообщение Quora, которое я связал с вами, но используя другое изображение. Подумайте об этом с изображением в оттенках серого, где каждая строка является "образцом", а каждый столбец-функцией. Давайте возьмем изображение оператора, которое является частью панели инструментов обработки изображений:

im = imread('camerman.tif');
imshow(im); %// Using the image processing toolbox

мы получаем такое изображение:

это изображение 256 x 256, что означает, что у нас есть 256 точек данных, и каждая точка имеет 256 особенности. Что я собираюсь сделать, это преобразовать изображение в double для точности вычисления ковариационной матрицы. Теперь я собираюсь повторить приведенный выше код, но постепенно увеличивая k на каждый из 3, 11, 15, 25, 45, 65 и 125. Поэтому для каждого k, мы вводим больше основных компонентов, и мы должны медленно начать получать реконструкцию наших данных.

вот некоторый runnable код, который иллюстрирует мою мысль:

%%%%%%%// Pre-processing stage
clear all;
close all;

%// Read in image - make sure we cast to double
B = double(imread('cameraman.tif'));

%// Calculate covariance matrix
sigma = cov(B);

%// Find eigenvalues and eigenvectors of the covariance matrix
[A,D] = eig(sigma);
vals = diag(D);

%// Sort their eigenvalues
[~,ind] = sort(abs(vals), 'descend');

%// Rearrange eigenvectors
Asort = A(:,ind);

%// Find mean subtracted data
Bm = bsxfun(@minus, B, mean(B,1));

%// Reproject data onto principal components
Bproject = Bm*Asort;

%%%%%%%// Begin reconstruction logic
figure;
counter = 1;

for k = [3 11 15 25 45 65 125 155]
    %// Extract out highest k eigenvectors
    Aq = Asort(:,1:k);

    %// Project back onto original domain
    out = bsxfun(@plus, Bproject(:,1:k)*Aq.', mean(B, 1));

    %// Place projection onto right slot and show the image
    subplot(4, 2, counter);
    counter = counter + 1;
    imshow(out,[]);
    title(['k = ' num2str(k)]);
end

как вы можете видеть, большая часть кода совпадает с тем, что мы видели. Разница в том, что я перебираю все значения k проект обратно в исходное пространство (т. е. вычисление приближения) с k самые высокие собственные векторы, затем покажите изображение.

получаем такую милую цифру:

как вы можете видеть, начиная с k=3 не у нас любые услуги... мы можем видеть некоторую общую структуру,но не повредит добавить больше. По мере увеличения количества компонентов мы начинаем получать более четкое представление о том, как выглядят исходные данные. At k=25, мы действительно можем видеть, как выглядит оператор, и нам не нужны компоненты 26 и выше, чтобы увидеть, что происходит. Это то, о чем я говорил в отношении сжатия данных, где вам не нужно работать со всеми основными компонентами, чтобы получить четкое представление картина того, что происходит.

я хотел бы закончить эту заметку, обратив вас к замечательной экспозиции Криса Тейлора на тему анализа основных компонентов, с кодом, графиками и отличным объяснением для загрузки! Здесь я начал работать над PCA, но сообщение Quora-это то, что укрепило мои знания.

Matlab-PCA анализ и реконструкция многомерных данных