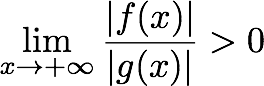Что такое сублинейные алгоритмы?

один из моих товарищей задал мне следующий вопрос.

Which of the following expressions is not sublinear?
O(log log n)
O(n)
O(logn)
O(root(n))

Я прошел через https://en.wikipedia.org/wiki/Time_complexity#Sub-linear_time но не мог, но я не уверен, что понял это полностью. Кто-нибудь может указать мне правильное направление.

10
algorithm asymptotic-complexity limits

2 ответов

функция f(x), как говорят, растет быстрее, чем другая функция, g (x), если предел их отношений по мере приближения X к бесконечности переходит к некоторому положительному, ограниченному числу, как показано в определении ниже.

enter image description here

в случае сублинейного мы хотим доказать, что функция растет медленнее, чем c*n, где c-некоторое положительное число.

таким образом, для каждой функции f(n) в вашем списке мы хотим соотношение f(n) к (c*n). Если лимит 0, это означает, что функция f (n) является сублинейной. В противном случае он растет с той же (приблизительной) скоростью n или быстрее.

lim n->inf (log log n)/(c*n) = 0 (via l'Hopital's)

(сублинейное)

lim n->inf (n)/(c*n) = 1/c != 0

(линейные)

lim n->inf (log n)/(c*n) = 0 (via l'Hopital's)

(сублинейное)

lim n->inf (sqrt(n))/(c*n) = 0

(сублинейное)

14

думаю, я понял, почему вы смущены: страница Википедии, которую вы используете Мало-О Примечание:

суб-линейного времени

алгоритм, как говорят, работает в сублинейное время (часто пишется сублинейное время), если T(n) = o (n)

остерегайтесь, что T(n) = o (n) является сильнее требование, чем говорить T(n) = O (n).

в частности, для функции в O (n) вы не всегда можете иметь неравенство 

f(x) < k g(x) for all x > a

удовлетворены для каждого k вы выберете. y=x и k=1 докажет вам неправоту и мало-о нотации требует каждый k для удовлетворения этого выражения.

любая функция O(n) является не также в o (n). Таким образом, ваше не-сублинейное выражение-O(n).

рекомендую почитать ответ продолжить учебу

9