De Bruijn алгоритм двоичный счетчик цифр 64bits C#
Im, используя алгоритм "De Bruijn", чтобы обнаружить количество цифр в двоичном файле, которое имеет большое число (до 64 бит).
например:
- 1022 имеет 10 цифр в двоичном формате.
- 130 имеет 8 цифр в двоичной системе.
я обнаружил, что использование поиска таблицы на основе De Bruijn дает мне возможность вычислить этот x100 раз быстрее, чем обычные способы (мощность, квадрат,...).
по данным этот сайт, 2^6 имеет таблицу для вычисления 64-битных чисел. это будет таблица, представленная в c#
static readonly int[] MultiplyDeBruijnBitPosition2 = new int[64]
{
0,1,2,4,8,17,34,5,11,23,47,31,63,62,61,59,
55,46,29,58,53,43,22,44,24,49,35,7,15,30,60,57,
51,38,12,25,50,36,9,18,37,10,21,42,20,41,19,39,
14,28,56,48,33,3,6,13,27,54,45,26,52,40,16,32
};
(Я не знаю, правильно ли я принес таблицу с этого сайта) Затем, основываясь на р.. комментарий здесь. Я должен использовать это, чтобы использовать таблицу с входным номером uint64.
public static int GetLog2_DeBruijn(ulong v)
{
return MultiplyDeBruijnBitPosition2[(ulong)(v * 0x022fdd63cc95386dull) >> 58];
}
но компилятор c# не позволяет мне использовать "0x022fdd63cc95386dull " потому что он переполняет 64bits. И я должен использовать "0x022fdd63cc95386d" вместо этого.
используя эти коды. Проблема в том, что я не получаю правильный результат для заданных входных.
например, выполнение 1.000.000 вычислений числа: 17012389719861204799 (используется 64 бит) это результат:
- используя метод pow2 я получаю результат 64 1 миллион раз в 1380ms.
- используя метод DeBruijn, я получаю результат 40 1 миллион раз в 32 МС. (Не знаю почему. 40)
Я пытаюсь понять, как работает "De Bruijn", и как я могу это исправить и создать окончательный код для c# для вычисления чисел до 64 бит.
UDPATE и эталоны различных решений
Я искал самый быстрый алгоритм, чтобы получить количество цифр в двоичном файле, которое беззнаковое заданное число 64bits имеет в c# (известном как ulong).
например:
- 1024 имеет 11 двоичных цифр. (2^10+1) или (log2[1024]+1)
- 9223372036854775808 имеет 64 двоичных числа. (2^63+1) или (log2[2^63]+1)
обычная сила 2 и квадрата весьма медленна. и как раз для 10000 вычислений для этого нужно 1500ms получить ответ. (Расчеты 100M требуют часов).
здесь Никлас Б., Джим Германии и расточитель принес различные методы, чтобы сделать это быстрее.
- SIMD и SWAR Техника / / предоставлено Spender (ответ здесь)
- De_Bruijn Splited 32bits / / предоставлено Джимом Мишелем (ответ здесь)
- версия De_Bruijn 64bits / / предоставлено Никласом Б. (ответ здесь)
- De_Bruijn 128bits version / / также предоставлены Niklas B. (ответ здесь)
тестирование этих методов с процессором Q6600, разогнанным до 3 ГГц с помощью Windows 7 (64bits), дает следующие результаты.
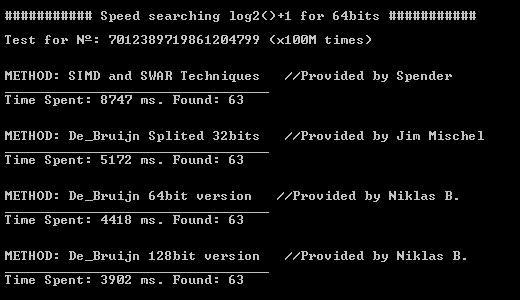
Как вы можете видеть, требуется всего несколько секунд, чтобы найти правильно 100,000,000 запроса, будучи De_Bruijn 128bits версии быстрее.
большое спасибо всем вам, вы мне очень помогаете в этом. Надеюсь, тебе это тоже поможет.
4 ответов
вы должны проверить Р..'ы ответ и его ресурс снова. Вопрос, на который он ответил, состоял в том, как найти log2 для полномочия двух.
на веб-сайте bit twiddling говорится, что простое умножение + сдвиг работает только "если вы знаете, что v-это сила 2". В противном случае вам нужно округлить до следующей степени двойки первый:
static readonly int[] bitPatternToLog2 = new int[64] {
0, // change to 1 if you want bitSize(0) = 1
1, 2, 53, 3, 7, 54, 27, 4, 38, 41, 8, 34, 55, 48, 28,
62, 5, 39, 46, 44, 42, 22, 9, 24, 35, 59, 56, 49, 18, 29, 11,
63, 52, 6, 26, 37, 40, 33, 47, 61, 45, 43, 21, 23, 58, 17, 10,
51, 25, 36, 32, 60, 20, 57, 16, 50, 31, 19, 15, 30, 14, 13, 12
}; // table taken from http://chessprogramming.wikispaces.com/De+Bruijn+Sequence+Generator
static readonly ulong multiplicator = 0x022fdd63cc95386dUL;
public static int bitSize(ulong v) {
v |= v >> 1;
v |= v >> 2;
v |= v >> 4;
v |= v >> 8;
v |= v >> 16;
v |= v >> 32;
// at this point you could also use popcount to find the number of set bits.
// That might well be faster than a lookup table because you prevent a
// potential cache miss
if (v == (ulong)-1) return 64;
v++;
return MultiplyDeBruijnBitPosition2[(ulong)(v * multiplicator) >> 58];
}
вот версия с большей таблицей поиска, которая позволяет избежать филиал и одно дополнение. Я нашел магическое число, используя случайный поиск.
static readonly int[] bitPatternToLog2 = new int[128] {
0, // change to 1 if you want bitSize(0) = 1
48, -1, -1, 31, -1, 15, 51, -1, 63, 5, -1, -1, -1, 19, -1,
23, 28, -1, -1, -1, 40, 36, 46, -1, 13, -1, -1, -1, 34, -1, 58,
-1, 60, 2, 43, 55, -1, -1, -1, 50, 62, 4, -1, 18, 27, -1, 39,
45, -1, -1, 33, 57, -1, 1, 54, -1, 49, -1, 17, -1, -1, 32, -1,
53, -1, 16, -1, -1, 52, -1, -1, -1, 64, 6, 7, 8, -1, 9, -1,
-1, -1, 20, 10, -1, -1, 24, -1, 29, -1, -1, 21, -1, 11, -1, -1,
41, -1, 25, 37, -1, 47, -1, 30, 14, -1, -1, -1, -1, 22, -1, -1,
35, 12, -1, -1, -1, 59, 42, -1, -1, 61, 3, 26, 38, 44, -1, 56
};
static readonly ulong multiplicator = 0x6c04f118e9966f6bUL;
public static int bitSize(ulong v) {
v |= v >> 1;
v |= v >> 2;
v |= v >> 4;
v |= v >> 8;
v |= v >> 16;
v |= v >> 32;
return bitPatternToLog2[(ulong)(v * multiplicator) >> 57];
}
вы должны обязательно проверить другие трюки для вычисления log2 и рассмотрите возможность использования MSR инструкция по монтажу если вы находитесь на x86(_64). Он дает вам индекс самого значительного бита набора, который именно то, что вам нужно.
после perusing различные бит-twiddling info, вот как я бы это сделал... не знаю, как это складывается рядом с DeBruijn, но должно быть значительно быстрее, чем использование полномочий.
ulong NumBits64(ulong x)
{
return (Ones64(Msb64(x) - 1ul) + 1ul);
}
ulong Msb64(ulong x)
{
//http://aggregate.org/MAGIC/
x |= (x >> 1);
x |= (x >> 2);
x |= (x >> 4);
x |= (x >> 8);
x |= (x >> 16);
x |= (x >> 32);
return(x & ~(x >> 1));
}
ulong Ones64(ulong x)
{
//https://chessprogramming.wikispaces.com/SIMD+and+SWAR+Techniques
const ulong k1 = 0x5555555555555555ul;
const ulong k2 = 0x3333333333333333ul;
const ulong k4 = 0x0f0f0f0f0f0f0f0ful;
x = x - ((x >> 1) & k1);
x = (x & k2) + ((x >> 2) & k2);
x = (x + (x >> 4)) & k4;
x = (x * 0x0101010101010101ul) >> 56;
return x;
}
когда я посмотрел на это некоторое время назад для 32 бит, метод последовательности DeBruijn был намного быстрее. См.https://stackoverflow.com/a/10150991/56778
что можно сделать для 64 бит разбивается на два 32-битных значения. Если высокие 32 бита ненулевые, то запустите на нем расчет DeBruijn, а затем добавьте 32. Если высокие 32 бита равны нулю, выполните расчет DeBruijn на низких 32 битах.
что-то вроде этого:
int NumBits64(ulong val)
{
if (val > 0x00000000FFFFFFFFul)
{
// Value is greater than largest 32 bit number,
// so calculate the number of bits in the top half
// and add 32.
return 32 + GetLog2_DeBruijn((int)(val >> 32));
}
// Number is no more than 32 bits,
// so calculate number of bits in the bottom half.
return GetLog2_DeBruijn((int)(val & 0xFFFFFFFF));
}
int GetLog2_DeBruijn(int val)
{
uint32 v = (uint32)val;
int r; // result goes here
static const int MultiplyDeBruijnBitPosition[32] =
{
0, 9, 1, 10, 13, 21, 2, 29, 11, 14, 16, 18, 22, 25, 3, 30,
8, 12, 20, 28, 15, 17, 24, 7, 19, 27, 23, 6, 26, 5, 4, 31
};
v |= v >> 1; // first round down to one less than a power of 2
v |= v >> 2;
v |= v >> 4;
v |= v >> 8;
v |= v >> 16;
r = MultiplyDeBruijnBitPosition[(uint32_t)(v * 0x07C4ACDDU) >> 27];
return r;
}
Edit: это решение не рекомендуется, поскольку оно требует ветвления для нуля.
после прочтения ответ Никласа Б Я потратил несколько часов на исследование этого, и понимаю, что весь волшебный мультипликатор должен быть в последнем nth, чтобы удовлетворить 64-элементной таблице поиска (у меня нет необходимых знаний, чтобы объяснить, почему).
поэтому я использовал точно такой же генератор упоминается в этом ответе, чтобы найти последние последовательность, вот это C# код:
// used generator from http://chessprogramming.wikispaces.com/De+Bruijn+Sequence+Generator
static readonly byte[] DeBruijnMSB64table = new byte[]
{
0 , 47, 1 , 56, 48, 27, 2 , 60,
57, 49, 41, 37, 28, 16, 3 , 61,
54, 58, 35, 52, 50, 42, 21, 44,
38, 32, 29, 23, 17, 11, 4 , 62,
46, 55, 26, 59, 40, 36, 15, 53,
34, 51, 20, 43, 31, 22, 10, 45,
25, 39, 14, 33, 19, 30, 9 , 24,
13, 18, 8 , 12, 7 , 6 , 5 , 63,
};
// the cyclc number has to be in the last 16th of all possible values
// any beyond the 62914560th(0x03C0_0000) should work for this purpose
const ulong DeBruijnMSB64multi = 0x03F79D71B4CB0A89uL; // the last one
public static byte GetMostSignificantBit(this ulong value)
{
value |= value >> 1;
value |= value >> 2;
value |= value >> 4;
value |= value >> 8;
value |= value >> 16;
value |= value >> 32;
return DeBruijnMSB64table[value * DeBruijnMSB64multi >> 58];
}
