Динамическое программирование на деревьях C модификациями
недавно я прочитал проблему на деревьях, но мне было трудно подойти к этой проблеме. Вот проблема:
есть страна с n городов (от 2 до 10^5) и (n-1) двунаправленные дороги, такие, что можно путешествовать между любой парой городов. У нас есть 1 волшебный грузовик, который может путешествовать между городами, но на это потребуется 1 единица времени (если он загружен) и 0 единичное время (если не загружено) in путешествие между соседними городами, и смогите держать на максимальном 1 блоке продукта.
теперь вы можете иметь клиента в любом городе, который требует ровно 2 единицы продукции и более 2 единиц времени.
теперь вопрос в том, что мы должны минимизировать общее количество складов с заданными ограничениями:
- город не может иметь более одного хранилища.
- хранилище может хранить только 1 единицы продукции.
назначьте хранилища в стране так, чтобы вы можете заполнить по крайней мере первый заказ вовремя. Учитывая, что заказ может быть размещен в любом городе.
ограничение по времени: 1sec
что я пробовал:
худший подход, который я могу думать, это грубая сила. Попробуйте разместить хранилище в каждом городе (2^n возможностей) и проверить, может ли каждый городской заказ быть выполнен с помощью соседних городов. Но временная сложность этого будет (n * 2^n). Так не получится вообще.
второй подход, я думаю, использует DP на деревьях как-то. И я также не уверен, будет ли это оптимальным. Из выше проблемы я могу гарантировать, что листья должны иметь 1 хранилище наверняка. и я думал, что DP, как, начните с корня и проверьте, могут ли дети помочь в выполнении его заказа и назначить хранение этому городу соответственно, с базовым случаем на листьях. Но проблема здесь что дети также могут выполнять заказ от родителя, поэтому он делает круговые петли. Так что мне это тоже не помогло.
последний подход я думал применить двоичный поиск по самому ответу. Поскольку ответ может находиться между(1, n), то ответ можно найти в порядке nLog(n). Но опять же проблема в том, что я не мог придумать оптимальный способ назначения хранилищ в городах с заданным количеством хранилищ.
Итак, вот оно.. Я старался изо всех сил, но не мог решить эту проблему. Любой помощь будет оценена по достоинству. :)
примечание: Я не знаю, почему они делают постановку проблемы настолько сложная как это. Они могли бы легко объяснить проблему гораздо проще. В результате я больше не могу найти эту проблему в интернете. Это было где-то на Codeforces, я думаю.
1 ответов
важно отметить, что на графике есть n городов и N-1 дорог, и все города достижимы; это означает, что:
- нет циклических путей.
- есть, по крайней мере, 2 города с одной связью (конечные точки).
есть две возможности для каждого города; либо:
- в городе есть хранилище, а другое хранилище находится максимум в 2 городах.
- город нет хранилища, и подключен по крайней мере к двум городам, которые имеют хранилище.
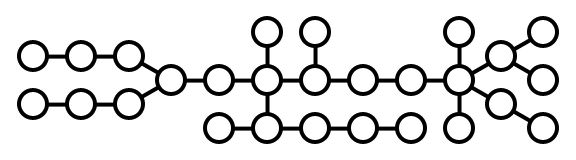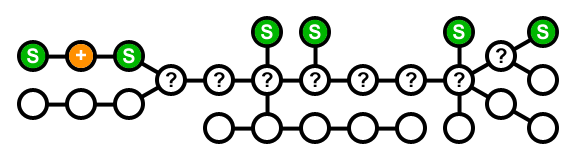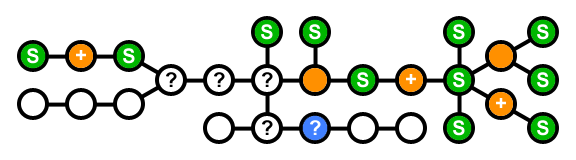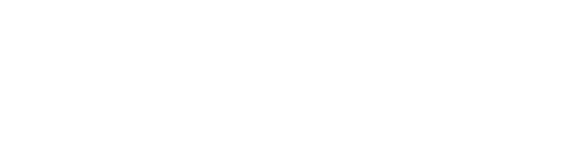
Это также означает, что односвязный город (конечная точка дороги) всегда имеет складское помещение, а строка дважды связанных городов должна (оптимально) поочередно иметь складское помещение или нет, что даст нам отправную точку при принятии решения о том, где разместить складские помещения.
синий: текущая узел; зеленый: хранение; оранжевый: нет хранения; +: нужен другой сосед с хранилищем; ?: посетил, но еще не решил
это дает нам следующий алгоритм:
- сначала найдите конечную точку: начните с любого города и двигайтесь в любом направлении до тех пор, пока не окажешься в городе с одной связью.
- положить в хранилище в одиночку-город, а затем вернуться к предыдущий город, и отметьте дорогу в город, из которого вы пришли, как посетил.
- если в этом городе есть только одна неосвещенная дорога. неосвещенная дорога, оставляющая след из соседних городов с и без хранилище.
- если вы приезжаете в город, который имеет более одной не посещаемой дороги, подождите решите, поставить ли хранилище и взять любой из не посещенные дороги; позже, когда вы вернетесь в этот город, и он только одна не посещенная дорога, вы будете знать, есть ли уже посещенные соседние города требуют, чтобы этот город имел место хранения объект.
- делайте это, пока вы не окажетесь в городе без непрошеных дорог; это значит, вы прошли через весь график.
это в основном алгоритм "проехать по всем дорогам и снова вернуться", поэтому количество посещенных узлов составляет 2×N, а сложность-линейная или O (N).
стоит отметить, что порядок посещения городов не изменит результат, т. е. количество складских помещений, но может измениться некоторые из их местоположений. Рассмотрим эти два решения для 4-х городах:
S - / - S - S (solved left to right)
S - S - / - S (solved right to left)
приближаясь к фактическому коду, давайте посмотрим, что делать, как только вы определили конечную точку. Граф состоит из таких узлов, как, например, это:
NODE "city" C1
- neighbours: [C2, C4, C7]
- has_storage: undefined <- at first; will be set to true/false
- needs_more_storage: true/false <- we'll add this property as we go
- visited: true/false <- we'll add this property as we go
мы начинаем с конечной точки, а затем для каждого узла мы:
- отметьте узел как посещенный.
- посмотрите на соседние узлы: если вы найдете только один, который не определен, определите has_storage для текущий узел: если все соседи has_storage являются ложными или любой из соседей needs_more_storage истинно, установите текущий узел has_storage в true; если нет, установите has_storage false, и набор needs_more_storage true, если есть только один соседний город с хранилищем; затем перейдите к одному неопределенному соседу.
- если несколько соседних узлов не определены, перейдите к любому из них это незваный гость.
- если ни один из соседних узлов не определен, вы достигли последнего узла; это всегда конечная точка, поэтому установите ее has_storage к true; алгоритм теперь завершен.