Для чего окно Хэмминга?
Я работаю с некоторым кодом, который выполняет преобразование Фурье (для вычисления cepstrum образца звука). Прежде чем вычислить преобразование Фурье, он применяет окно Хэмминга к образцу:
for(int i = 0; i < SEGMENTATION_LENGTH;i++){
timeDomain[i] = (float) (( 0.53836 - ( 0.46164 * Math.cos( TWOPI * (double)i / (double)( SEGMENTATION_LENGTH - 1 ) ) ) ) * frameBuffer[i]);
}
почему он это делает? Я не могу найти никаких причин для этого в коде или в интернете.
4 ответов
всякий раз, когда вы делаете конечное преобразование Фурье, вы неявно применяете его к бесконечно повторяющемуся сигналу. Так, например, если начало и конец вашей конечной выборки не совпадают, это будет выглядеть как разрыв в сигнале и отображаться как много высокочастотной ерунды в преобразовании Фурье, чего вы на самом деле не хотите. И если ваш образец является красивым синусоидальным, но целое число периодов не вписывается точно в конечный образец, ваш FT будет показывать заметную энергию во всех местах, нигде не приближающихся к реальной частоте. Вы не хотите этого.
Windowing данные убеждается что концы соответствуют вверх пока держащ все разумно ровное; это значительно уменьшает вид "спектральной утечки" описанный в предыдущем абзаце.
Это старый вопрос, но я думал, что ответ может быть улучшена.
представьте, что сигнал, который вы хотите преобразовать Фурье, является чистой синусоидальной волной. В частотной области вы ожидаете, что он будет иметь резкий всплеск только на частоте синуса. Однако, если вы взяли преобразование Фурье, ваш хороший острый Спайк будет заменен чем-то вроде этого:
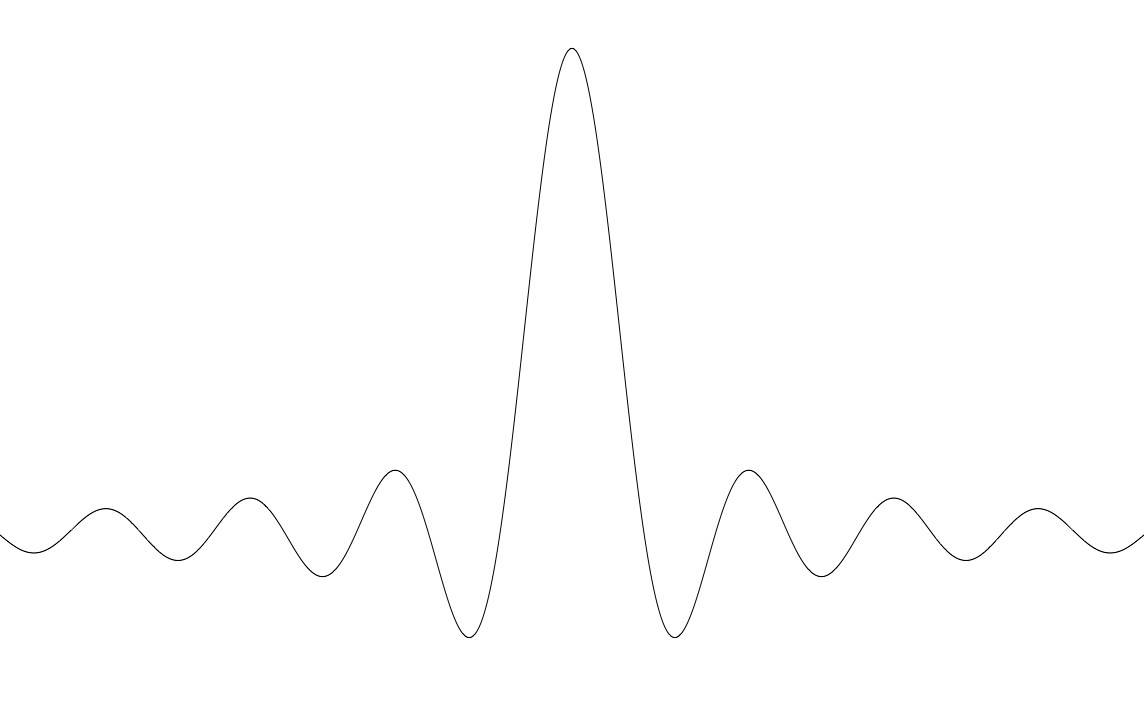
Почему это? Реальные синусоидальные волны простираются до бесконечности в обоих направлениях. Компьютеры невозможно выполнить вычисления с бесконечным числом точек данных, поэтому все сигналы "отрезаны" с обоих концов. Это вызывает рябь по обе стороны от пика, который вы видите. Окно Хэмминга уменьшает эту пульсацию, давая вам более точное представление о частотном спектре исходного сигнала.
больше теории, для заинтересованных: когда вы отключаете свой сигнал с обоих концов, вы неявно умножаете свой сигнал на квадратное окно. Фурье квадратное окно изображение выше, известный как функция sinc. Всякий раз, когда вы делаете преобразование Фурье на компьютере, нравится вам это или нет, вы всегда выбираете некоторые
с тем, что я знаю о звуке и быстрых исследованиях, похоже, что окно Хэмминга здесь, чтобы минимизировать боковую долю сигнала (нежелательное излучение). Таким образом, улучшается качество или гармоники звука. Я также понимаю этот тип функция окна подходит хорошо с DTFT.
вы найдете хорошее техническое объяснение на стэнфордский исследователь странице или Википедия, а также в документе Харрис Если вы готовы к математика :Д.
FT сегмента конечной длины синусоиды свертывает преобразование Фурье окна против пика частоты синусоиды, так как свойство FFT заключается в том, что векторное умножение в одной области является сверткой в другой. FT прямоугольного окна (что означает любую немодифицированную конечную длину образцов в БПФ) - это грязная функция Sinc, которая разбрызгивает любой сигнал, который не является точно периодическим в окне по всей частоте спектр.
FT окна в форме Хэмминга концентрирует это "брызги" намного ближе к пику частоты после свертки (чем функция Sinc), что приводит к более толстому, но более плавному пику частоты, но намного меньше брызг на частотах, далеких от пика частоты. Это приводит не только к более чистому спектру, но и к меньшим помехам от далеких частот на любом интересующем сигнале.
эта интерпретация (в отличие от " бесконечно повторение " интерпретация) делает более понятным, почему окна разной формы, чем Хэмминг, могут дать вам лучшие результаты с еще меньшей "утечкой". В частности, окно Хэмминга уменьшит размер первого бокового лепестка Sinc " утечки "рядом с пиком частоты в обмен на фактически большую" утечку " (или брызги свертки) далеко от интересующей частоты. Другие окна могут быть более подходящими, если вы хотите другой компромисс. Газета Харриса (pdf здесь) связанный в другом ответе выше, дает несколько примеров этих разных окон.
