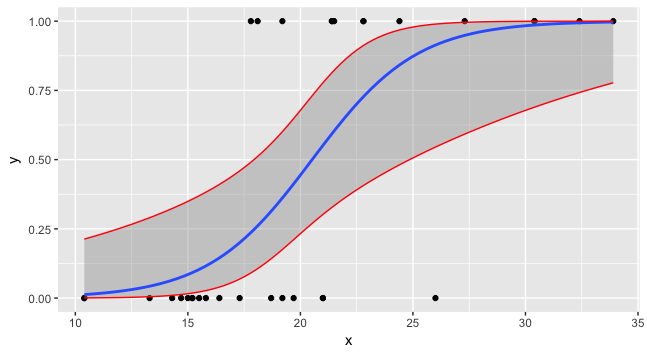
Доверительные интервалы для прогнозов логистической регрессии

в R предсказать.lm вычисляет предсказания на основе результатов линейной регрессии, а также предлагает вычислить доверительные интервалы для этих предсказаний. Согласно руководству, эти интервалы основаны на дисперсии погрешности подгонки, но не на интервалах погрешности коэффициента.

с другой стороны предсказать.glm, который вычисляет Прогнозы на основе логистической и пуассоновской регрессии (среди нескольких других), не имеет возможности для доверительных интервалов. И я даже трудно представить, как такие доверительные интервалы могут быть вычислены, чтобы обеспечить значимое понимание для Пуассона и логистической регрессии.

есть ли случаи, в которых имеет смысл предоставлять доверительные интервалы для таких прогнозов? Как их можно интерпретировать? И каковы предположения в этих случаях?

53
confidence-interval glm r statistics

1 ответов

обычный способ-вычислить доверительный интервал в масштабе линейного предиктора, где все будет более нормально (гауссово), а затем применить обратную функцию связи для отображения доверительного интервала от линейного предиктора к шкале ответа.

для этого нужно две вещи;

  1. вызов predict() С type = "link" и
  2. вызов predict() С se.fit = TRUE.

первый производит Прогнозы на шкала линейного предиктора, вторая возвращает стандартные ошибки предсказаний. В псевдо-коде

## foo <- mtcars[,c("mpg","vs")]; names(foo) <- c("x","y") ## Working example data
mod <- glm(y ~ x, data = foo, family = binomial)
preddata <- with(foo, data.frame(x = seq(min(x), max(x), length = 100)))
preds <- predict(mod, newdata = preddata, type = "link", se.fit = TRUE)

preds затем список с компонентами fit и se.fit.

доверительный интервал на линейном предикторе тогда

critval <- 1.96 ## approx 95% CI
upr <- preds$fit + (critval * preds$se.fit)
lwr <- preds$fit - (critval * preds$se.fit)
fit <- preds$fit

critval выбирается из t или z (нормальное) распределение по мере необходимости (я точно забыл, для какого типа GLM и какие свойства) с требуемым покрытием. The 1.96 является значением гауссова распределения, дающего 95% покрытия:

> qnorm(0.975) ## 0.975 as this is upper tail, 2.5% also in lower tail
[1] 1.959964

теперь fit, upr и lwr нам нужно применить к ним обратную функцию link.

fit2 <- mod$family$linkinv(fit)
upr2 <- mod$family$linkinv(upr)
lwr2 <- mod$family$linkinv(lwr)

теперь вы можете построить все три и данные.

preddata$lwr <- lwr2 
preddata$upr <- upr2 
ggplot(data=foo, mapping=aes(x=x,y=y)) + geom_point() +         
   stat_smooth(method="glm", method.args=list(family=binomial)) + 
   geom_line(data=preddata, mapping=aes(x=x, y=upr), col="red") + 
   geom_line(data=preddata, mapping=aes(x=x, y=lwr), col="red")

enter image description here

62