DSP-фильтрация в частотной области через FFT
я играл вокруг немного с реализацией Exocortex БПФ, но у меня возникли некоторые проблемы.
всякий раз, когда я изменяю амплитуды частотных бункеров перед вызовом iFFT, результирующий сигнал содержит некоторые щелчки и хлопки, особенно когда в сигнале присутствуют низкие частоты (например, барабаны или басы). Однако этого не происходит, если я ослабляю все бункеры одним и тем же фактором.
позвольте мне привести пример выходного буфера a 4-образец БПФ:
// Bin 0 (DC)
FFTOut[0] = 0.0000610351563
FFTOut[1] = 0.0
// Bin 1
FFTOut[2] = 0.000331878662
FFTOut[3] = 0.000629425049
// Bin 2
FFTOut[4] = -0.0000381469727
FFTOut[5] = 0.0
// Bin 3, this is the first and only negative frequency bin.
FFTOut[6] = 0.000331878662
FFTOut[7] = -0.000629425049
выход состоит из пар поплавков, каждый из которых представляет реальную и воображаемую части одного бункера. Таким образом, bin 0 (индексы массива 0, 1) будет представлять реальную и мнимую части частоты постоянного тока. Как вы можете видеть, бункеры 1 и 3 имеют одинаковые значения (за исключением знака части Im), поэтому я предполагаю, что bin 3 является первой отрицательной частотой, и, наконец, индексы (4, 5) будут последним положительным частотным бункером.
после этого ослабить частота bin 1 это то, что я делаю:
// Attenuate the 'positive' bin
FFTOut[2] *= 0.5;
FFTOut[3] *= 0.5;
// Attenuate its corresponding negative bin.
FFTOut[6] *= 0.5;
FFTOut[7] *= 0.5;
для фактических тестов я использую 1024-length FFT, и я всегда предоставляю все образцы, поэтому не требуется 0-padding.
// Attenuate
var halfSize = fftWindowLength / 2;
float leftFreq = 0f;
float rightFreq = 22050f;
for( var c = 1; c < halfSize; c++ )
{
var freq = c * (44100d / halfSize);
// Calc. positive and negative frequency indexes.
var k = c * 2;
var nk = (fftWindowLength - c) * 2;
// This kind of attenuation corresponds to a high-pass filter.
// The attenuation at the transition band is linearly applied, could
// this be the cause of the distortion of low frequencies?
var attn = (freq < leftFreq) ?
0 :
(freq < rightFreq) ?
((freq - leftFreq) / (rightFreq - leftFreq)) :
1;
// Attenuate positive and negative bins.
mFFTOut[ k ] *= (float)attn;
mFFTOut[ k + 1 ] *= (float)attn;
mFFTOut[ nk ] *= (float)attn;
mFFTOut[ nk + 1 ] *= (float)attn;
}
очевидно, я делаю что-то неправильно, но не могу понять, что.
Я не хочу использовать выход FFT в качестве средства для генерации набора коэффициентов FIR, так как я пытаюсь реализовать очень простой динамический эквалайзер.
каков правильный способ фильтрации в частотной домен? чего мне не хватает?
кроме того, действительно ли необходимо ослаблять отрицательные частоты? Я видел реализацию FFT, где neg. перед синтезом значения частоты обнуляются.
спасибо заранее.
4 ответов
есть две проблемы: как вы используете БПФ и конкретный фильтр.
фильтрация традиционно реализуется как свертка во временной области. Вы правы, что умножение спектров входного и фильтрующего сигналов эквивалентно. Однако, когда вы используете дискретное преобразование Фурье (DFT) (реализованное с алгоритмом быстрого преобразования Фурье для скорости), вы фактически вычисляете выборочную версию истинного спектра. Это имеет много последствий, но одним из наиболее важных для фильтрации является вывод о том, что сигнал временной области является периодическим.
вот пример. Рассмотрим синусоидальный входной сигнал x С 1,5 циклами в периоде, и простым фильтром нижних частот h. В синтаксисе Matlab/Octave:
N = 1024;
n = (1:N)'-1; %'# define the time index
x = sin(2*pi*1.5*n/N); %# input with 1.5 cycles per 1024 points
h = hanning(129) .* sinc(0.25*(-64:1:64)'); %'# windowed sinc LPF, Fc = pi/4
h = [h./sum(h)]; %# normalize DC gain
y = ifft(fft(x) .* fft(h,N)); %# inverse FT of product of sampled spectra
y = real(y); %# due to numerical error, y has a tiny imaginary part
%# Depending on your FT/IFT implementation, might have to scale by N or 1/N here
plot(y);
и вот график:
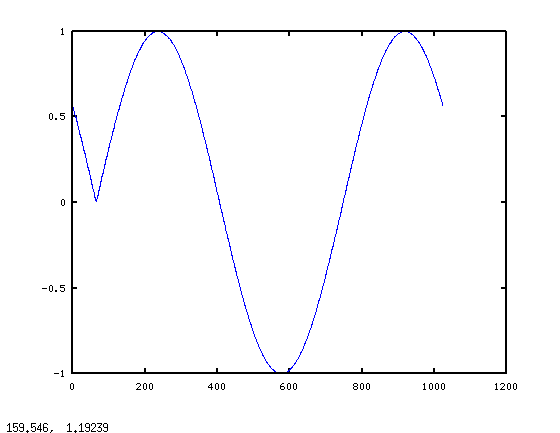
глюк в начале блока-это совсем не то, что мы ожидаем. Но если вы считаете fft(x), это имеет смысл. Дискретный Фурье Преобразование предполагает, что сигнал является периодическим внутри блока преобразования. Насколько известно DFT, мы попросили преобразовать один период этого:
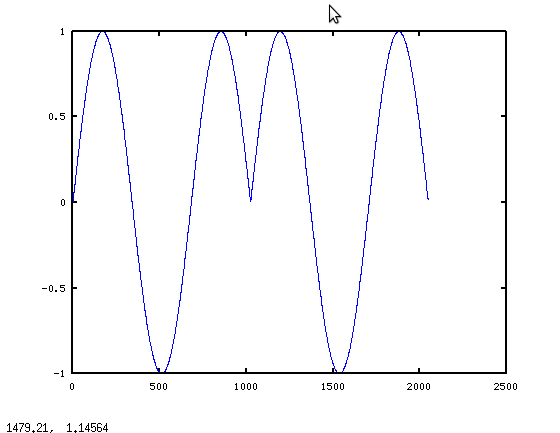
это приводит к первому важному соображению при фильтрации с помощью DFS: вы фактически реализуете круговой свертки, а не линейной свертки. Таким образом," глюк " на первом графике на самом деле не является глюком, когда вы рассматриваете математику. Итак, возникает вопрос: есть ли способ обойти периодичность? Ответ "да": используйте перекрытие-сохранение тегами. По сути, вы вычисляете N-длинные продукты, как указано выше, но сохраняете только N/2 пункта.
Nproc = 512;
xproc = zeros(2*Nproc,1); %# initialize temp buffer
idx = 1:Nproc; %# initialize half-buffer index
ycorrect = zeros(2*Nproc,1); %# initialize destination
for ctr = 1:(length(x)/Nproc) %# iterate over x 512 points at a time
xproc(1:Nproc) = xproc((Nproc+1):end); %# shift 2nd half of last iteration to 1st half of this iteration
xproc((Nproc+1):end) = x(idx); %# fill 2nd half of this iteration with new data
yproc = ifft(fft(xproc) .* fft(h,2*Nproc)); %# calculate new buffer
ycorrect(idx) = real(yproc((Nproc+1):end)); %# keep 2nd half of new buffer
idx = idx + Nproc; %# step half-buffer index
end
и вот график ycorrect:
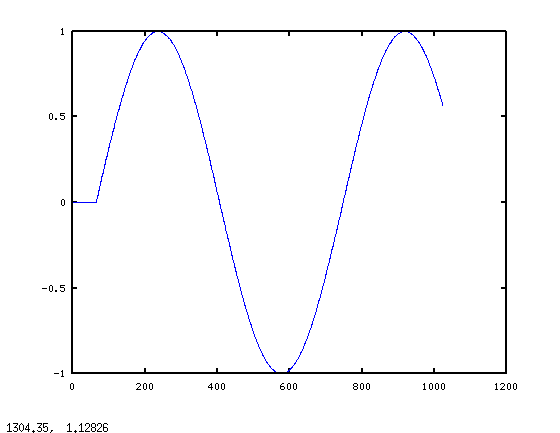
эта картина имеет смысл-мы ожидаем переходный процесс запуска от фильтра, затем результат оседает в стационарный синусоидальный отклик. Обратите внимание, что сейчас x можно сколь угодно долго. Ограничение Nproc > 2*min(length(x),length(h)).
теперь перейдем ко второму вопросу: конкретному фильтру. В вашем цикле вы создаете фильтр, спектр которого по существу H = [0 (1:511)/512 1 (511:-1:1)/512]'; если у вас hraw = real(ifft(H)); plot(hraw), вы получаете:
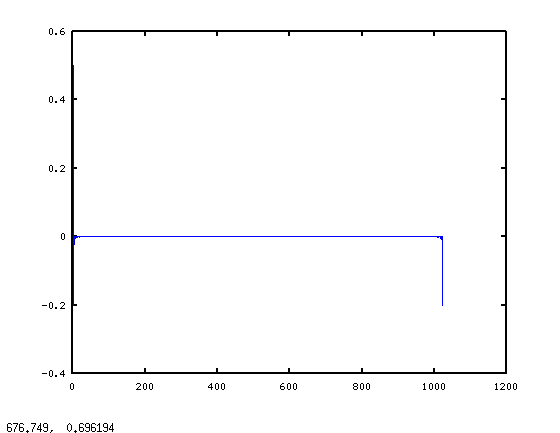
это трудно увидеть, но есть куча ненулевых точек на дальнем левом краю графика, а затем еще куча на дальнем правом краю. Используя Октавы встроенный
ваша основная проблема в том, что частоты не хорошо определены в течение коротких временных интервалов. Это особенно верно для низких частот, поэтому вы больше всего замечаете проблему.
поэтому, когда вы берете действительно короткие сегменты из звукового поезда, а затем фильтруете их, отфильтрованные сегменты не будут фильтровать таким образом, что создает непрерывную форму волны, и вы слышите прыжки между сегментами, и это то, что генерирует клики вы здесь.
например, принимая некоторые разумные числа: я начинаю с формы волны на 27,5 Гц (A0 на фортепиано), оцифрованной на 44100 Гц, это будет выглядеть так (где красная часть составляет 1024 образца):
alt текст http://i48.tinypic.com/zim802.png
Итак, сначала мы начнем с низкой частоты 40 Гц. Так как исходная частота меньше 40 Гц, фильтр нижних частот с отсечкой 40 Гц не должен иметь никакого эффекта, и мы получим выход это почти точно соответствует вводу. Правильно? неправильно, неправильно - и это в основном суть вашей проблемы. Проблема в том, что для коротких разделов идея 27.5 Гц не четко определен и не может быть хорошо представлен в DFT.
то, что 27,5 Гц не особенно значимо в коротком сегменте, можно увидеть, посмотрев на DFT на рисунке ниже. Обратите внимание, что, хотя DFT более длинного сегмента (черные точки) показывает пик в 27.5 Хз, короткий (красные точки) не делает.
alt текст http://i50.tinypic.com/14w6luw.png
ясно, тогда фильтровать под 40Hz, как раз захватит смещение DC, и результат фильтра нижних частот 40Hz показан в зеленом цвете ниже.
alt текст http://i48.tinypic.com/2vao21w.png
синяя кривая (взятая с выключением 200 Гц) начинает соответствовать намного лучше. Но обратите внимание, что это не низкие частоты, которые делают это хорошо, но включение высоких частот. Только когда мы включим все возможные частоты в короткий сегмент, до 22 кГц, мы, наконец, получим хорошее представление исходной синусоидальной волны.
причина всего этого в том, что небольшой сегмент синусоидальной волны 27,5 Гц является не синусоидальная волна 27,5 Гц, и это DFT не имеет большого отношения к 27,5 Гц.
вы ослабляете значение образца частоты постоянного тока до нуля? Похоже, что вы совсем не ослабляете его в своем примере. Поскольку вы реализуете фильтр высоких частот, вам также нужно установить значение DC в ноль.
это объясняет низкочастотные искажения. У вас будет много пульсаций в частотной характеристике на низких частотах, если это значение постоянного тока ненулевое из-за большого перехода.
вот пример в MATLAB / Octave для продемонстрируйте, что может произойти:
N = 32;
os = 4;
Fs = 1000;
X = [ones(1,4) linspace(1,0,8) zeros(1,3) 1 zeros(1,4) linspace(0,1,8) ones(1,4)];
x = ifftshift(ifft(X));
Xos = fft(x, N*os);
f1 = linspace(-Fs/2, Fs/2-Fs/N, N);
f2 = linspace(-Fs/2, Fs/2-Fs/(N*os), N*os);
hold off;
plot(f2, abs(Xos), '-o');
hold on;
grid on;
plot(f1, abs(X), '-ro');
hold off;
xlabel('Frequency (Hz)');
ylabel('Magnitude');
частотная характеристика http://www.freeimagehosting.net/uploads/e10109e535.png
обратите внимание, что в моем коде я создаю пример значения DC, отличного от нуля, с последующим резким изменением на ноль, а затем наращиванием. Затем я беру IFFT для преобразования во временную область. Затем я выполняю нулевой БПФ (который выполняется автоматически MATLAB, когда вы передаете размер БПФ больше, чем вход сигнал) на этом сигнале временной области. Обнуление во временной области приводит к интерполяции в частотной области. Используя это, мы можем видеть, как фильтр будет реагировать между образцами фильтра.
одна из самых важных вещей, котор нужно вспомнить что даже если вы устанавливаете значения реакции фильтра на, котор дали частотах путем ослаблять выходы DFT, это ничего не гарантирует для частот происходя между пунктами образца. Это означает, что чем резче ваши изменения, тем больше overshoot и колебания между образцами произойдут.
отвечая на ваш вопрос о том, как эта фильтрация должна быть выполнена. Существует несколько способов, но один из самых простых для реализации и понимания-это метод проектирования окон. Проблема с вашим текущим дизайном заключается в том, что ширина перехода огромна. Большую часть времени вы захотите как можно быстрее переходов, с как можно меньшей пульсацией.в следующем коде я создам идеальный фильтр и отобразите ответ:
N = 32;
os = 4;
Fs = 1000;
X = [ones(1,8) zeros(1,16) ones(1,8)];
x = ifftshift(ifft(X));
Xos = fft(x, N*os);
f1 = linspace(-Fs/2, Fs/2-Fs/N, N);
f2 = linspace(-Fs/2, Fs/2-Fs/(N*os), N*os);
hold off;
plot(f2, abs(Xos), '-o');
hold on;
grid on;
plot(f1, abs(X), '-ro');
hold off;
xlabel('Frequency (Hz)');
ylabel('Magnitude');
частотная характеристика http://www.freeimagehosting.net/uploads/c86f5f1700.png
обратите внимание, что существует много колебаний, вызванных резкими изменениями.
БПФ или дискретное преобразование Фурье является выборочной версией преобразования Фурье. Преобразование Фурье применяется к сигналу в непрерывном диапазоне-от бесконечности до бесконечности, в то время как DFT применяется к конечному числу выборок. Это эффект приводит к квадратному окну (усечению) во временной области при использовании DFT, поскольку мы имеем дело только с конечным числом образцов. К сожалению, DFT прямоугольной волны является функцией типа sinc(sin (x)/x).
проблема с резкими переходами в вашем фильтре (быстрый переход от 0 до 1 в одном примере) заключается в том, что это имеет очень длинный ответ во временной области, который усекается квадратным окном. Таким образом, чтобы свести к минимуму эту проблему, мы можем умножить сигнал временной области более постепенным окном. Если мы умножим окно Ханнинга, добавив строку:
x = x .* hanning(1,N).';
после принятия IFFT, мы получаем этот ответ:
частотная характеристика http://www.freeimagehosting.net/uploads/944da9dd93.png
поэтому я бы рекомендовал попытаться реализовать метод дизайна окна, поскольку он довольно прост (есть лучшие способы, но они становятся более сложными). Поскольку вы реализуете эквалайзер, я предполагаю, что вы хотите иметь возможность изменять затухания на лету, поэтому я бы предложил вычислять и хранить фильтр в частотной области всякий раз, когда происходит изменение параметров, а затем вы можете просто применить его к каждому входному звуковому буферу, взяв БПФ входного буфера, умножая на образцы фильтра частотной области, а затем выполняя ifft, чтобы вернуться во временную область. Это будет намного эффективнее, чем все ветвления, которые вы делаете для каждого образца.
во-первых, о нормализации: это известная (не) проблема. Для DFT / IDFT потребуется фактор 1 / sqrt (N) (кроме стандартных коэффициентов Косинуса / синуса) в каждом из них (прямой обратный), чтобы сделать их симметричными и действительно обратимыми. Другая возможность-разделить один из них (прямой или обратный) на N, это вопрос удобства и вкуса. Часто процедуры FFT не выполняют эту нормализацию, пользователь должен знать об этом и нормализуйте, как он предпочитает. посмотреть
во-вторых: в (скажем) 16 точка DFT, что вы называете bin 0 соответствовало бы нулевой частоте (DC),ОГРН 1 низкий freq... Бен 4 средние частоты, бин 8 к самой высокой частоте и бункеры 9...15 к "отрицательным частотам". В вашем примере, тогда,ОГРН 1 фактически и низкочастотная и средняя частота. Помимо этого соображения, ничего принципиально плохого в "уравниловки". Я не понимаю, что ты имеешь в виду!--1--> "сигнал искажается на низких частотах". Как вы это наблюдаете ?
