Двунаправленное остовное дерево

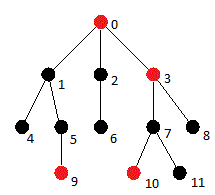
королевство имеет N городов, N-1 краев и полностью связано, поэтому наше королевство дерево (в теории графов). На этом рисунке вы можете увидеть древовидное представление вашего входного графа, в котором машины представлены красными вершинами.

кстати, вы должны рассмотреть все пути от корневой вершины до всех вершин. Таким образом, в каждом пути у вас будет несколько красных узлов, и при удалении ребер вы должны учитывать только соседние красные узлы. Например, в пути 0-10 есть две значимые пары - (0,3) и (3,10). И вы должны удалить ровно один узел (не меньше, не больше) из каждого пути, который связал вершины попарно.

Я надеюсь, что этот совет был полезным.

как говорили другие, связный граф с N вершинами и N-1 ребрами является деревом.

эта проблема требует жадного решения; я бы пошел на модификацию алгоритм Крускала:

начните с набора из N компонентов - 1 для каждого узла (города). Следите за тем, какие компоненты содержат город, занятый машиной.

Возьмите 1 край (дорога) за раз, заказ по убыванию веса (начиная с дорог, наиболее дорогостоящих для уничтожения). Для этого ребра (которое обязательно соединяет две составляющие-граф является деревом):

• если оба соседних компонента содержат город, занятый машиной, эта дорога должна быть уничтожена, отметьте ее как таковую
• в противном случае объедините соседние компоненты в один. Если один из них содержал город, занятый машиной, то и объединенный компонент тоже.

когда вы закончите со всеми ребрами, верните сумму затрат для уничтоженных дороги.

сложность будет такой же, как алгоритм Крускала, то есть почти линейной для хорошо выбранной структуры данных и метода сортировки.

pjotr имеет правильный ответ (хотя и не совсем асимптотически оптимальный), но это утверждение

эта проблема требует жадного решения

действительно требует доказательств, как и в реальном мире (в отличие от спортивного программирования), есть несколько проблем такого "рода", для которых жадное решение не является оптимальным (например, эта же проблема в общих графах, которая называется многотерминальным разрезом и является NP-жесткой). В этом случае доказательство состоит из проверки матроида аксиомы. Пусть множество ребер a ⊆ E будет независимая если граф (V, E & setminus; A) имеет точно |A| + 1 связанные компоненты, содержащие по крайней мере одну машину.

независимость пустого набора. тривиально.

наследственного имущества. пусть A-независимый набор. Каждое ребро e ∈ a соединяет две связанные компоненты графа (V, E & setminus; A) и каждая связная компонента содержит по крайней мере одну машину. При возврате e в график число связанных компонентов, содержащих по крайней мере одну машину, уменьшается на 1, поэтому ∖ {e} также независим.

свойство увеличения. пусть A и B-независимые множества с |A|

начните выполнение DFS с любого из узлов машины. Кроме того, следите за краем с минимальным весом, встречающимся до сих пор. Как только вы найдете следующий узел, который также содержит машину, удалите записанный до сих пор минимальный край. Запустите DFS с этого нового узла. Повторяйте, пока не найдете все узлы, где существуют машины.

должно быть O (N) таким образом !!

Я пишу некоторый код и вставляю все тесты.

#include <iostream>
#include<algorithm>
using namespace std;

class Line {
public:
    Line(){
        begin=0;end=0;  weight=0;
}
int begin;int end;int weight;

bool operator<(const Line& _l)const {
    return weight>_l.weight;
}
};

class Point{
public:
Point(){
    pre=0;machine=false;
}
int pre;
bool machine;
};

void DP_Matrix();
void outputLines(Line* lines,Point* points,int N);

int main() {
    DP_Matrix();
    system("pause");
    return 0;
}   

int FMSFind(Point* trees,int x){
    int r=x;
    while(trees[r].pre!=r)
        r=trees[r].pre;
    int i=x;int j;
    while(i!=r) {
            j=trees[i].pre;
        trees[i].pre=r;
        i=j;
    }
return r;
}

void DP_Matrix(){
int N,K,machine_index;scanf("%d%d",&N,&K);
Line* lines=new Line[100000];
Point* points=new Point[100000];
N--;
for(int i=0;i<N;i++) {
    scanf("%d%d%d",&lines[i].begin,&lines[i].end,&lines[i].weight);
    points[i].pre=i;
}
points[N].pre=N;
for(int i=0;i<K;i++) {
    scanf("%d",&machine_index);
    points[machine_index].machine=true;
}
long long finalRes=0;
for(int i=0;i<N;i++) {
    int bP=FMSFind(points,lines[i].begin);
    int eP=FMSFind(points,lines[i].end);
    if(points[bP].machine&&points[eP].machine){
        finalRes+=lines[i].weight;
    }
    else{
        points[bP].pre=eP;
        points[eP].machine=points[bP].machine||points[eP].machine;
        points[bP].machine=points[eP].machine;
    }
}
cout<<finalRes<<endl;
delete[] lines;
delete[] points;
}

void outputLines(Line* lines,Point* points,int N){
printf("\nLines:\n");
for(int i=0;i<N;i++){
    printf("%d\t%d\t%d\n",lines[i].begin,lines[i].end,lines[i].weight);
}
printf("\nPoints:\n");
for(int i=0;i<=N;i++){
    printf("%d\t%d\t%d\n",i,points[i].machine,points[i].pre);
}
}