Эффективная структура данных для хранения длинной последовательности (в основном последовательных) целых чисел

Другой альтернативой может быть структура данных веревки ( https://en.m.wikipedia.org/wiki/Rope_ (data_structure) ), который, кажется, поддерживает операции, которые вы просите, реализованы в O(log n) времени. В отличие от примера в Википедии, Ваш будет хранить [start,end] вместо string подпоследовательностей.

что интересно в веревке, так это ее эффективный поиск индекса в интервале. Он выполняет заказ все позиции слева на право - более низкое и высокое позиционирование (из которых ваши интервалы будут простым представлением) может быть либо вверх, либо вниз, пока движение вправо, а также полагаться на сохранение размера поддерева, который ориентирует текущее положение на основе веса слева. Поглощение частичных интервалов большими охватывающими интервалами может быть выполнено в O(log n) время путем обновления и отсоединения соответствующих сегментов дерева.

интервальные деревья, похоже, ориентированы на хранение перекрывающихся интервалов, в то время как в вашем случае это не имеет смысла. Дерево интервалов может содержать миллионы небольших перекрывающихся интервалов, которые вместе образуют лишь несколько более длинных неперекрывающихся интервалов.

Если вы хотите сохранить только неперекрывающиеся интервалы, то добавление или удаление интервала может включать в себя удаление ряда последовательных интервалов, которые попадают в новый интервал. Так быстро находя подряд интервалы и эффективное удаление потенциально большого количества интервалов имеют важное значение.

это звучит как работа для скромного связанного списка. При вставке нового интервала вы:

• поиск позиции начальной точки нового интервала.
• если он находится внутри существующего интервала, перейдите, чтобы найти положение конечной точки, расширяя существующий интервал и удаляя все интервалы, которые вы проходите по пути.
• если находится между существующими интервалами, проверьте, является ли конечная точка перед следующим существующим интервалом. Если это так, создайте новый интервал. Если конечная точка наступает после начала следующего существующего интервала, измените начальную точку следующего интервала, а затем найдите конечную точку, как описано в предыдущем абзаце.

удаление интервала будет в основном одинаковым: вы усекаете интервалы, в которых находятся начальная и конечная точки, и удаляете все интервалы между ними.

средняя и наихудшая сложность этого - N / 2 и N, где N-количество интервалов в связанном списке. Вы можете улучшить это, добавив метод, чтобы избежать итерации по всему списку, чтобы найти начальную точку; если вы знаете диапазон и распределение значений, это может быть что-то вроде хэш-таблицы; например, если значения от 1 до X и распределение однородно, вы бы сохранили таблицу длины Y, где каждый элемент указывает к интервалу, который начинается до значения X/Y. При добавлении интервала (A,B), вы должны найти таблицу[A / Y] и начать итерацию по связанному списку оттуда. Выбор значения для Y будет определяться тем, сколько пространства вы хотите использовать, по сравнению с тем, как близко вы хотите добраться до фактического положения начальной точки. Тогда сложности упадут на коэффициент Y.--2-->

(Если вы работаете на языке, где вы можете замкнуть связанный список, и просто оставить цепочку объектов, которые вы чтобы быть собранным мусором, вы можете найти местоположение начальной и конечной точек независимо, соединить их и пропустить удаление всех интервалов между ними. Я не знаю, действительно ли это увеличит скорость на практике.)

вот начало примера кода с тремя функциями диапазона, но без дальнейшей оптимизации:

function Interval(a, b, n) {
    this.start = a;
    this.end = b;
    this.next = n;
}

function IntervalList() {
    this.first = null;
}

IntervalList.prototype.addRange = function(a, b) {
    if (!this.first || b < this.first.start - 1) {
        this.first = new Interval(a, b, this.first); // insert as first element
        return;
    }
    var i = this.first;
    while (a > i.end + 1 && i.next && b >= i.next.start - 1) {
        i = i.next;                                  // locate starting point
    }
    if (a > i.end + 1) {                             // insert as new element
        i.next = new Interval(a, b, i.next);
        return;
    }
    var j = i.next;
    while (j && b >= j.start - 1) {                  // locate end point
        i.end = j.end;
        i.next = j = j.next;                         // discard overlapping interval
    }
    if (a < i.start) i.start = a;                    // update interval start
    if (b > i.end) i.end = b;                        // update interval end
}

IntervalList.prototype.delRange = function(a, b) {
    if (!this.first || b < this.first.start) return; // range before first interval
    var i = this.first;
    while (i.next && a > i.next.start) i = i.next;   // a in or after interval i
    if (a > i.start) {                               // a in interval
        if (b < i.end) {                             // range in interval -> split
            i.next = new Interval(b + 1, i.end, i.next);
            i.end = a - 1;
            return;
        }
        if (a <= i.end) i.end = a - 1;               // truncate interval
    }
    var j = a > i.start ? i.next : i;
    while (j && b >= j.end) j = j.next;              // b before or in interval j
    if (a <= this.first.start) this.first = j;       // short-circuit list
    else i.next = j;
    if (j && b >= j.start) j.start = b + 1;          // truncate interval
}

IntervalList.prototype.hasRange = function(a, b) {
    if (!this.first) return false;                   // empty list
    var i = this.first;
    while (i.next && a > i.end) i = i.next;          // a before or in interval i
    return a >= i.start && b <= i.end;               // range in interval ?
}

IntervalList.prototype.addValue = function(a) {
    this.addRange(a, a);                             // could be optimised
}

IntervalList.prototype.delValue = function(a) {
    this.delRange(a, a);                             // could be optimised
}

IntervalList.prototype.hasValue = function(a) {
    return this.hasRange(a, a);                      // could be optimised
}

IntervalList.prototype.print = function() {
    var i = this.first;
    if (i) do document.write("(" + i.start + "-" + i.end + ") "); while (i = i.next);
    document.write("<br>");
}

var intervals = new IntervalList();
intervals.addRange(100,199);
document.write("+ (100-199) &rarr; "); intervals.print();
intervals.addRange(300,399);
document.write("+ (300-399) &rarr; "); intervals.print();
intervals.addRange(200,299);
document.write("+ (200-299) &rarr; "); intervals.print();
intervals.delRange(225,275);
document.write("− (225-275) &rarr; "); intervals.print();
document.write("(150-200) ? " + intervals.hasRange(150,200) + "<br>");
document.write("(200-300) ? " + intervals.hasRange(200,300) + "<br>");

Я удивлен, что никто не предложил сегмент деревья над целочисленной областью сохраненных значений. (При использовании в геометрических приложениях, таких как графика в 2d и 3d, они называются quadtrees и octrees resp.) Вставка, удаление и поиск будут иметь сложность времени и пространства, пропорциональную количеству битов в (maxval - minval), то есть log_2 (maxval - minval), максимальные и минимальные значения целочисленной области данных.

в двух словах, мы кодируем набор целых чисел in [minval, maxval]. Узел на самом верхнем уровне 0 представляет весь этот диапазон. Узлы каждого последующего уровня представляют поддиапазоны приближенного размера (maxval-minval) / 2^k. Когда узел включен, некоторое подмножество его соответствующих значений является частью представленного набора. Когда это лист,все его значения находятся в наборе. Когда его нет, его нет.

например. если minval=0 и maxval=7, то дочерние элементы K=1 узла k=0 представляют [0..3] и [4..7]. Их дети на уровне k=2 равны [0..1][2..3][4..5] и [6..7], а узлы k=3 представляют собой отдельные элементы. Набор {[1..3], [6..7]} будет дерево (уровни слева направо):

[0..7] -- [0..3] -- [0..1]
       |         |        `-[1] 
       |         `- [2..3]
        ` [4..7]
                 `- [6..7]

нетрудно увидеть, что пространство для дерева будет O (M log (maxval - minval)), где m-количество интервалов, хранящихся в дереве.

не принято использовать деревья сегментов с динамической вставкой и удалением, но алгоритмы оказываются довольно простыми. Это требует некоторой осторожности убедитесь, что количество узлов сведено к минимуму.

вот некоторые очень легко протестированный код java.

import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;

public class SegmentTree {
  // Shouldn't differ by more than Long.MAX_VALUE to prevent overflow.
  static final long MIN_VAL = 0;
  static final long MAX_VAL = Long.MAX_VALUE;
  Node root;

  static class Node {
    Node left;
    Node right;
    Node(Node left, Node right) {
      this.left = left;
      this.right = right;
    }
  }

  private static boolean isLeaf(Node node) {
    return node != null && node.left == null && node.right == null;
  }

  private static Node reset(Node node, Node left, Node right) {
    if (node == null) {
      return new Node(left, right);
    }
    node.left = left;
    node.right = right;
    return node;
  }

  /**
   * Accept an arbitrary subtree rooted at a node representing a subset S of the range [lo,hi] and
   * transform it into a subtree representing S + [a,b]. It's assumed a >= lo and b <= hi.
   */
  private static Node add(Node node, long lo, long hi, long a, long b) {
    // If the range is empty, the interval tree is always null.
    if (lo > hi) return null;
    // If this is a leaf or insertion is outside the range, there's no change.
    if (isLeaf(node) || a > b || b < lo || a > hi) return node;
    // If insertion fills the range, return a leaf.
    if (a == lo && b == hi) return reset(node, null, null);
    // Insertion doesn't cover the range. Get the children, if any.
    Node left = null, right = null;
    if (node != null) {
      left = node.left;
      right = node.right;
    }
    // Split the range and recur to insert in halves.
    long mid = lo + (hi - lo) / 2;
    left = add(left, lo, mid, a, Math.min(b, mid));
    right = add(right, mid + 1, hi, Math.max(a, mid + 1), b);
    // Build a new node, coallescing to leaf if both children are leaves.
    return isLeaf(left) && isLeaf(right) ? reset(node, null, null) : reset(node, left, right);
  }

  /**
   * Accept an arbitrary subtree rooted at a node representing a subset S of the range [lo,hi] and
   * transform it into a subtree representing range(s) S - [a,b].  It's assumed a >= lo and b <= hi.
   */
  private static Node del(Node node, long lo, long hi, long a, long b) {
    // If the tree is null, we can't remove anything, so it's still null
    // or if the range is empty, the tree is null.
    if (node == null || lo > hi) return null;
    // If the deletion is outside the range, there's no change.
    if (a > b || b < lo || a > hi) return node; 
    // If deletion fills the range, return an empty tree.
    if (a == lo && b == hi) return null;
    // Deletion doesn't fill the range. 
    // Replace a leaf with a tree that has the deleted portion removed. 
    if (isLeaf(node)) {
      return add(add(null, lo, hi, b + 1, hi), lo, hi, lo, a - 1);
    }
    // Not a leaf. Get children, if any.
    Node left = node.left, right = node.right;
    long mid = lo + (hi - lo) / 2;
    // Recur to delete in child ranges.
    left = del(left, lo, mid, a, Math.min(b, mid));
    right = del(right, mid + 1, hi, Math.max(a, mid + 1), b);
    // Build a new node, coallescing to empty tree if both children are empty.
    return left == null && right == null ? null : reset(node, left, right);
  }

  private static class NotContainedException extends Exception {};

  private static void verifyContains(Node node, long lo, long hi, long a, long b)
      throws NotContainedException {
    // If this is a leaf or query is empty, it's always contained.
    if (isLeaf(node) || a > b) return;
    // If tree or search range is empty, the query is never contained.
    if (node == null || lo > hi) throw new NotContainedException();
    long mid = lo + (hi - lo) / 2;
    verifyContains(node.left, lo, mid, a, Math.min(b, mid));
    verifyContains(node.right, mid + 1, hi, Math.max(a, mid + 1), b);
  }

  SegmentTree addRange(long a, long b) {
    root = add(root, MIN_VAL, MAX_VAL, Math.max(a, MIN_VAL), Math.min(b, MAX_VAL));
    return this;
  }

  SegmentTree addVal(long a) {
    return addRange(a, a);
  }

  SegmentTree delRange(long a, long b) {
    root = del(root, MIN_VAL, MAX_VAL, Math.max(a, MIN_VAL), Math.min(b, MAX_VAL));
    return this;
  }

  SegmentTree delVal(long a) {
    return delRange(a, a);
  }

  boolean containsVal(long a) {
    return containsRange(a, a);
  }

  boolean containsRange(long a, long b) {
    try {
      verifyContains(root, MIN_VAL, MAX_VAL, Math.max(a, MIN_VAL), Math.min(b, MAX_VAL));
      return true;
    } catch (NotContainedException expected) {
      return false;
    }
  }

  private static final boolean PRINT_SEGS_COALESCED = true;

  /** Gather a list of possibly coalesced segments for printing. */
  private static void gatherSegs(List<Long> segs, Node node, long lo, long hi) {
    if (node == null) {
      return;
    }
    if (node.left == null && node.right == null) {
      if (PRINT_SEGS_COALESCED && !segs.isEmpty() && segs.get(segs.size() - 1) == lo - 1) {
        segs.remove(segs.size() - 1);
      } else {
        segs.add(lo);
      }
      segs.add(hi);
    } else {
      long mid = lo + (hi - lo) / 2;
      gatherSegs(segs, node.left, lo, mid);
      gatherSegs(segs, node.right, mid + 1, hi);
    }
  }

  SegmentTree print() {
    List<Long> segs = new ArrayList<>();
    gatherSegs(segs, root, MIN_VAL, MAX_VAL);
    Iterator<Long> it = segs.iterator();
    while (it.hasNext()) {
      long a = it.next();
      long b = it.next();
      System.out.print("[" + a + "," + b + "]");
    }
    System.out.println();
    return this;
  }

  public static void main(String [] args) {
    SegmentTree tree = new SegmentTree()
        .addRange(0, 4).print()
        .addRange(6, 7).print()
        .delVal(2).print()
        .addVal(5).print()
        .addRange(0,1000).print()
        .addVal(5).print()
        .delRange(22, 777).print();
    System.out.println(tree.containsRange(3, 20));
  }
}

проблема с хранением каждого интервала как пары (начало, конец) заключается в том, что если вы добавляете новый диапазон, который охватывает N ранее сохраненных интервалов, вы должны уничтожить каждый из этих интервалов, который принимает N шагов, хранятся ли интервалы в дереве, веревке или связанном списке.

(вы можете оставить их для автоматической сборки мусора, но это тоже займет время и работает только на некоторых языках.)

возможное решение для этого может быть, хранить значения (а не начальную и конечную точки интервалов) в N-арное дерево, где каждый узел представляет диапазон и хранит две N-разрядные карты, представляющие N поддиапазонов и все ли значения в этих поддиапазонах присутствуют, отсутствуют или смешаны. В случае mixed будет указатель на дочерний узел, который представляет этот диапазон rub.

пример: (использование дерева с ветвление фактора 8 и высота 2)

full range: 0-511 ; store interval 100-300

0-511:
  0- 63   64-127  128-191  192-255  256-319  320-383  384-447  448-511
   0      mixed      1        1      mixed      0        0        0

64-127:
 64- 71   72- 79   80- 87   88- 95   96-103  104-111  112-119  120-127
   0        0        0        0      mixed      1        1        1

96-103:
 96   97   98   99  100  101  102  103
  0    0    0    0    1    1    1    1

256-319:
256-263  264-271  272-279  280-287  288-295  296-303  304-311  312-319
   1        1        1        1        1      mixed      0        0

296-303:
296  297  298  299  300  301  302  303
  1    1    1    1    1    0    0    0

таким образом, дерево будет содержать эти пять узлов:

- values: 00110000, mixed: 01001000, 2 pointers to sub-nodes  
  - values: 00000111, mixed: 00001000, 1 pointer to sub-node
    - values: 00001111, mixed: 00000000
  - values: 11111000, mixed: 00000100, 1 pointer to sub-node
    - values: 11111000, mixed: 00000000

точка хранения интервала таким образом заключается в том, что вы можете отказаться от интервала без необходимости его удаления. Предположим, вы добавляете новый диапазон 200-400; в этом случае вы измените диапазон 256-319 в корневом узле с "смешанного" на "1", не удаляя или не обновляя сами узлы 256-319 и 296-303; эти узлы могут быть сохранены для последующего повторного использования (или отключены и помещены в очередь повторно используемые под-деревья или удаляются в запрограммированной сборке мусора, когда программа работает на холостом ходу или работает с нехваткой памяти).

когда вы смотрите на интервал, вам нужно только идти так глубоко вниз по дереву, как это необходимо; когда вы смотрите вверх, например, 225-275, вы обнаружите, что 192-255 все присутствует, 256-319 смешано, 256-263 и 264-271 и 272-279 все присутствуют, и вы знаете, что ответ верен. Поскольку эти значения будут храниться как растровые изображения (один для present / absent, один для mixed / solid), все значения в узле можно проверить только с помощью нескольких побитовых сравнений.

повторное использование узлов:

если узел имеет дочерний узел, и соответствующее значение позже устанавливается из mixed в all-absent или all-present, дочерний узел больше не содержит соответствующих значений (но он игнорируется). Когда значение изменяется обратно на mixed, дочерний узел можно обновить, установив все его значения на его значение в Родительском узле (до того, как он был изменен на mixed) , а затем сделав соответствующие изменения.

в приведенном выше примере, если мы добавим диапазон 0-200, это изменит дерево на:

- values: 11110000, mixed: 00001000, 2 pointers to sub-nodes  
  - (values: 00000111, mixed: 00001000, 1 pointer to sub-node)
    - (values: 00001111, mixed: 00000000)
  - values: 11111000, mixed: 00000100, 1 pointer to sub-node
    - values: 11111000, mixed: 00000000

второй и третий узлы теперь содержат устаревшие значения и игнорируются. Если мы затем удалим диапазон 80-95, значение для диапазона 64-127 в корневом узле снова изменится на смешанное, а узел для диапазона 64-127 будет повторно использован. Сначала мы устанавливаем все значения в нем на all-present (потому что это было Предыдущее значение родительского узла), а затем устанавливаем значения 80-87 88-95 и для всех-нет. Третий узел, для диапазона 96-103, остается неиспользуемым.

- values: 00110000, mixed: 01001000, 2 pointers to sub-nodes  
  - values: 11001111, mixed: 00000000, 1 pointer to sub-node
    - (values: 00001111, mixed: 00000000)
  - values: 11111000, mixed: 00000100, 1 pointer to sub-node
    - values: 11111000, mixed: 00000000

если мы затем добавили значение 100, значение для диапазона 96-103 во втором узле будет изменено на mixed снова, а третий узел будет обновлен до all-absent (его Предыдущее значение во втором узле), а затем значение 100 будет установлено в present:

- values: 00110000, mixed: 01001000, 2 pointers to sub-nodes  
  - values: 11000111, mixed: 00001000, 1 pointer to sub-node
    - values: 00001000, mixed: 00000000
  - values: 11111000, mixed: 00000100, 1 pointer to sub-node
    - values: 11111000, mixed: 00000000

сначала может показаться, что эта структура данных использует много места для хранения по сравнению с решения, которые хранят интервалы как (начало,конец) пары. Однако давайте рассмотрим (теоретический) наихудший сценарий, где каждое четное число присутствует, а каждое нечетное число отсутствует во всем 64-битном диапазоне:

Total range: 0 ~ 18,446,744,073,709,551,615  
Intervals:        9,223,372,036,854,775,808  

структура данных, которая хранит эти пары как (начало,конец), будет использовать:

Nodes:            9,223,372,036,854,775,808  
Size of node:                            16 bytes  
TOTAL:          147,573,952,589,676,412,928 bytes

если структура данных использует узлы, которые связаны через (64-битные) указатели, это добавит:

Data:           147,573,952,589,676,412,928 bytes
Pointers:        73,786,976,294,838,206,456 bytes
TOTAL:          221,360,928,884,514,619,384 bytes

N-арное дерево с ветвлением фактор 64 (и 16 для последнего уровня, чтобы получить общий диапазон 10×6 + 1×4 = 64 бита) будет использовать:

Nodes (branch):         285,942,833,483,841  
Size of branch:                         528 bytes  
Nodes (leaf):        18,014,398,509,481,984  
Size of leaf:                           144 bytes  
TOTAL:            2,745,051,201,444,873,744 bytes  

что в 53,76 раза меньше,чем (начало, конец) парных структур (или в 80,64 раза меньше, включая указатели).

расчет производился со следующим N-арным деревом:

Branch (9 levels):
value: 64-bit map
mixed: 64-bit map
sub-nodes: 64 pointers
TOTAL: 528 bytes

Leaf:
value: 64-bit map
mixed: 64-bit map
sub-nodes: 64 16-bit maps (more efficient than pointing to sub-node)
TOTAL: 144 bytes

это, конечно, наихудшее сравнение; средний случай будет очень зависеть от конкретного ввода.

вот первый пример кода я написал, чтобы проверить идею. Узлы имеют коэффициент ветвления 16, так что каждый уровень хранит 4 бита целых чисел, а общая битовая глубина может быть получена без разных листьев и ветвей. Например, создается дерево глубиной 3, представляющее диапазон 4×4 = 16 бит.

function setBits(pattern, value, mask) {                 // helper function (make inline)
    return (pattern & ~mask) | (value ? mask : 0);
}

function Node(value) { // CONSTRUCTOR
    this.value = value ? 65535 : 0;                      // set all values to 1 or 0
    this.mixed = 0;                                      // set all to non-mixed
    this.sub = null;                                     // no pointer array yet
}

Node.prototype.prepareSub = function(pos, mask, value) {
    if ((this.mixed & mask) == 0) {                      // not mixed, child possibly outdated
        var prev = (this.value & mask) >> pos;
        if (value == prev) return false;                 // child doesn't require setting
        if (!this.sub) this.sub = [];                    // create array of pointers
        if (this.sub[pos]) {
            this.sub[pos].value = prev ? 65535 : 0;      // update child node values
            this.sub[pos].mixed = 0;
        }
        else this.sub[pos] = new Node(prev);             // create new child node
    }
    return true;                                         // child requires setting
}

Node.prototype.set = function(value, a, b, step) {
    var posA = Math.floor(a / step), posB = Math.floor(b / step);
    var maskA = 1 << posA, maskB = 1 << posB;
    a %= step; b %= step;

    if (step == 1) {                                     // node is leaf
        var vMask = (maskB | (maskB - 1)) ^ (maskA - 1); // bits posA to posB inclusive
        this.value = setBits(this.value, value, vMask);
    }
    else if (posA == posB) {                             // only 1 sub-range to be set
        if (a == 0 && b == step - 1)                     // a-b is full sub-range
        {
            this.value = setBits(this.value, value, maskA);
            this.mixed = setBits(this.mixed, 0, maskA);
        }
        else if (this.prepareSub(posA, maskA, value)) {  // child node requires setting
            var solid = this.sub[posA].set(value, a, b, step >> 4);     // recurse
            this.value = setBits(this.value, solid ? value : 0, maskA); // set value
            this.mixed = setBits(this.mixed, solid ? 0 : 1, maskA);     // set mixed
        }
    }
    else {                                               // multiple sub-ranges to set
        var vMask = (maskB - 1) ^ (maskA | (maskA - 1)); // bits between posA and posB
        this.value = setBits(this.value, value, vMask);  // set inbetween values
        this.mixed &= ~vMask;                            // set inbetween to solid
        var solidA = true, solidB = true;
        if (a != 0 && this.prepareSub(posA, maskA, value)) {          // child needs setting
            solidA = this.sub[posA].set(value, a, step - 1, step >> 4);
        }
        if (b != step - 1 && this.prepareSub(posB, maskB, value)) {   // child needs setting
            solidB = this.sub[posB].set(value, 0, b, step >> 4);
        }
        this.value = setBits(this.value, solidA ? value : 0, maskA);  // set value
        this.value = setBits(this.value, solidB ? value : 0, maskB);
        if (solidA) this.mixed &= ~maskA; else this.mixed |= maskA;   // set mixed
        if (solidB) this.mixed &= ~maskB; else this.mixed |= maskB;
    }
    return this.mixed == 0 && this.value == 0 || this.value == 65535; // solid or mixed
}

Node.prototype.check = function(a, b, step) {
    var posA = Math.floor(a / step), posB = Math.floor(b / step);
    var maskA = 1 << posA, maskB = 1 << posB;
    a %= step; b %= step;
    var vMask = (maskB - 1) ^ (maskA | (maskA - 1));     // bits between posA and posB

    if (step == 1) {
        vMask = posA == posB ? maskA : vMask | maskA | maskB;
        return (this.value & vMask) == vMask;
    }
    if (posA == posB) {
        var present = (this.mixed & maskA) ? this.sub[posA].check(a, b, step >> 4) : this.value & maskA;
        return !!present;
    }
    var present = (this.mixed & maskA) ? this.sub[posA].check(a, step - 1, step >> 4) : this.value & maskA;
    if (!present) return false;
    present = (this.mixed & maskB) ? this.sub[posB].check(0, b, step >> 4) : this.value & maskB;
    if (!present) return false;
    return (this.value & vMask) == vMask;
}

function NaryTree(factor, depth) { // CONSTRUCTOR
    this.root = new Node();
    this.step = Math.pow(factor, depth);
}

NaryTree.prototype.addRange = function(a, b) {
    this.root.set(1, a, b, this.step);
}

NaryTree.prototype.delRange = function(a, b) {
    this.root.set(0, a, b, this.step);
}

NaryTree.prototype.hasRange = function(a, b) {
    return this.root.check(a, b, this.step);
}

var intervals = new NaryTree(16, 3);                  // create tree for 16-bit range

// CREATE RANDOM DATA AND RUN TEST
document.write("Created N-ary tree for 16-bit range.<br>Randomly adding/deleting 100000 intervals...");
for (var test = 0; test < 100000; test++) {
    var a = Math.floor(Math.random() * 61440);
    var b = a + Math.floor(Math.random() * 4096);
    if (Math.random() > 0.5) intervals.addRange(a,b);
    else intervals.delRange(a,b);
}
document.write("<br>Checking a few random intervals:<br>");
for (var test = 0; test < 8; test++) {
    var a = Math.floor(Math.random() * 65280);
    var b = a + Math.floor(Math.random() * 256);
    document.write("Tree has interval " + a + "-" + b + " ? " + intervals.hasRange(a,b),".<br>");
}

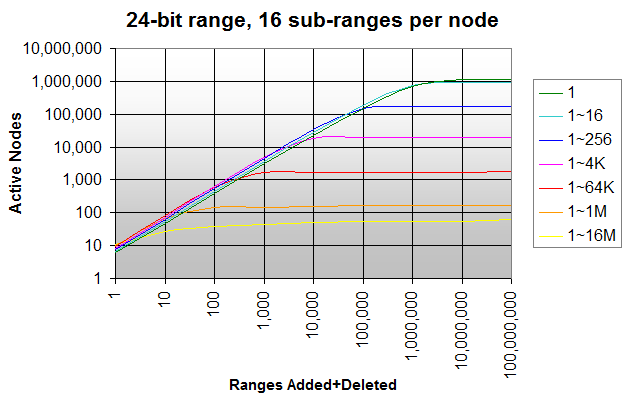
я провел тест, чтобы проверить, сколько узлов создается, и сколько из них являются активными или бездействующими. Я использовал общий диапазон 24-бит (так что Я мог бы протестировать худший случай, не исчерпывая памяти), разделенный на 6 уровней по 4 бита (поэтому каждый узел имеет 16 поддиапазонов); количество узлов, которые необходимо проверить или обновить при добавлении, удалении или проверке интервала, составляет 11 или меньше. Максимальное количество узлов в этой схеме-1,118,481.

на приведенном ниже графике показано количество активных узлов при добавлении / удалении случайных интервалов с диапазоном 1 (целые числа), 1~16, 1~256 ... 1~16M (полный диапасон).

добавление и удаление целых чисел (темно-зеленая линия) создает активные узлы, близкие к максимальным 1,118,481 узлам, при этом почти никакие узлы не бездействуют. Максимум достигается после добавления и удаления около 16M целых чисел (=количество целых чисел в диапазоне).

если вы добавляете и удаляете случайные интервалы в большем диапазоне, количество созданных узлов примерно одинаково, но больше из них дремлет. Если вы добавляете случайные интервалы в полном диапазоне 1~16M (ярко-желтая линия), менее 64 узлов активны в любое время, независимо от того, сколько интервалов вы продолжаете добавлять или удалять.

это уже дает представление о том, где эта структура данных может быть полезна в отличие от других: чем больше узлов бездействуют, тем больше интервалов/узлов необходимо будет удалить в других схемах.

С другой стороны, он показывает, как эта структура данных может быть слишком мало места-неэффективно для определенных диапазонов, типов и объемов ввода. Вы можете ввести систему утилизации бездействующих узлов, но это отнимает преимущество того, что бездействующие узлы немедленно повторно используются.

много места в дереве N-ary занимают указатели на дочерние узлы. Если полный диапазон достаточно мал, вы можете сохранить дерево в массиве. Для 32-разрядного диапазона, который займет 580 МБ (546 МБ для растровых изображений "значение" и 34 МБ для "смешанных" растровых изображений). Это более эффективно для пространства, потому что вы храните только растровые изображения, и вам не нужны указатели на дочерние узлы, потому что все имеет фиксированное место в массиве. У вас будет преимущество дерева с глубиной 7, поэтому любая операция может быть выполнена путем проверки 15 "узлов" или меньше, и никакие узлы не должны быть созданы или удалены во время операций добавления/удаления/проверки.

вот пример кода, который я использовал, чтобы попробовать идею N-ary-tree-in-an-array; он использует 580MB для хранения дерева N-ary с ветвлением фактор 16 и глубина 7, для 32-битного диапазона (к сожалению, диапазон выше 40 бит или около того, вероятно, за пределами возможностей памяти любого нормального компьютера). В дополнение к запрошенным функциям он также может проверить, полностью ли отсутствует интервал, используя notValue () и notRange ().

#include <iostream>

inline uint16_t setBits(uint16_t pattern, uint16_t mask, uint16_t value) {
    return (pattern & ~mask) | (value & mask);
}

class NaryTree32 {
    uint16_t value[0x11111111], mixed[0x01111111];

    bool set(uint32_t a, uint32_t b, uint16_t value = 0xFFFF, uint8_t bits = 28, uint32_t offset = 0) {
        uint8_t posA = a >> bits, posB = b >> bits;
        uint16_t maskA = 1 << posA, maskB = 1 << posB;
        uint16_t mask = maskB ^ (maskA - 1) ^ (maskB - 1);

        // IF NODE IS LEAF: SET VALUE BITS AND RETURN WHETHER VALUES ARE MIXED
        if (bits == 0) {
            this->value[offset] = setBits(this->value[offset], mask, value);
            return this->value[offset] != 0 && this->value[offset] != 0xFFFF;
        }

        uint32_t offsetA = offset * 16 + posA + 1, offsetB = offset * 16 + posB + 1;
        uint32_t subMask = ~(0xFFFFFFFF << bits);
        a &= subMask; b &= subMask;

        // IF SUB-RANGE A IS MIXED OR HAS WRONG VALUE
        if (((this->mixed[offset] & maskA) != 0 || (this->value[offset] & maskA) != (value & maskA))
        && (a != 0 || posA == posB && b != subMask)) {

            // IF SUB-RANGE WAS PREVIOUSLY SOLID: UPDATE TO PREVIOUS VALUE
            if ((this->mixed[offset] & maskA) == 0) {
                this->value[offsetA] = (this->value[offset] & maskA) ? 0xFFFF : 0x0000;
                if (bits != 4) this->mixed[offsetA] = 0x0000;
            }
            // RECURSE AND IF SUB-NODE IS MIXED: SET MIXED BIT AND REMOVE A FROM MASK
            if (this->set(a, posA == posB ? b : subMask, value, bits - 4, offsetA)) {
                this->mixed[offset] |= maskA;
                mask ^= maskA;
            }
        }
        // IF SUB-RANGE B IS MIXED OR HAS WRONG VALUE
        if (((this->mixed[offset] & maskB) != 0 || (this->value[offset] & maskB) != (value & maskB))
        && b != subMask && posA != posB) {

            // IF SUB-RANGE WAS PREVIOUSLY SOLID: UPDATE SUB-NODE TO PREVIOUS VALUE
            if ((this->mixed[offset] & maskB) == 0) {
                this->value[offsetB] = (this->value[offset] & maskB) ? 0xFFFF : 0x0000;
                if (bits > 4) this->mixed[offsetB] = 0x0000;
            }
            // RECURSE AND IF SUB-NODE IS MIXED: SET MIXED BIT AND REMOVE A FROM MASK
            if (this->set(0, b, value, bits - 4, offsetB)) {
                this->mixed[offset] |= maskB;
                mask ^= maskB;
            }
        }
        // SET VALUE AND MIXED BITS THAT HAVEN'T BEEN SET YET AND RETURN WHETHER NODE IS MIXED
        if (mask) {
            this->value[offset] = setBits(this->value[offset], mask, value);
            this->mixed[offset] &= ~mask;
        }
        return this->mixed[offset] != 0 || this->value[offset] != 0 && this->value[offset] != 0xFFFF;
    }

    bool check(uint32_t a, uint32_t b, uint16_t value = 0xFFFF, uint8_t bits = 28, uint32_t offset = 0) {
        uint8_t posA = a >> bits, posB = b >> bits;
        uint16_t maskA = 1 << posA, maskB = 1 << posB;
        uint16_t mask = maskB ^ (maskA - 1) ^ (maskB - 1);

        // IF NODE IS LEAF: CHECK BITS A TO B INCLUSIVE AND RETURN
        if (bits == 0) {
            return (this->value[offset] & mask) == (value & mask);
        }

        uint32_t subMask = ~(0xFFFFFFFF << bits);
        a &= subMask; b &= subMask;

        // IF SUB-RANGE A IS MIXED AND PART OF IT NEEDS CHECKING: RECURSE AND RETURN IF FALSE
        if ((this->mixed[offset] & maskA) && (a != 0 || posA == posB && b != subMask)) {
            if (this->check(a, posA == posB ? b : subMask, value, bits - 4, offset * 16 + posA + 1)) {
                mask ^= maskA;
            }
            else return false;
        }
        // IF SUB-RANGE B IS MIXED AND PART OF IT NEEDS CHECKING: RECURSE AND RETURN IF FALSE
        if (posA != posB && (this->mixed[offset] & maskB) && b != subMask) {
            if (this->check(0, b, value, bits - 4, offset * 16 + posB + 1)) {
                mask ^= maskB;
            }
            else return false;
        }
        // CHECK INBETWEEN BITS (AND A AND/OR B IF NOT YET CHECKED) WHETHER SOLID AND CORRECT
        return (this->mixed[offset] & mask) == 0 && (this->value[offset] & mask) == (value & mask);
    }

    public:

    NaryTree32() { // CONSTRUCTOR: INITIALISES ROOT NODE
        this->value[0] = 0x0000;
        this->mixed[0] = 0x0000;
    }

    void addValue(uint32_t a)             {this->set(a, a);}
    void addRange(uint32_t a, uint32_t b) {this->set(a, b);}
    void delValue(uint32_t a)             {this->set(a, a, 0);}
    void delRange(uint32_t a, uint32_t b) {this->set(a, b, 0);}
    bool hasValue(uint32_t a)             {return this->check(a, a);}
    bool hasRange(uint32_t a, uint32_t b) {return this->check(a, b);}
    bool notValue(uint32_t a)             {return this->check(a, a, 0);}
    bool notRange(uint32_t a, uint32_t b) {return this->check(a, b, 0);}
};

int main() {
    NaryTree32 *tree = new NaryTree32();

    tree->addRange(4294967280, 4294967295);
    std::cout << tree->hasRange(4294967280, 4294967295) << "\n";
    tree->delValue(4294967290);
    std::cout << tree->hasRange(4294967280, 4294967295) << "\n";
    tree->addRange(1000000000, 4294967295);
    std::cout << tree->hasRange(4294967280, 4294967295) << "\n";
    tree->delRange(2000000000, 4294967280);
    std::cout << tree->hasRange(4294967280, 4294967295) << "\n";

    return 0;
}