Экстракт контуры из ContourPlot в Mathematica
У меня есть функция f(x,y) двух переменных, из которых мне нужно знать расположение кривых, при которых она пересекает ноль. ContourPlot делает это очень эффективно (то есть: он использует умные многосеточные методы, а не просто грубое сканирование), но просто дает мне сюжет. Я хотел бы иметь набор значений {x,y} (с некоторым заданным разрешением) или, возможно, некоторую интерполирующую функцию, которая позволяет мне получить доступ к местоположению этих контуров.
есть мысли извлечение этого из полной формы ContourPlot, но это, кажется, немного взломать. Есть лучший способ сделать это?
2 ответов
если вы в конечном итоге извлечения точек из ContourPlot, это один простой способ сделать это:
points = Cases[
Normal@ContourPlot[Sin[x] Sin[y] == 1/2, {x, -3, 3}, {y, -3, 3}],
Line[pts_] -> pts,
Infinity
]
Join @@ points (* if you don't want disjoint components to be separate *)
редактировать
получается, что ContourPlot не производит очень точные контуры. Они, конечно, предназначены для построения графиков и достаточно хороши для этого, но точки не лежат точно на контурах:
In[78]:= Take[Join @@ points /. {x_, y_} -> Sin[x] Sin[y] - 1/2, 10]
Out[78]= {0.000163608, 0.0000781187, 0.000522698, 0.000516078,
0.000282781, 0.000659909, 0.000626086, 0.0000917416, 0.000470424,
0.0000545409}
мы можем попытаться придумать наш собственный метод, чтобы проследить контур, но это много проблем, чтобы сделать это в общем виде. Вот концепция, которая работает для плавно меняющихся функций, имеющих плавные контуры:
начните с некоторой точки (
pt0), и найти пересечение с контуром по градиентуf.теперь у нас есть точка на контуре. Перемещение по касательной контура фиксированным шагом (
resolution), затем повторите с шага 1.
вот базовая реализация, которая работает только с функциями это можно дифференцировать символически:
rot90[{x_, y_}] := {y, -x}
step[f_, pt : {x_, y_}, pt0 : {x0_, y0_}, resolution_] :=
Module[
{grad, grad0, t, contourPoint},
grad = D[f, {pt}];
grad0 = grad /. Thread[pt -> pt0];
contourPoint =
grad0 t + pt0 /. First@FindRoot[f /. Thread[pt -> grad0 t + pt0], {t, 0}];
Sow[contourPoint];
grad = grad /. Thread[pt -> contourPoint];
contourPoint + rot90[grad] resolution
]
result = Reap[
NestList[step[Sin[x] Sin[y] - 1/2, {x, y}, #, .5] &, {1, 1}, 20]
];
ListPlot[{result[[1]], result[[-1, 1]]}, PlotStyle -> {Red, Black},
Joined -> True, AspectRatio -> Automatic, PlotMarkers -> Automatic]
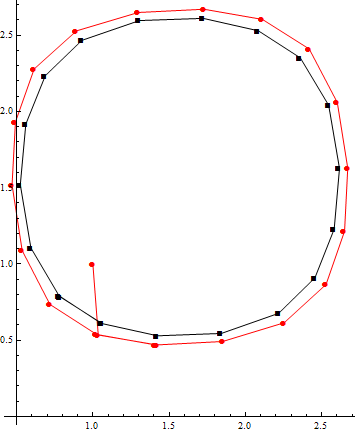
красные точки являются "начальными точками", в то время как черные точки являются трассировкой контура.
Изменить 2
возможно, это более простое и лучшее решение использовать подобную технику, чтобы сделать точки, которые мы получаем от ContourPlot более точное. Начните с начальной точки, затем двигайтесь вдоль градиента, пока мы не пересечем контур.
отметьте, что эта реализация также будет работать с функциями, которые не могут быть дифференцированы символически. Просто определите функцию как f[x_?NumericQ, y_?NumericQ] := ... если это так.
f[x_, y_] := Sin[x] Sin[y] - 1/2
refine[f_, pt0 : {x_, y_}] :=
Module[{grad, t},
grad = N[{Derivative[1, 0][f][x, y], Derivative[0, 1][f][x, y]}];
pt0 + grad*t /. FindRoot[f @@ (pt0 + grad*t), {t, 0}]
]
points = Join @@ Cases[
Normal@ContourPlot[f[x, y] == 0, {x, -3, 3}, {y, -3, 3}],
Line[pts_] -> pts,
Infinity
]
refine[f, #] & /@ points
небольшое изменение для извлечения точек из ContourPlot (возможно, из-за Дэвида парк):
pts = Cases[
ContourPlot[Cos[x] + Cos[y] == 1/2, {x, 0, 4 Pi}, {y, 0, 4 Pi}],
x_GraphicsComplex :> First@x, Infinity];
или (как список {x, y} точек)
ptsXY = Cases[
Cases[ContourPlot[
Cos[x] + Cos[y] == 1/2, {x, 0, 4 Pi}, {y, 0, 4 Pi}],
x_GraphicsComplex :> First@x, Infinity], {x_, y_}, Infinity];
редактировать
как обсуждалось здесь, an статьи Пол Эббот в Журнал Mathematica (поиск корней в интервале) дает следующие два альтернативных метода для получения списка значений {x, y} из ContourPlot, в том числе (!)
ContourPlot[...][[1, 1]]
для приведенного выше примера
ptsXY2 = ContourPlot[
Cos[x] + Cos[y] == 1/2, {x, 0, 4 Pi}, {y, 0, 4 Pi}][[1, 1]];
и
ptsXY3 = Cases[
Normal@ContourPlot[
Cos[x] + Cos[y] == 1/2, {x, 0, 4 Pi}, {y, 0, 4 Pi}],
Line[{x__}] :> x, Infinity];
здесь
ptsXY2 == ptsXY == ptsXY3
