Эллипс участок библиотек matplotlib.pyplot (Python)

демонстрация эллипса matplotlib хороша. Но я не мог реализовать его в своем коде без цикла for. Я получал ошибку осей. Вот что я сделал вместо этого, где, конечно, центр xy-это мои собственные координаты с соответствующей шириной и высотой, основанные на изображении, над которым я построил эллипс.

from matplotlib.patches import Ellipse

plt.figure()
ax = plt.gca()

ellipse = Ellipse(xy=(157.18, 68.4705), width=0.036, height=0.012, 
                        edgecolor='r', fc='None', lw=2)
ax.add_patch(ellipse)

этот код частично основан на самом первом поле кода на на этой странице. См. ответ Криса выше для ссылки на matplotlib.patches.Ellipse.

Если вы не хотите использовать патч, вы можете использовать параметрическое уравнение эллипса : x = u+a.cos (t) ; y = v+b.sin (t)

import numpy as np
from matplotlib import pyplot as plt
from math import pi

u=1.     #x-position of the center
v=0.5    #y-position of the center
a=2.     #radius on the x-axis
b=1.5    #radius on the y-axis

t = np.linspace(0, 2*pi, 100)
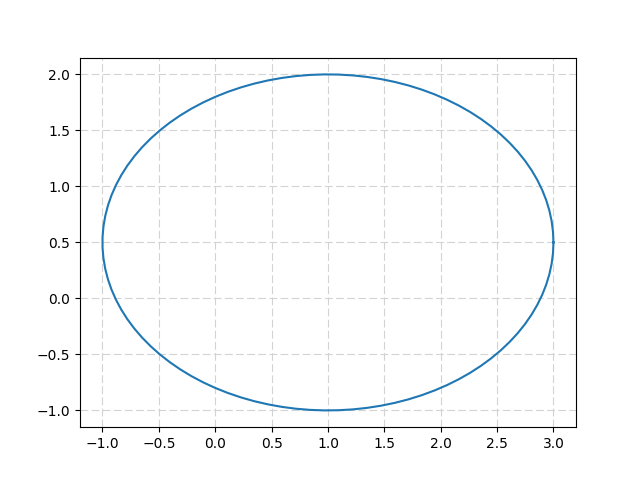
plt.plot( u+a*np.cos(t) , v+b*np.sin(t) )
plt.grid(color='lightgray',linestyle='--')
plt.show()

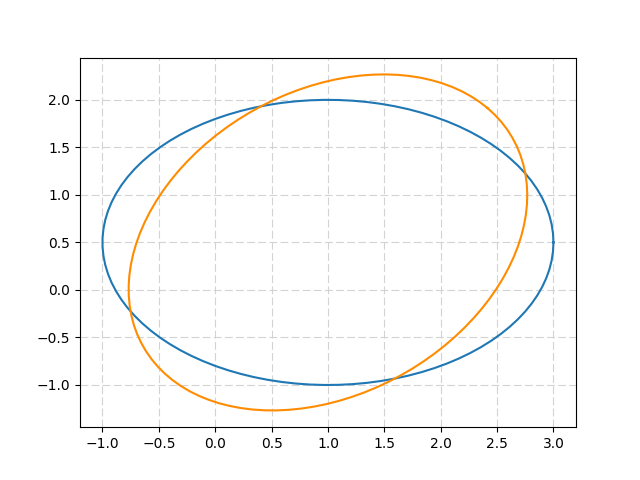
что дает : Эллипс можно вращать благодаря матрице 2D-вращения:

import numpy as np
from matplotlib import pyplot as plt
from math import pi, cos, sin

u=1.       #x-position of the center
v=0.5      #y-position of the center
a=2.       #radius on the x-axis
b=1.5      #radius on the y-axis
t_rot=pi/4 #rotation angle

t = np.linspace(0, 2*pi, 100)
Ell = np.array([a*np.cos(t) , b*np.sin(t)])  
     #u,v removed to keep the same center location
R_rot = np.array([[cos(t_rot) , -sin(t_rot)],[sin(t_rot) , cos(t_rot)]])  
     #2-D rotation matrix

Ell_rot = np.zeros((2,Ell.shape[1]))
for i in range(Ell.shape[1]):
    Ell_rot[:,i] = np.dot(R_rot,Ell[:,i])

plt.plot( u+Ell[0,:] , v+Ell[1,:] )     #initial ellipse
plt.plot( u+Ell_rot[0,:] , v+Ell_rot[1,:],'darkorange' )    #rotated ellipse
plt.grid(color='lightgray',linestyle='--')
plt.show()

возвращает :