Эллипс вокруг данных в MATLAB

Я хотел бы воспроизвести следующий рисунок в MATLAB:

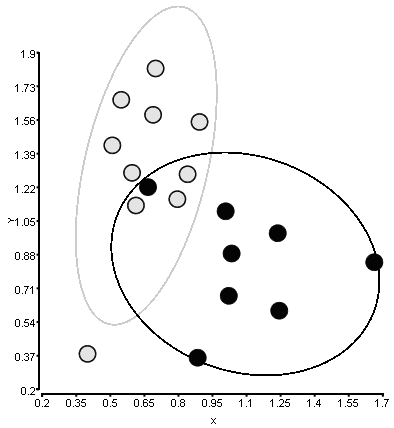
exampleee.png

существует два класса точек с координатами X и Y. Я хотел бы окружить каждый класс эллипсом с одним параметром стандартного отклонения, который определяет, как далеко эллипс будет идти вдоль оси.

фигура была создана с помощью другого программного обеспечения, и я точно не понимаю, как он вычисляет эллипс.

вот данные, которые я использую для этого фигура. 1-й столбец-класс, 2-й-X, 3-й-Y. Я могу использовать gscatter нарисовать себе очки.

A = [
    0   0.89287 1.54987
    0   0.69933 1.81970
    0   0.84022 1.28598
    0   0.79523 1.16012
    0   0.61266 1.12835
    0   0.39950 0.37942
    0   0.54807 1.66173
    0   0.50882 1.43175
    0   0.68840 1.58589
    0   0.59572 1.29311
    1   1.00787 1.09905
    1   1.23724 0.98834
    1   1.02175 0.67245
    1   0.88458 0.36003
    1   0.66582 1.22097
    1   1.24408 0.59735
    1   1.03421 0.88595
    1   1.66279 0.84183
];

gscatter(A(:,2),A(:,3),A(:,1))

кстати, здесь именно поэтому вопрос о том, как рисовать эллипс. Итак, нам просто нужно знать все параметры, чтобы нарисовать его.

обновление:

Я согласен с тем, что центр можно вычислить как средство координат X и Y. Вероятно, мне придется использовать анализ основных компонентов (PRINCOMP) для каждого класса определить угол и форма. Все еще думаю...

15
ellipse matlab normal-distribution plot standard-deviation

3 ответов

рассмотрим код:

%# generate data
num = 50;
X = [ mvnrnd([0.5 1.5], [0.025 0.03 ; 0.03 0.16], num) ; ...
      mvnrnd([1 1], [0.09 -0.01 ; -0.01 0.08], num)   ];
G = [1*ones(num,1) ; 2*ones(num,1)];

gscatter(X(:,1), X(:,2), G)
axis equal, hold on

for k=1:2
    %# indices of points in this group
    idx = ( G == k );

    %# substract mean
    Mu = mean( X(idx,:) );
    X0 = bsxfun(@minus, X(idx,:), Mu);

    %# eigen decomposition [sorted by eigen values]
    [V D] = eig( X0'*X0 ./ (sum(idx)-1) );     %#' cov(X0)
    [D order] = sort(diag(D), 'descend');
    D = diag(D);
    V = V(:, order);

    t = linspace(0,2*pi,100);
    e = [cos(t) ; sin(t)];        %# unit circle
    VV = V*sqrt(D);               %# scale eigenvectors
    e = bsxfun(@plus, VV*e, Mu'); %#' project circle back to orig space

    %# plot cov and major/minor axes
    plot(e(1,:), e(2,:), 'Color','k');
    %#quiver(Mu(1),Mu(2), VV(1,1),VV(2,1), 'Color','k')
    %#quiver(Mu(1),Mu(2), VV(1,2),VV(2,2), 'Color','k')
end

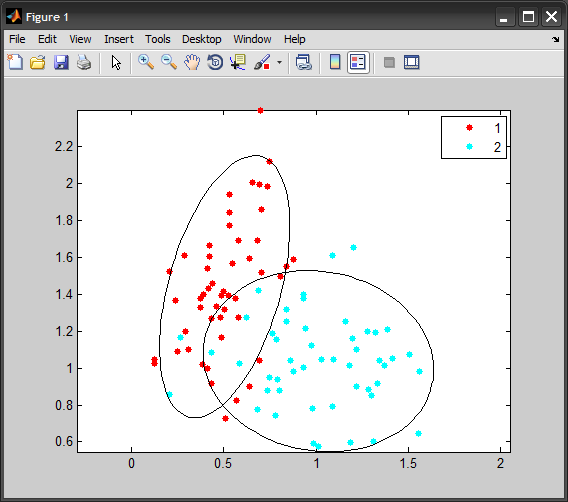
screenshot

редактировать

Если вы хотите, чтобы эллипс представлял определенный уровень стандартного отклонения, правильный способ сделать это путем масштабирования ковариационной матрицы:

STD = 2;                     %# 2 standard deviations
conf = 2*normcdf(STD)-1;     %# covers around 95% of population
scale = chi2inv(conf,2);     %# inverse chi-squared with dof=#dimensions

Cov = cov(X0) * scale;
[V D] = eig(Cov);

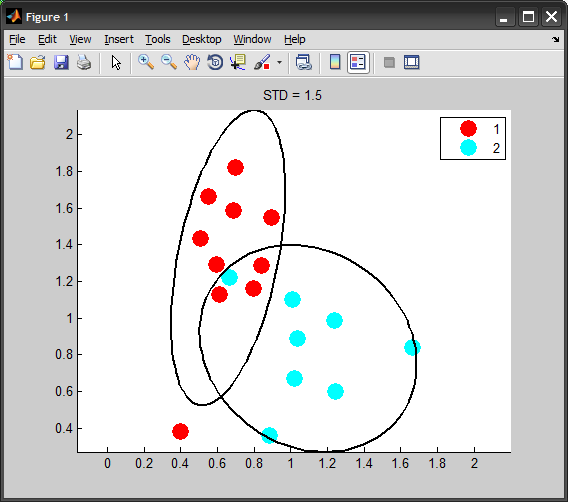
OP_DATA

17

Я бы попробовал следующий подход:

  1. вычислить центроид x-y для центра эллипса (x,y в связан вопрос)
  2. вычислить линию линейной регрессии, чтобы получить ориентацию главной оси эллипса (угол)
  3. вычислить стандартное отклонение по осям x и y
  4. перевести стандартные отклонения x-y, чтобы они были ортогональны линии подгонки (a,b)
2

я предположу, что в одной матрице есть только один набор точек, например

B = A(1:10,2:3);

эту процедуру можно воспроизвести для каждого набора данных.

  1. вычислить центр эллипсоида, который является средним из точек. Функция Матлаб: mean
  2. центр данных. Функция Матлаб bsxfun
  3. вычислить главную ось эллипсоида и их соответствующую величину. Функция Matlab: eig

последовательные шаги проиллюстрированы ниже:

Center = mean(B,1);
Centered_data = bsxfun(@minus,B,Center);
[AX,MAG] = eig(Centered_data' * Centered_data);

столбцы AX содержат векторы, описывающие главную ось эллипсоида, а диагональ MAG содержит информацию об их величине. Чтобы построить эллипсоид, масштабируйте каждую главную ось квадратным корнем ее величины.

надеюсь, что это помогает.

А.

1