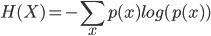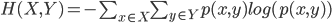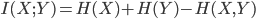Энтропия Шеннона к взаимной информации
у меня есть статистика по некоторым свойствам, таким как:
1st iter : p1:10 p2:0 p3:12 p4:33 p5:0.17 p6:ok p8:133 p9:89
2nd iter : p1:43 p2:1 p6:ok p8:12 p9:33
3rd iter : p1:14 p2:0 p3:33 p5:0.13 p9:2
...
(p1 -> number of tries, p2 -> try done well, p3..pN -> properties of try).
мне нужно рассчитать количество информации о каждом свойстве. После некоторых процедур квантования (например. до 10 уровней), чтобы сделать все входные номера на одном уровне входной файл начинает выглядеть так:
p0: 4 3 2 4 5 5 6 7
p3: 4 5 3 3
p4: 5 3 3 2 1 2 3
...
здесь p(0) = funct(p1,p2).
не каждая строка ввода получила каждый pK так len(pk) <= len(p0).
теперь я знаю, как вычислить энтропию каждого свойства через Шеннон энтропия для каждой линии. Мне нужно рассчитать взаимную информацию отсюда.
расчет совместной энтропии для взаимной информации I(p0,pK) застрял из-за разной длины.
я вычисляю энтропию для одного такого элемента:
def entropy(x):
probs = [np.mean(x == c) for c in set(x)]
return np.sum(-p * np.log2(p) for p in probs)
Итак, для сустава мне нужно использовать product для генерации входного массива x и использовать zip(p0,pk) вместо set(x)?
2 ответов
я предполагаю, что вы хотите, чтобы вычислить взаимную информацию между p1 и каждый из p2, p3,... впоследствии.
1) Расчет H(X) как энтропия из p1 с:
каждого x будучи последующим элементом из p1.
2) Расчет H(Y) как энтропия от pK С тем же уравнением, с каждым x будучи последующим элементом из p1
3) создать новую пару коллекция из p1 и pK:
pairs = zip(p1, pK)
обратите внимание, что если значения в Столбцах ваших данных имеют другое значение, то вы, вероятно, должны заполнить недостающие данные (например, используя 0s или значения из предыдущей итерации).
4) вычислить совместную энтропию H(X,Y) использование:
обратите внимание, что вы не можете просто использовать первое уравнение и рассматривать каждую пару как один элемент - вы должны перебирать все Декартово произведение между p1 и pK в этом уравнении вычисление вероятностей с использованием pairs коллекция. Итак, для итерации по всему декартову продукту используйте for xy in itertools.product(p1, pK): ....
5), то вы можете иметь взаимную информацию между p1 и pK as:
используя возможности numpy, вы можете рассчитать совместную энтропию, как представлено здесь:
def entropy(X, Y):
probs = []
for c1 in set(X):
for c2 in set(Y):
probs.append(np.mean(np.logical_and(X == c1, Y == c2)))
return np.sum(-p * np.log2(p) for p in probs if p > 0)
здесь if p > 0 согласуется с определение энтропии:
в случае p (xя) = 0 для некоторого i значение соответствующего слагаемого 0 logb(0) принимается равным 0
если вы не хотите использовать numpy, то версия без него может выглядеть примерно так:
def entropyPart(p):
if not p:
return 0
return -p * math.log(p)
def entropy(X, Y):
pairs = zip(X, Y)
probs = []
for pair in itertools.product(X,Y):
probs.append(1.0 * sum([p == pair for p in pairs]) / len(pairs))
return sum([entropyPart(p) for p in probs])
возьмите формулу из раздела формального определения этой статья в Википедии. Они называют это информационной выгодой, но это то же самое, что и взаимная информация. Чтобы вычислить энтропию образца, содержащегося в этой формуле, возьмите формулу из раздела определения этой статья в Википедии.
Итак, вы сначала вычисляете энтропию всего набора данных и вычитаете из нее энтропию, которая остается, когда вы знаете значение атрибута в вопросе.
многомерная гистограмма может быть рассчитана в Python с помощью numpy.histogramdd().