Есть ли способ построить Line2D в координатах точек в Matplotlib в Python?
это очень прямо вперед, чтобы построить линию между двумя точками (x1, y1) и (x2, y2) на Matplotlib используя Line2D:
Line2D(xdata=(x1, x2), ydata=(y1, y2))
но в моем конкретном случае я должен рисовать экземпляры Line2D, используя координаты точек поверх регулярных графиков, которые все используют координаты данных. Это возможно?
2 ответов
как упоминал @tom, ключ-это transform kwarg. Если вы хотите, чтобы данные исполнителя интерпретировались как находящиеся в координатах "пиксель", укажите transform=IdentityTransform().
С Помощью Преобразования
преобразования являются ключевым понятием в matplotlib. Преобразование принимает координаты, в которых находятся данные исполнителя, и преобразует их для отображения координат-другими словами, пикселей на экране.
если вы еще не видели его, дайте библиотек matplotlib трансформирует учебник быстрое чтение. Я собираюсь предположить мимолетное знакомство с первыми несколькими абзацами этого урока, поэтому, если вы
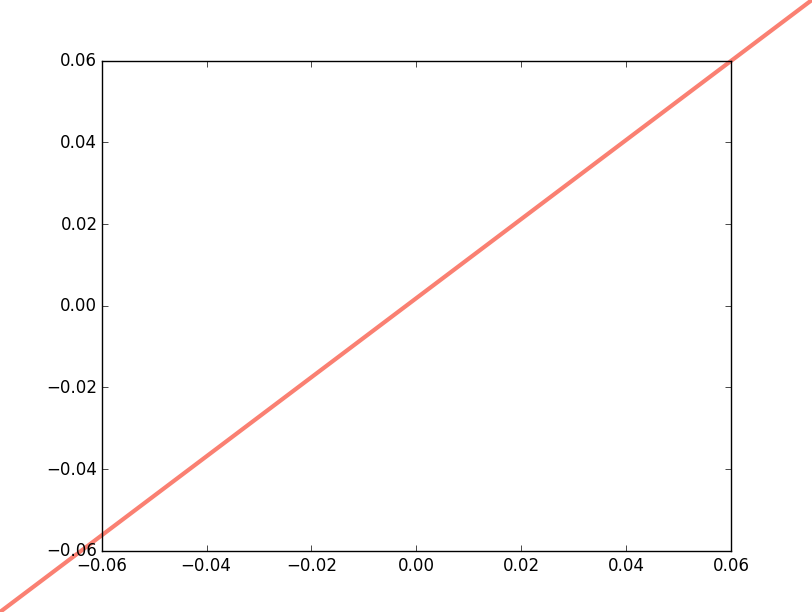
например, если мы хотим провести линию по всей фигуре, мы бы использовали что-то вроде:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
# The "clip_on" here specifies that we _don't_ want to clip the line
# to the extent of the axes
ax.plot([0, 1], [0, 1], lw=3, color='salmon', clip_on=False,
transform=fig.transFigure)
plt.show()
эта строка всегда протяните от нижнего левого угла фигуры до верхнего правого угла, независимо от того, как мы интерактивно изменение размера/масштабирование / панорамирование участка.
рисунок в пикселях
наиболее общие преобразования вы будете использовать ax.transData, ax.transAxes и fig.transFigure. Однако, чтобы рисовать точки / пиксели, вы на самом деле не хотите никакого преобразования вообще. В этом случае вы создадите новый экземпляр преобразования, который ничего не делает:IdentityTransform. Это указывает, что данные для исполнителя находятся в "необработанных" пикселях.
в любое время, когда вы хотите построить в пикселях" raw", укажите transform=IdentityTransform() для художник.
если вы хотите работать в точках, вспомните, что есть 72 точки на дюйм, и что для matplotlib,fig.dpi управляет количеством пикселей в "дюйме" (он фактически не зависит от физического дисплея). Поэтому мы можем преобразовать точки в пиксели с помощью простой формулы.
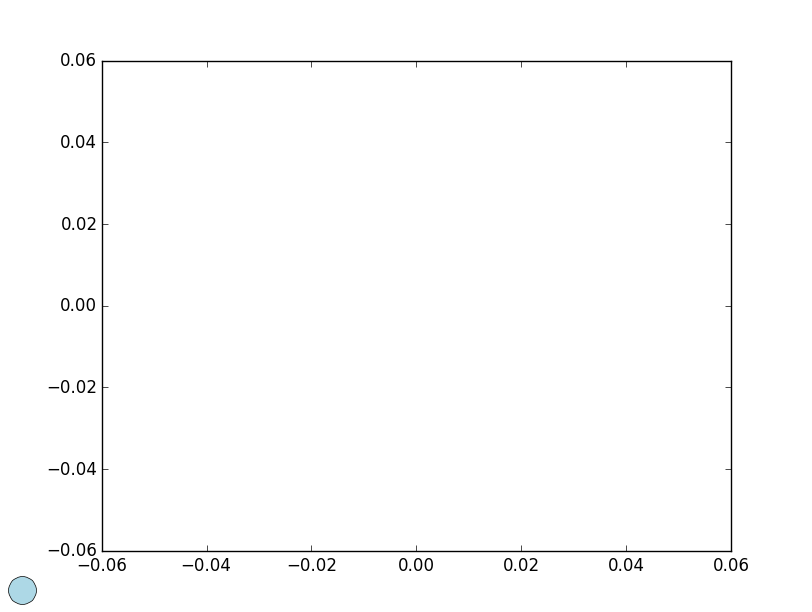
в качестве примера, давайте разместим маркер 30 точек от нижнего левого края рисунок:
import matplotlib.pyplot as plt
from matplotlib.transforms import IdentityTransform
fig, ax = plt.subplots()
points = 30
pixels = fig.dpi * points / 72.0
ax.plot([pixels], [pixels], marker='o', color='lightblue', ms=20,
transform=IdentityTransform(), clip_on=False)
plt.show()
Сочинения Превращает
одна из наиболее полезных вещей о преобразованиях matplotlib заключается в том, что их можно добавить для создания нового преобразования. Это позволяет легко создавать сдвиги.
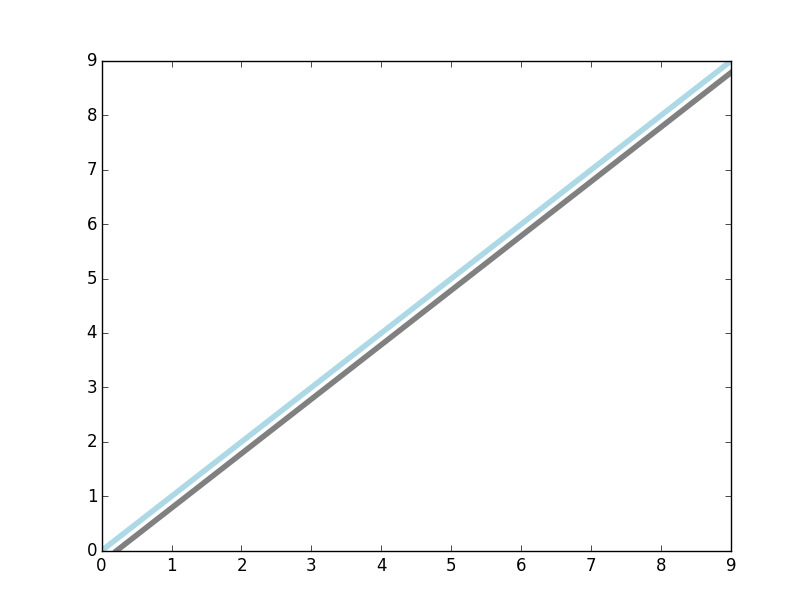
например, давайте построим линию, а затем добавим другую линию, сдвинутую на 15 пикселей в направлении x:
import matplotlib.pyplot as plt
from matplotlib.transforms import Affine2D
fig, ax = plt.subplots()
ax.plot(range(10), color='lightblue', lw=4)
ax.plot(range(10), color='gray', lw=4,
transform=ax.transData + Affine2D().translate(15, 0))
plt.show()
ключевая вещь, котор нужно держать внутри помните, что порядок дополнений имеет значение. Если бы мы это сделали!--12--> вместо этого мы бы сдвинули вещи на 15 сведения единицы вместо 15 пикселей. Добавленные преобразования "прикованы" (составленный был бы более точным термином) по порядку.
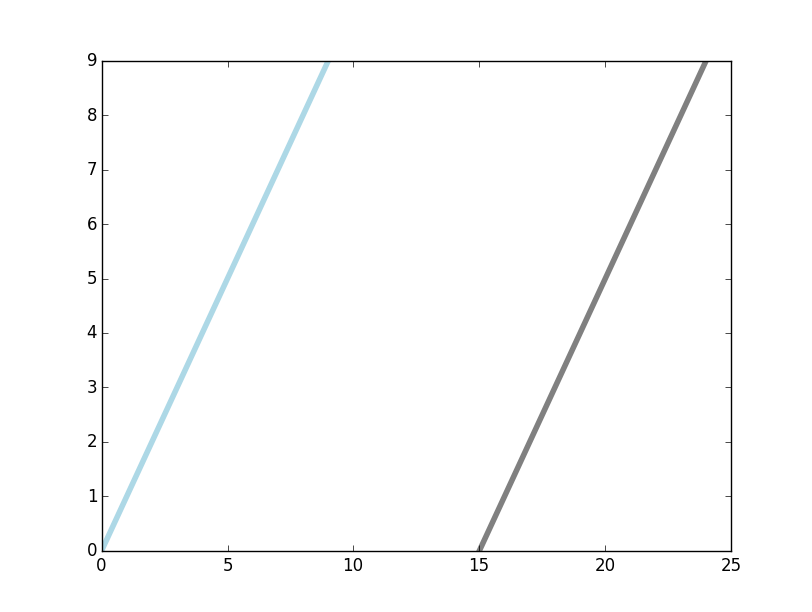
это также позволяет легко определить такие вещи, как "20 пикселей с правой стороны фигуры". Например:
import matplotlib.pyplot as plt
from matplotlib.transforms import Affine2D
fig, ax = plt.subplots()
ax.plot([1, 1], [0, 1], lw=3, clip_on=False, color='salmon',
transform=fig.transFigure + Affine2D().translate(-20, 0))
plt.show()
можно использовать transform ключевое слово для изменения между координатами данных (по умолчанию) и координатами осей. Например:
import matplotlib.pyplot as plt
import matplotlib.lines as lines
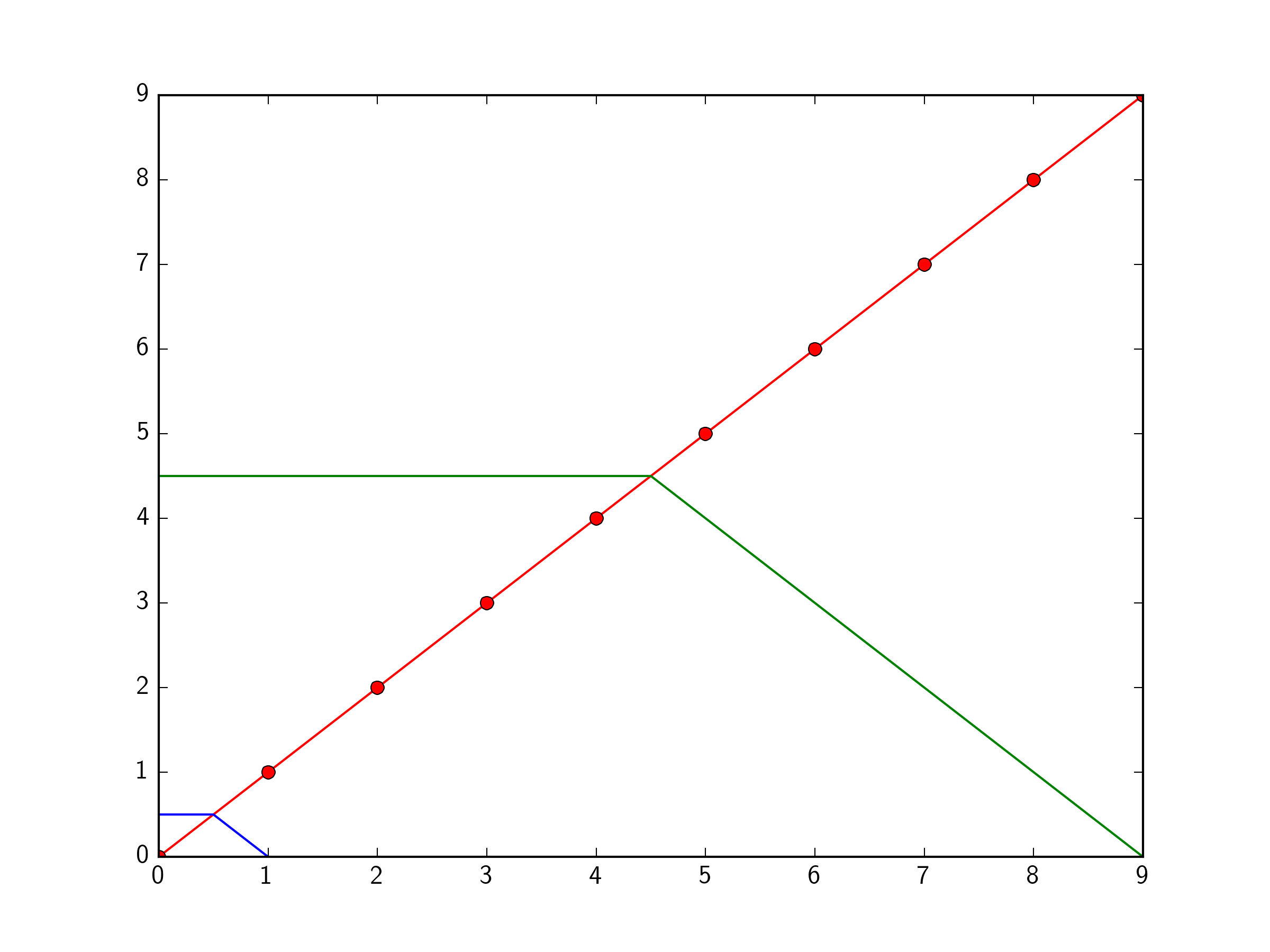
plt.plot(range(10),range(10),'ro-')
myline = lines.Line2D((0,0.5,1),(0.5,0.5,0),color='b') # data coords
plt.gca().add_artist(myline)
mynewline = lines.Line2D((0,0.5,1),(0.5,0.5,0),color='g',transform=plt.gca().transAxes) # Axes coordinates
plt.gca().add_artist(mynewline)
plt.show()