* Эвристика, переоценка / недооценка?

меня смущают термины переоценка / недооценка. Я прекрасно понимаю, как работает алгоритм*, но я не уверен в эффектах эвристики, которая переоценивает или недооценивает.

является ли переоценка, когда вы берете квадрат прямой линии birdview? И почему это делает алгоритм неправильным? Для всех узлов используется одна и та же эвристика.

является ли недооценка, когда вы берете квадрат прямой линии birdview? И почему алгоритм все верно?

Я не могу найти статью, которая объясняет это хорошо и ясно, поэтому я надеюсь, что у кого-то здесь есть хорошее описание.

18
a-star algorithm artificial-intelligence graph search

4 ответов

вы переоцениваете, когда оценка эвристики выше фактической конечной стоимости пути. Вы недооцениваете, когда он ниже (вам не нужно недооценивать, вам просто не нужно переоценивать;правильно оценки отлично). Если стоимость ребра вашего графика равна 1, то приведенные примеры приведут к завышению и недооценке, хотя простое координатное расстояние также работает персиково в декартовом пространстве.

переоценка не совсем сделайте алгоритм "неправильным"; это означает, что у вас больше нет допустимая эвристика, что является условием гарантированного получения a* оптимального поведения. С недопустимой эвристикой алгоритм может сделать тонны лишней работы, исследуя пути, которые он должен игнорировать, и, возможно, найти неоптимальные пути из-за их изучения. Действительно ли это происходит, зависит от вашего проблемного пространства. Это происходит потому, что стоимость пути из joint ' с оценочной стоимостью, что по существу дает алгоритму запутанные идеи о том, какие пути лучше других.

Я не уверен, найдете ли вы его, но вы можете посмотреть на Википедии* статьи. Я упоминаю (и ссылку) в основном потому, что это почти невозможно для Google.

28

с Википедии* статьи, соответствующая часть описания алгоритма:

алгоритм продолжается до тех пор, пока узел цели не будет иметь более низкий f значение, чем любой узел в очереди (или пока очередь не пуста).

ключевая идея заключается в том, что при недооценке A * перестанет исследовать потенциальный путь к цели, как только узнает, что общая стоимость пути превысит стоимость известного пути к цели. Поскольку оценка стоимости пути всегда меньше или равна реальной стоимости пути, a* может отбросить путь, как только оценочная стоимость превышает общую стоимость известного пути.

при переоценке A* понятия не имеет, когда он может прекратить изучение потенциального пути, поскольку могут быть пути с более низкой фактической стоимостью, но более высокой оценочной стоимостью, чем самый лучший в настоящее время известный путь к цели.

9

насколько я знаю, вы хотите обычно недооценивать, чтобы вы все еще могли найти кратчайший путь. Вы можете найти ответ быстрее, переоценивая, но вы можете не найти кратчайший путь. Поэтому переоценка является "неправильной", в то время как недооценка все еще может обеспечить лучшее решение.

Мне жаль, что я не могу дать никакого представления о линиях birdview...

3

короткий ответ:

@chaos ответ немного вводит в заблуждение imo (может быть выделено)

переоценка точно не делает алгоритм "неправильным"; это означает, что у вас больше нет допустимой эвристики, которая является условием гарантированного получения оптимального поведения. С недопустимой эвристикой алгоритм можете в конечном итоге делать тонны лишней работы

как @AlbertoPL намекая

вы можете найти ответ быстрее, переоценивая, но вы не можете найти кратчайший путь.

в конце концов (помимо математического оптимума) оптимальное решение сильно зависит от того, рассматриваете ли вы вычислительные ресурсы, время выполнения, специальные типы "карт"/пространств состояний и т. д.

ответ

в качестве примера я мог бы подумать о приложении в реальном времени, где робот быстрее добирается до цели, используя переоценить эвристическое за время преимущество, начинается раньше больше времени на берется кратчайший путь, но уже не ждет вычислительной данное решение.

чтобы дать вам лучшее впечатление, я делюсь некоторыми образцовыми результатами, которые я быстро создал с Python. Результаты вытекают из одного и того же алгоритма A*, только эвристика отличается. Каждый узел (ячейка сетки) имеет ребра ко всем восьми соседям, кроме стен. Диагональные ребра стоят sqrt (2)=1,41

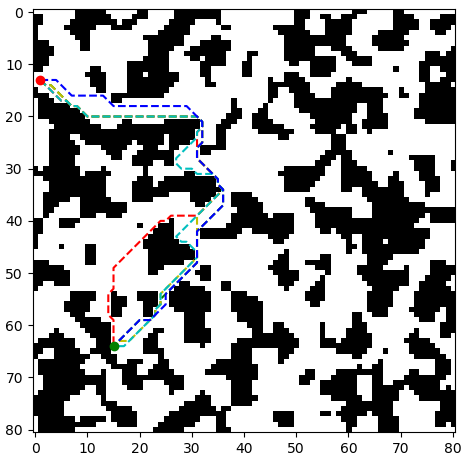
в на первом рисунке показаны возвращаемые пути алгоритма для простого примера. Вы можете увидеть некоторые неоптимальные пути от переоценки эвристики (красный и голубой). С другой стороны, существует несколько оптимальных путей (синий, желтый, зеленый), и это зависит от эвристики, которая найдена первой.

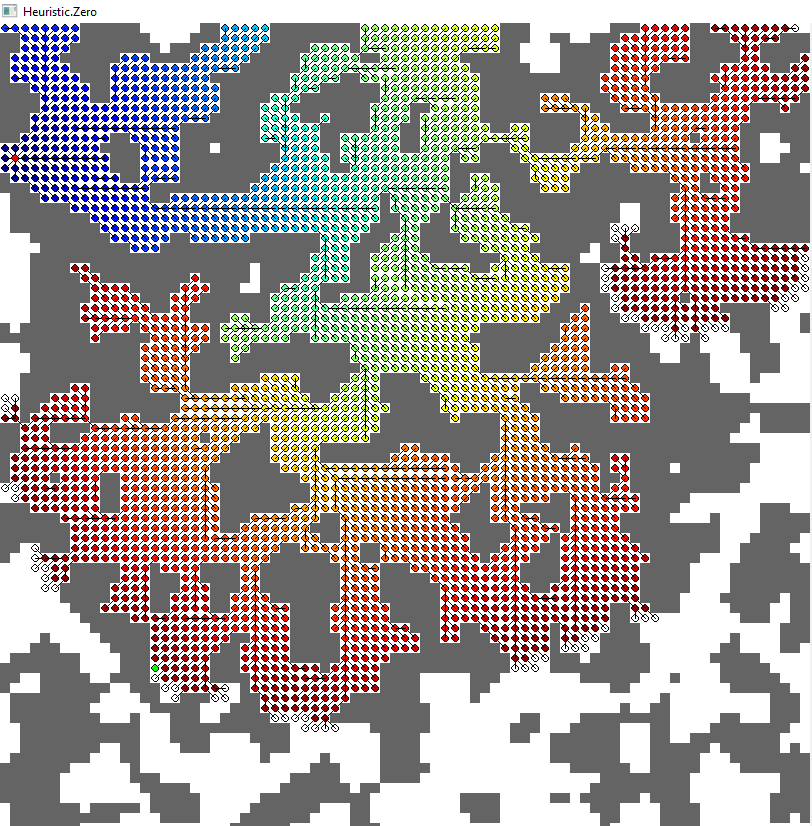
различные изображения показывают все развернутые узлы, когда цель достигнута. Цвет показывает оценочную стоимость пути с использованием этого узла (учитывая" уже принятый " путь от начала до этого узел также; математически это стоимость до сих пор плюс эвристика для этого узла). В любой момент алгоритм расширяет узел с наименьшей оценочной общей стоимостью (описанной выше).

Paths

1. Ноль (синий)

  • соответствует алгоритму Дейкстры
  • узлы расширены: 2685
  • длина пути: 89.669

Zero

2. Как ворона летит (желтый)

3. Идеал (зеленый)

  • кратчайший путь без препятствий (если следовать восьми направлениях)
  • максимально возможная оценка без переоценки (отсюда "идеал")
  • узлы расширены: 854
  • длина пути : 89.669
  • https://i.stack.imgur.com/VqMtF.png

4. Манхэттен!--7--> (красный)

  • кратчайший путь без препятствий (если вы не двигаетесь по диагонали; другими словами: стоимость "перемещения по диагонали" оценивается как 2)
  • переоценивает
  • узлы расширены: 562
  • длина пути : 92.840
  • https://i.stack.imgur.com/gD9t4.png

5. Как ворона летит раз десять (голубой)

2