Фильтр OpenCV Mean / SD

Я бросаю это там в надежде, что кто-то попытается что-то такое смешное раньше. Моя цель-взять входное изображение и сегментировать его на основе стандартного отклонения небольшого окна вокруг каждого пикселя. В принципе, это должно математически напоминать фильтр Гаусса или коробки, поскольку он будет применяться ко времени компиляции (или даже времени выполнения) заданного пользователем размера окна вокруг каждого пикселя, а целевой массив будет содержать информацию SD в каждом пикселе, в изображение того же размера, что и оригинал.

идея состоит в том, чтобы сделать это на изображении в пространстве HSV, чтобы я мог легко найти области однородного цвета (т. е. с небольшими локальными SDs в плоскостях оттенка и Sat) и извлечь их из изображения для более глубокой обработки.

Итак, вопрос в том, кто-нибудь когда-либо строил пользовательский фильтр, как это раньше? Я не знаю, как сделать SD в простом ядре фильтра типа коробки, как те, которые используются для Гаусса и размытия, поэтому я предполагаю Мне придется использовать конструкцию FilterEngine. Кроме того, я забыл упомянуть, что делаю это на C++.

Ваши советы и размышления очень ценятся.

8
filter image-segmentation opencv standard-deviation

1 ответов

Википедия имеет хорошее объяснение стандартное отклонение, который вы можете использовать для фильтра стандартного отклонения.

В основном, это сводится к размыванию изображения с помощью фильтра коробки, размыванию квадрата изображения с помощью фильтра коробки и взятию квадратного корня их разницы.

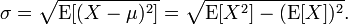
обновление: это, вероятно, лучше показано с уравнением из Википедии... enter image description here

вы можете думать о OpenCV blur функция как представляющая ожидаемое значение (т. е. E[X] a.к. a. выборочное среднее) интересующей окрестности. Случайные выборки X в этом случае представлены пикселями изображения в локальной окрестности. Поэтому, используя приведенную выше эквивалентность, мы имеем что-то вроде sqrt(blur(img^2) - blur(img)^2) в OpenCV. Выполнение этого способа позволяет вычислить локальные средние и стандартные отклонения.

кроме того, на всякий случай вам интересно математическое доказательство. Эта эквивалентность известна как вычислительная формула для дисперсии.

вот как вы можете сделать это в OpenCV:

#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>

using namespace std;
using namespace cv;

Mat mat2gray(const Mat& src)
{
    Mat dst;
    normalize(src, dst, 0.0, 1.0, NORM_MINMAX);
    return dst;
}

int main()
{
    Mat image = imread("coke-can.jpg", 0);

    Mat image32f;
    image.convertTo(image32f, CV_32F);

    Mat mu;
    blur(image32f, mu, Size(3, 3));

    Mat mu2;
    blur(image32f.mul(image32f), mu2, Size(3, 3));

    Mat sigma;
    cv::sqrt(mu2 - mu.mul(mu), sigma);

    imshow("coke", mat2gray(image32f));
    imshow("mu", mat2gray(mu));
    imshow("sigma",mat2gray(sigma));
    waitKey();
    return 0;
}

Это создает следующие изображения:

Оригинал

enter image description here

Mean

enter image description here

Стандартное Отклонение

enter image description here

надеюсь, что это поможет!

29