FindRoot против Solve, NSolve и уменьшает
сначала какой-то несущественный контекст для удовольствия. Мой настоящий вопрос гораздо ниже. Пожалуйста, не трогайте циферблат.
я играю с новыми вероятностными функциями Mathematica 8. Цель состоит в том, чтобы сделать простой анализ мощности. Сила эксперимента равна 1 минус вероятность ошибки типа II (т. е. "никакого эффекта", тогда как в реальности эффект есть).
в качестве примера я выбрал эксперимент, чтобы определить, является ли монета является справедливым. Предположим, вероятность бросать хвосты дано b (Справедливая монета имеет b=0.5), то власть определить, что монета смещена для эксперимента с n монета сальто дается
1 - Probability[-in <= x - n/2 <= in, x [Distributed] BinomialDistribution[n, b]]
С на размер отклонения от ожидаемого среднего для справедливой монеты, которую я готов назвать не подозрительной (на выбирается так, что за честную монету переворачивается n раза количество хвостов будет около 95% времени в течение значит +/- на; это, кстати, определяет размер ошибки типа I, вероятность неправильно утверждать о существовании эффекта).
Mathematica красиво рисует график вычисляемой мощности:
n = 40;
in = 6;
Plot[1-Probability[-in<=x-n/2<=in,x [Distributed] BinomialDistribution[n, b]], {b, 0, 1},
Epilog -> Line[{{0, 0.85}, {1, 0.85}}], Frame -> True,
FrameLabel -> {"P(tail)", "Power", "", ""},
BaseStyle -> {FontFamily -> "Arial", FontSize -> 16,
FontWeight -> Bold}, ImageSize -> 500]
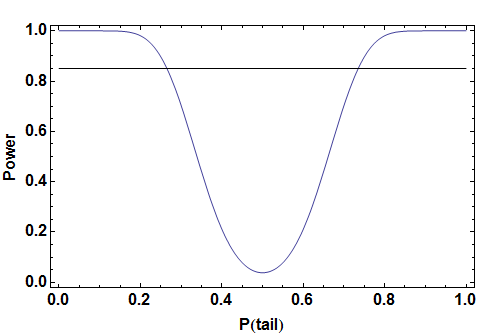
я провел линию мощностью 85%, что обычно считается разумным количеством мощности. Теперь все, что мне нужно, это точки, где кривая мощности пересекается с этой линией. Это говорит мне о минимальном смещении монета должна быть такой, чтобы у меня было разумное ожидание найти ее в эксперименте с 40 сальто.
Итак, я попробовал:
In[47]:= Solve[ Probability[-in <= x - n/2 <= in,
x [Distributed] BinomialDistribution[n, b]] == 0.15 &&
0 <= b <= 1, b]
Out[47]= {{b -> 0.75}}
это терпит неудачу, потому что для b = 0.75 мощность:
In[54]:= 1 - Probability[-in <= x - n/2 <= in, x [Distributed] BinomialDistribution[n, 0.75]]
Out[54]= 0.896768
NSolve находит один и тот же результат. Reduceделает следующее:
In[55]:= res = Reduce[Probability[-in <= x - n/2 <= in,
x [Distributed] BinomialDistribution[n, b]] == 0.15 &&
0 <= b <= 1, b, Reals]
Out[55]= b == 0.265122 || b == 0.73635 || b == 0.801548 ||
b == 0.825269 || b == 0.844398 || b == 0.894066 || b == 0.932018 ||
b == 0.957616 || b == 0.987099
In[56]:= 1 -Probability[-in <= x - n/2 <= in,
x [Distributed] BinomialDistribution[n, b]] /. {ToRules[res]}
Out[56]= {0.85, 0.855032, 0.981807, 0.994014, 0.99799, 0.999965, 1., 1., 1.}
и Reduce удается найти два решения, но он находит немало других, которые умерли не так.
FindRoot работает лучше здесь:
In[57]:= FindRoot[{Probability[-in <= x - n/2 <= in,
x [Distributed] BinomialDistribution[n, b]] - 0.15`}, {b, 0.2, 0, 0.5}]
FindRoot[{Probability[-in <= x - n/2 <= in,
x [Distributed] BinomialDistribution[n, b]] - 0.15`}, {b, 0.8, 0.5, 1}]
Out[57]= {b -> 0.265122}
Out[58]= {b -> 0.734878}
ОК, длинное вступление. Мой вопрос: почему решить, NSolve и уменьшить неудачу так жалко (и молча! здесь? ИМХО, это не может быть численная точность, так как значения мощности, найденные для различных решений, кажутся правильными (они идеально лежат на кривой мощности) и значительно удалены от реального решения.
для mma8-лишенный г-н Волшебник: выражение для власти является тяжелым:
In[42]:= Probability[-in <= x - n/2 <= in,
x [Distributed] BinomialDistribution[n, b]]
Out[42]= 23206929840 (1 - b)^26 b^14 + 40225345056 (1 - b)^25 b^15 +
62852101650 (1 - b)^24 b^16 + 88732378800 (1 - b)^23 b^17 +
113380261800 (1 - b)^22 b^18 + 131282408400 (1 - b)^21 b^19 +
137846528820 (1 - b)^20 b^20 + 131282408400 (1 - b)^19 b^21 +
113380261800 (1 - b)^18 b^22 + 88732378800 (1 - b)^17 b^23 +
62852101650 (1 - b)^16 b^24 + 40225345056 (1 - b)^15 b^25 +
23206929840 (1 - b)^14 b^26
и я не ожидалось Solve справиться с этим, но я возлагал большие надежды на NSolve и Reduce. Обратите внимание, что для n=30, на=5 Solve, NSolve, Reduce и FindRoot все находят одинаковые, правильные решения (конечно, порядок полиномов там ниже).
3 ответов
различные числовые методы будут действовать по-разному при обработке этого.
(1) те, которые находят все корни полиномов, имеют самую сложную работу, поскольку им может потребоваться иметь дело с дефлированными полиномами. FindRoot с крючка есть.
(2) многочлен является возмущением единицы со значительной кратностью. Я ожидал бы, что числовые методы будут иметь проблемы.
(3) корни все в пределах 1-2 порядков величины в размере. Так что это не так далеко из вообще "плохих" многочленов с корнями вокруг единичной окружности.
(4) наиболее сложной является обработка решения[числовой eqn и ineq]. Это должно сочетать методы решения неравенства (т. е. цилиндрическое разложение) с машинной арифметикой. Не ждите пощады. Хорошо, это одномерно, поэтому это сводится к последовательностям штурма или правилу знаков Декарта. Все еще не очень хорошо себя вел.
вот некоторые эксперименты с использованием различных параметров метода.
n = 40; in = 6;
p[b_] := Probability[-in <= x - n/2 <= in,
x \[Distributed] BinomialDistribution[n, b]]
r1 = NRoots[p[b] == .15, b, Method -> "JenkinsTraub"];
r2 = NRoots[p[b] == .15, b, Method -> "Aberth"];
r3 = NRoots[p[b] == .15, b, Method -> "CompanionMatrix"];
r4 = NSolve[p[b] == .15, b];
r5 = Solve[p[b] == 0.15, b];
r6 = Solve[p[b] == 0.15 && Element[b, Reals], b];
r7 = N[Solve[p[b] == 15/100 && Element[b, Reals], b]];
r8 = N[Solve[p[b] == 15/100, b]];
Sort[Cases[b /. {ToRules[r1]}, _Real]]
Sort[Cases[b /. {ToRules[r2]}, _Real]]
Sort[Cases[b /. {ToRules[r3]}, _Real]]
Sort[Cases[b /. r4, _Real]]
Sort[Cases[b /. r5, _Real]]
Sort[Cases[b /. r6, _Real]]
Sort[Cases[b /. r7, _Real]]
Sort[Cases[b /. r8, _Real]]
{-0.128504, 0.265122, 0.728, 1.1807, 1.20794, 1.22063}
{-0.128504, 0.265122, 0.736383, 0.801116, 0.825711, 0.845658, \
0.889992, 0.931526, 0.958879, 0.986398, 1.06506, 1.08208, 1.18361, \
1.19648, 1.24659, 1.25157}
{-0.128504, 0.265122, 0.733751, 0.834331, 0.834331, 0.879148, \
0.879148, 0.910323, 0.97317, 0.97317, 1.08099, 1.08099, 1.17529, \
1.17529, 1.23052, 1.23052}
{-0.128504, 0.265122, 0.736383, 0.801116, 0.825711, 0.845658, \
0.889992, 0.931526, 0.958879, 0.986398, 1.06506, 1.08208, 1.18361, \
1.19648, 1.24659, 1.25157}
{-0.128504, 0.265122, 0.736383, 0.801116, 0.825711, 0.845658, \
0.889992, 0.931526, 0.958879, 0.986398, 1.06506, 1.08208, 1.18361, \
1.19648, 1.24659, 1.25157}
{-0.128504, 0.75}
{-0.128504, 0.265122, 0.734878, 1.1285}
{-0.128504, 0.265122, 0.734878, 1.1285}
Это похоже, NSolve использует NRoots с методом Аберта, и Solve может просто вызывать NSolve.
различные наборы решений, похоже, находятся по всей карте. На самом деле многие из числовых, которые утверждают, что они реальны (но не являются), могут быть не такими плохими. Я буду сравнивать величины одного такого набора против набора, сформированного из нумерации точных корневых объектов (обычно безопасный процесс).
mags4 = Sort[Abs[b /. r4]]
Out[77]= {0.128504, 0.129867, 0.129867, 0.13413, 0.13413, 0.141881, \
0.141881, 0.154398, 0.154398, 0.174443, 0.174443, 0.209069, 0.209069, \
0.265122, 0.543986, 0.543986, 0.575831, 0.575831, 0.685011, 0.685011, \
0.736383, 0.801116, 0.825711, 0.845658, 0.889992, 0.902725, 0.902725, \
0.931526, 0.958879, 0.986398, 1.06506, 1.08208, 1.18361, 1.19648, \
1.24659, 1.25157, 1.44617, 1.44617, 4.25448, 4.25448}
mags8 = Sort[Abs[b /. r8]]
Out[78]= {0.128504, 0.129867, 0.129867, 0.13413, 0.13413, 0.141881, \
0.141881, 0.154398, 0.154398, 0.174443, 0.174443, 0.209069, 0.209069, \
0.265122, 0.543985, 0.543985, 0.575831, 0.575831, 0.685011, 0.685011, \
0.734878, 0.854255, 0.854255, 0.902725, 0.902725, 0.94963, 0.94963, \
1.01802, 1.01802, 1.06769, 1.06769, 1.10183, 1.10183, 1.12188, \
1.12188, 1.1285, 1.44617, 1.44617, 4.25448, 4.25448}
Chop[mags4 - mags8, 10^(-6)]
Out[82]= {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0.00150522, -0.0531384, -0.0285437, -0.0570674, -0.0127339, \
-0.0469044, -0.0469044, -0.0864986, -0.0591449, -0.0812974, \
-0.00263812, -0.0197501, 0.0817724, 0.0745959, 0.124706, 0.123065, 0, \
0, 0, 0}
Даниил Лихтблау
Я думаю, что проблема как раз в числовых instablitity нахождения корней полиномов высокого порядка:
In[1]:= n=40; in=6;
p[b_]:= Probability[-in<=x-n/2<=in,
x\[Distributed]BinomialDistribution[n,b]]
In[3]:= Solve[p[b]==0.15 && 0<=b<=1, b, MaxExtraConditions->0]
1-p[b]/.%
Out[3]= {{b->0.75}}
Out[4]= {0.896768}
In[5]:= Solve[p[b]==0.15 && 0<=b<=1, b, MaxExtraConditions->1]
1-p[b]/.%
Out[5]= {{b->0.265122},{b->0.736383},{b->0.801116},{b->0.825711},{b->0.845658},{b->0.889992},{b->0.931526},{b->0.958879},{b->0.986398}}
Out[6]= {0.85,0.855143,0.981474,0.994151,0.998143,0.999946,1.,1.,1.}
In[7]:= Solve[p[b]==3/20 && 0<=b<=1, b, MaxExtraConditions->0]//Short
1-p[b]/.%//N
Out[7]//Short= {{b->Root[-1+<<39>>+108299005920 #1^40&,2]},{b->Root[<<1>>&,3]}}
Out[8]= {0.85,0.85}
In[9]:= Solve[p[b]==0.15`100 && 0<=b<=1, b, MaxExtraConditions->0]//N
1-p[b]/.%
Out[9]= {{b->0.265122},{b->0.734878}}
Out[10]= {0.85,0.85}
(н. b. MaxExtraConditions->0 на самом деле является опцией по умолчанию, поэтому ее можно было бы исключить из приведенного выше.)
и Solve и Reduce просто генерируя Root объекты
и когда даны неточные коэффициенты, они автоматически оцениваются численно.
Если вы посмотрите на (сокращенный) вывод Out[7] тогда вы увидите Root полного 40-го порядка многочлен:
In[12]:= Expand@(20/3 p[b] - 1)
Out[12]= -1 + 154712865600 b^14 - 3754365538560 b^15 + 43996471155000 b^16 -
331267547520000 b^17 + 1798966820560000 b^18 -
7498851167808000 b^19 + 24933680132961600 b^20 -
67846748661120000 b^21 + 153811663157880000 b^22 -
294248399084640000 b^23 + 479379683508726000 b^24 -
669388358063093760 b^25 + 804553314979680000 b^26 -
834351666126339200 b^27 + 747086226686186400 b^28 -
577064755104364800 b^29 + 383524395817442880 b^30 -
218363285636496000 b^31 + 105832631433929400 b^32 -
43287834659596800 b^33 + 14776188957129600 b^34 -
4150451102878080 b^35 + 942502182076000 b^36 -
168946449235200 b^37 + 22970789150400 b^38 -
2165980118400 b^39 + 108299005920 b^40
In[13]:= Plot[%, {b, -1/10, 11/10}, WorkingPrecision -> 100]
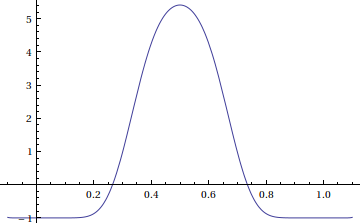
из этого графика вы можете подтвердить, что нули в (приблизительно) {{b - > 0.265122}, {b - > 0.734878}}. Но, чтобы получить плоские части на правой стороне удара, требуется много числовых отмен. Вот как это выглядит без явного :
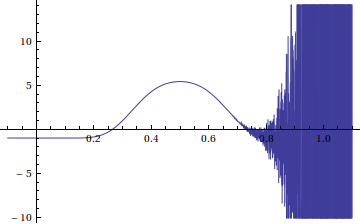
этот график дает понять, почему Reduce (или Solve С MaxConditions->1 см. In[5] выше) находки (слева направо правильно) Первое решение правильно, а второе решение почти правильно, за которым следует целая загрузка crud.
Ну, не правильный ответ, но интересное наблюдение. Solve[ ] имеет такое же поведение, чем Reduce[ ] когда магия (он же MaxExtraConditions опции) используется:
n=40;
in=6;
Solve[Probability[-in<=x-n/2<=in,
x\[Distributed]BinomialDistribution[n,b]]==0.15 &&
0<=b<=1,b, MaxExtraConditions->1]
{{b -> 0.265122}, {b -> 0.736488}, {b -> 0.80151}, {b -> 0.825884},
{b -> 0.84573}, {b -> 0.890444}, {b -> 0.931972}, {b -> 0.960252},
{b -> 0.985554}}
