Формула анимации Ease-in и ease-out

скажите, если я делаю легкость, а затем простота в анимации движения объекта от координаты X1 до координаты X2 по s шагам через равные промежутки времени. Могут ли некоторые предложить формулу для вычисления координат X этого движения?

25
animation c# c++ easing

3 ответов

квадратичная простота, где t = время, b = начальное значение, c = изменение значения, d = длительность:

 function (float time, float startValue, float change, float duration) {
     time /= duration / 2;
     if (time < 1)  {
          return change / 2 * time * time + startValue;
     }

     time--;
     return -change / 2 * (time * (time - 2) - 1) + startValue;
 };

источник: http://gizma.com/easing/

30

На самом деле я бы предпочел использовать функцию, которая получает время в [0; 1] и выводит время в [0; 1], чтобы мы могли применить результат к любому типу (2D-вектор, 3D-вектор,...).

Решение 1

для квадратичного ослабления in / out кривая разделена на две функции в зависимости от t:

  • , когда t f(t) = square(t)
  • , когда t > = 0.5:f(t) = 1 - square(t - 1) + 0.5

после уменьшения, в C, он дал бы это:

float InOutQuadBlend(float t)
{
    if(t <= 0.5f)
        return 2.0f * square(t);
    t -= 0.5f;
    return 2.0f * t * (1.0f - t) + 0.5;
}

Решение 2 (Безье)

еще одна интересная кривая смешивания-это кривая Безье, которая имеет преимущество быть довольно оптимизированной (нет if). Вы можете проверить кривую на Вольфрам. И вот код C:

float BezierBlend(float t)
{
    return square(t) * (3.0f - 2.0f * t);
}

решение 3 (параметрическая функция)

Edit:
Другим методом, предложенным @DannyYaroslavski, является простая формулаздесь.

это является параметрическим и получает хорошее ускорение и замедление in/out.

С alpha = 2 Вы получаете эту функцию:

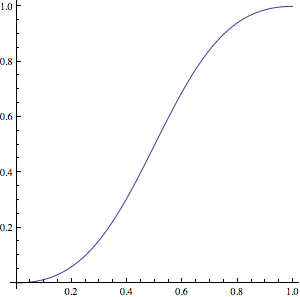
curve

что переводится на C следующим образом:

float ParametricBlend(float t)
{
    float sqt = square(t);
    return sqt / (2.0f * (sqt - t) + 1.0f);
}
29

я получил ту же проблему: хотел оживить мою диаграмму (Ease in-out).

мозговой штурм дал мне два пути:

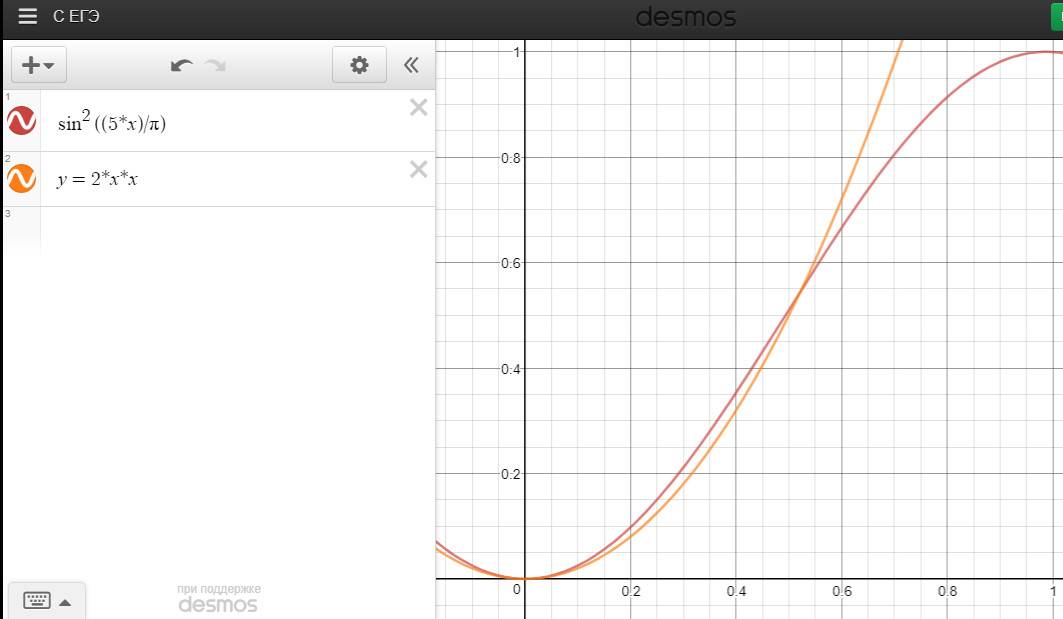
1) Формула Trygonometric. Во-первых, я написал y=(sin(x/π*10-π/2)+1)/2,который аналог sin^2((5*x)/π)

float TrygoEase (float x) {
    float y=(float)Math.pow(Math.sin(5*x/Math.PI),2);
    return y;
}

2) две параболы. Это было нетрудно. Я просто использовал y=2*x*x on [0;0.5] и y=-2(x-1)^2+1 on [0.5;1]

float ParabolEase(float x) {
    float y=2*x*x;
    if(x>0.5f){
        x-=1;
        y=-2*x*x+1;
    }
    return y;
}

используйте эти способы для x=[0;1], что также возвращает y=[0;1].

теперь вы можете сравнить это графики:

enter image description here

0