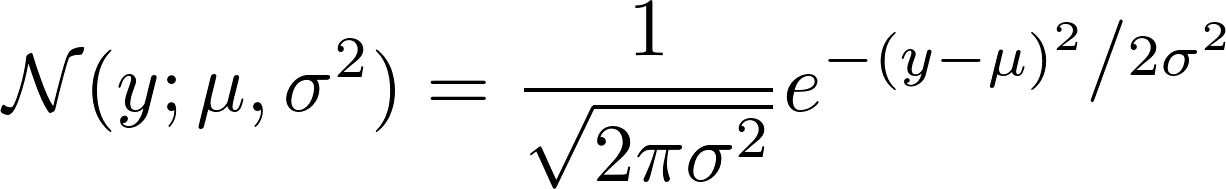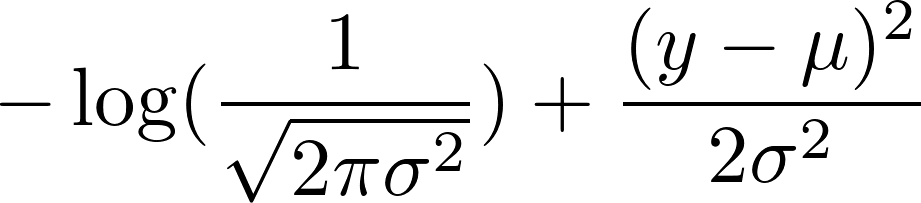Функция затрат для логистической регрессии
в моделях с наименьшими квадратами функция затрат определяется как квадрат разницы между прогнозируемым значением и фактическим значением как функция ввода.
когда мы делаем логистическую регрессию, мы меняем функцию затрат на логирифмическую функцию, вместо того, чтобы определять ее как квадрат разницы между сигмоидной функцией (выходным значением) и фактическим выходом.
нормально изменить и определить нашу собственную функцию цены для того чтобы определить параметры?
4 ответов
Да, вы can определите свою собственную функцию потерь, но если вы новичок, вам, вероятно, лучше использовать один из литературы. Существуют условия, которым должны соответствовать функции потерь:
-
Они должны приближаться к фактической потере, которую вы пытаетесь минимизировать. Как было сказано в другом ответе, стандартные функции потерь для классификации равны нулю-одному потере (скорость классификации), а те, которые используются для обучения классификаторов, являются аппроксимациями эта потеря.
потеря квадратной ошибки от линейной регрессии не используется, потому что она не приближается к нулю-одна-потеря хорошо: когда ваша модель предсказывает +50 для некоторой выборки, в то время как предполагаемый ответ был +1 (положительный класс), прогноз находится на правильной стороне границы решения, поэтому нулевая потеря равна нулю, но потеря квадратной ошибки по-прежнему 492 = 2401. Некоторые алгоритмы обучения будут тратить много времени на получение предсказаний, очень близких к {-1, +1}, вместо того, чтобы сосредоточиться на получении только знак/метка класса справа.(*)
-
функция потерь должна работать с вашим предполагаемым алгоритмом оптимизации. Вот почему ноль-один-убыток не используется напрямую: он не работает с методами оптимизации на основе градиента, поскольку у него нет четко определенного градиента (или даже субградиентного, как потеря шарнира для SVMs имеет).
основной алгоритм, который оптимизирует ноль-один-потери напрямую, является старым перцептрона алгоритм.
кроме того, когда вы подключаете пользовательскую функцию потерь, вы больше не строите модель логистической регрессии, а какой-то другой линейный классификатор.
(*) квадратичную ошибку is используется с линейным дискриминантным анализом, но это обычно решается в близкой форме, а не итеративно.
логистическая функция, шарнир-потеря, приглаженная шарнир-потеря, ЕТК. используются, потому что они являются верхними границами потери двоичной классификации ноль-один.
эти функции, как правило, также наказывают примеры, которые правильно классифицированы, но все еще находятся вблизи границы решения, создавая "маржу"."
Итак, если вы делаете двоичную классификацию, то вы, безусловно, должны выбрать стандартную функцию потерь.
Если вы пытаетесь решить другую проблема, тогда другая функция потери, вероятно, будет работать лучше.
вы не выбираете функцию потери, вы выбираете модель
функция потерь обычно напрямую определяется моделью, когда вы соответствуете своим параметрам, используя оценку максимального правдоподобия (MLE), которая является наиболее популярным подходом в машинном обучении.
Вы упомянули среднюю квадратную ошибку как функцию потерь для линейной регрессии. Затем "мы меняем функцию затрат на логарифмическую функцию", ссылаясь на потерю перекрестной энтропии. Мы не изменили функция стоимости. Фактически, среднеквадратичная ошибка-это поперечная потеря энтропии для линейной регрессии, когда мы предполагаем yнормально распределяется гауссовым, среднее значение которого определяется Wx + b.
объяснение
С MLE вы выбираете параметры таким образом, что вероятность данных обучения максимизируется. Вероятность всего набора данных обучения является продуктом вероятности каждой учебной выборки. Потому что это может underflow к нул, мы обычно максимизировать логарифмическую вероятность обучающих данных / минимизировать отрицательную логарифмическую вероятность. Таким образом, функция затрат становится суммой отрицательной логарифмической вероятности каждой обучающей выборки, которая задается:
-log(p(y | x; w))
где w-параметры нашей модели (включая смещение). Теперь, для логистической регрессии, это логарифм, о котором вы говорили. Но как насчет утверждения, что это также соответствует MSE для линейного регрессия?
пример
чтобы показать, что MSE соответствует кросс-энтропии, мы предполагаем, что y обычно распределяется вокруг среднего значения, которое мы прогнозируем с помощью w^T x + b. Мы также предполагаем, что он имеет фиксированную дисперсию, поэтому мы не предсказываем дисперсию с нашей линейной регрессией, только среднее Гауссова.
p(y | x; w) = N(y; w^T x + b, 1)
вы можете видеть, mean = w^T x + b и variance = 1
теперь функция потерь соответствует к
-log N(y; w^T x + b, 1)
если мы посмотрим, как Гаусс N определено, мы видим:
теперь возьмите отрицательный логарифм этого. Это приводит к:
мы выбрали фиксированную дисперсию 1. Это делает первый член постоянным и уменьшает второй член до:
0.5 (y - mean)^2
теперь помните, что мы определили среднее значение как w^T x + b. Поскольку первый член является постоянным, минимизация отрицательного логарифма Гаусса соответствует минимизации
(y - w^T x + b)^2
что соответствует минимизации среднеквадратичной ошибки.
да, другие функции цены можно использовать для того чтобы определить параметры.
функция квадратов ошибок (обычно используемая функция для линейной регрессии) не очень подходит для логистической регрессии.
как и в случае логистической регрессии, гипотеза нелинейна (сигмовидная функция), что делает функцию квадратной ошибки невыпуклой.
логарифмическая функция является выпуклой функцией, для которой нет локальной optima, поэтому градиентный спуск работает хорошо.