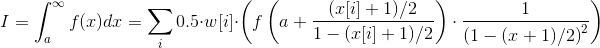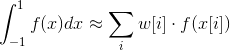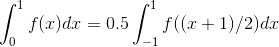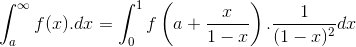Гаусс-Лежандр через интервалы-x - > бесконечность: адаптивный алгоритм эффективного преобразования Весов и узлов

хорошо, я знаю, что это было задано раньше с ограниченным примером для масштабирования [-1, 1] интервалы [a, b] различные интервалы для квадратуры Гаусса-Лежандра в numpy но никто не опубликовал, как обобщить это для [-a, Infinity] (как показано ниже, но не (Пока) быстро). Также это показывает, как вызвать сложную функцию (в количественном ценообразовании опционов) с несколькими реализациями. Есть бенчмарк quad код, за которым следует leggauss со ссылками на примеры кода о том, как реализовать адаптивный алгоритм. Я работал через большинство связанных adaptive algorithm трудности-в настоящее время он печатает сумму разделенного интеграла, чтобы показать, что он работает правильно. Здесь вы найдете функции для преобразования диапазона из [-1, 1] to [0, 1] to [a, Infinity] (спасибо @AlexisClarembeau). Чтобы использовать адаптивный алгоритм, мне пришлось создать другую функцию для преобразования из [-1, 1] to [a, b], который подается обратно в .

import numpy as np
from scipy.stats import norm, lognorm
from scipy.integrate import quad

a = 0
degrees = 50

flag=-1.0000
F = 1.2075
K = 0.1251
vol = 0.43
T2 = 0.0411
T1 = 0.0047

def integrand(x, flag, F, K, vol, T2, T1):
    d1 = (np.log(x / (x+K)) + 0.5 * (vol**2) * (T2-T1)) / (vol * np.sqrt(T2 - T1))
    d2 = d1 - vol*np.sqrt(T2 - T1)
    mu = np.log(F) - 0.5 *vol **2 * T1
    sigma = vol * np.sqrt(T1)
    return lognorm.pdf(x, mu, sigma) * (flag * x*norm.cdf(flag * d1) - flag * (x+K)*norm.cdf(flag * d2))

def transform_integral_0_1_to_Infinity(x, a): 
    return integrand(a+(x/(1-x)), flag, F, K, vol, T2, T1) *(1/(1-x)**2); 

def transform_integral_negative1_1_to_0_1(x, a): 
    return 0.5 * transform_integral_0_1_to_Infinity((x+1)/2, a)

def transform_integral_negative1_1_to_a_b(x, w, a, b):
    return np.sum(w*(0.5 * transform_integral_0_1_to_Infinity(((x+1)/2*(b-a)+a), a)))

def adaptive_integration(x, w, a=-1, b=1, lastsplit=False, precision=1e-10):
    #split the integral in half assuming [-1, 1] range
    midpoint = (a+b)/2
    interval1 = transform_integral_negative1_1_to_a_b(x, w, a, midpoint)
    interval2 = transform_integral_negative1_1_to_a_b(x, w, midpoint, b)
    return interval1+interval2 #just shows this is correct for splitting the interval

def integrate(x, w, a): 
    return np.sum(w*transform_integral_negative1_1_to_0_1(x, a))

x, w = np.polynomial.legendre.leggauss(degrees) 
quadresult = quad(integrand, a, np.Inf, args=(flag, F, K, vol, T2, T1), epsabs=1e-1000)[0]
GL = integrate(x, w, a)
print("Adaptive Sum Result:")
print(adaptive_integration(x, w))
print("GL result"); 
print(GL)
print("QUAD result")
print(quadresult)

еще нужно увеличьте скорость и точность с меньшими размерами, так как я не могу вручную настроить

14
numerical-integration numpy python scipy wolfram-mathematica

2 ответов

Я думаю, что код работает: 

    import numpy as np 
    import math

    deg = 10
    x, w = np.polynomial.legendre.leggauss(deg)

    def function(x): 
        # the function to integrate
        return math.exp(-x)

    def function2(x, a): 
        return function(a+x/(1-x))/((1-x)**2); 

    def anotherOne(x, a): 
        return 0.5 * function2(x/2 + 1/2, a)

    def integrate(deg, a): 
        sum = 0 
        x, w = np.polynomial.legendre.leggauss(deg)
        for i in range(deg): 
            print("sum({}) += {} * {} (eval in {})".format(sum, w[i], anotherOne(x[i], a), x[i]))
            sum += w[i]*anotherOne(x[i], a)
        return sum; 

    print("result"); 
    print(integrate(10, 1))

он объединяет ваше уравнение для интегрирования от a до inf и уравнение для изменения границ интеграла.

Я надеюсь, что это решит вашу проблему (она работает для exp (- x) по крайней мере) :)

Если вы хотите встроенное вычисление, программа делает сумму: enter image description here

Это:

enter image description here

и:

enter image description here

и:

enter image description here

6

в "численное Программирование: практическое руководство для ученых и инженеров, использующих Python и C/C++" Титуса А. Beu, вы можете найти методы в образцах кода integral.py и specfunc.py здесь:http://phys.ubbcluj.ro / ~tbeu/INP/libraries.html вы вызываете функцию xGaussLag(a, deg) которых звонки Laguerre от другого .py файл и возвращает ваш скорректированный (x,w) между a и infinity. Вот как это настроить (Примечание чуть выше deg=80 это очень медленно, я просто показываю вам как применить его, изменив строки выше):

x, w = np.array(xGaussLag(a,deg))
gauss = sum(w * integrand(x, flag, F, K, vol, T2, T1))

получает довольно близкую сходимость на deg=80 (быстрее), но я просто ставлю eps=1e-13 на xGaussLag и оттолкнул deg=150 С этими результатами, тем не менее быстрее, чем quad на 33%:

решение QUADPACK: 0.149221620346 с ошибкой: 1.49870924498 e-12 Гаусс-Лежандр решение: 0.149238273747 Разница между QUADPACK и Gauss-Legendre: 1.66534003601 e-05

в Cython это 6x быстрее, чем прямой Python BTW все еще слишком медленный, поэтому я собираюсь попробовать пакет "FastGL" с ответом от @Alexis на данный момент, просто разместив, как я думаю, это будет полезно для других пользователей SO в будущем.

2