Генерация случайных коррелированных точек x и y с помощью Numpy

Я хотел бы сгенерировать коррелированные массивы координат x и y, чтобы проверить различные подходы построения matplotlib, но я где-то терплю неудачу, потому что я не могу получить numpy.random.multivariate_normal чтобы дать мне образцы, которые я хочу. В идеале я хочу, чтобы мои значения x находились между -0.51 и 51.2, а мои значения y-между 0.33 и 51.6 (хотя я полагаю, что равные диапазоны будут в порядке, так как я могу ограничить график после этого), но я не уверен, что означает (0, 0?) и значения ковариации, которые я должен использовать для получения этих образцов из функция.

14
correlation normal-distribution numpy python random

1 ответов

Как следует из названия numpy.random.multivariate_normal порождает нормальные распределения, это означает, что существует ненулевая вероятность нахождения точек за пределами заданного интервала. Вы можете генерировать коррелированные равномерные распределения, но это немного более запутанно. Взгляните здесь для двух возможных методов.

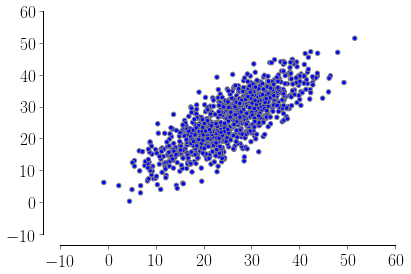
Если вы хотите пойти с нормальным распределением, вы можете настроить Сигмы так, чтобы ваш полуинтервал соответствовал 3 стандартным отклонениям (вы также можете отфильтровать плохое очки при необходимости). Таким образом, у вас будет ~99% ваших очков внутри вашего интервала, например:

import numpy as np
from matplotlib.pyplot import scatter

xx = np.array([-0.51, 51.2])
yy = np.array([0.33, 51.6])
means = [xx.mean(), yy.mean()]  
stds = [xx.std() / 3, yy.std() / 3]
corr = 0.8         # correlation
covs = [[stds[0]**2          , stds[0]*stds[1]*corr], 
        [stds[0]*stds[1]*corr,           stds[1]**2]] 

m = np.random.multivariate_normal(means, covs, 1000).T
scatter(m[0], m[1])

enter image description here

24