Haskell для лямбда-исчисления, тип выведения
мое приключение в программировании Haskell не было эпическим. Я реализую простое лямбда-исчисление, и я рад, что закончил Syntax, Evaluation, а также Substitution, надеясь, что они правильные. Остается typing как определено внутри красной коробки (на рисунке ниже), для которого я ищу руководство.
заголовок
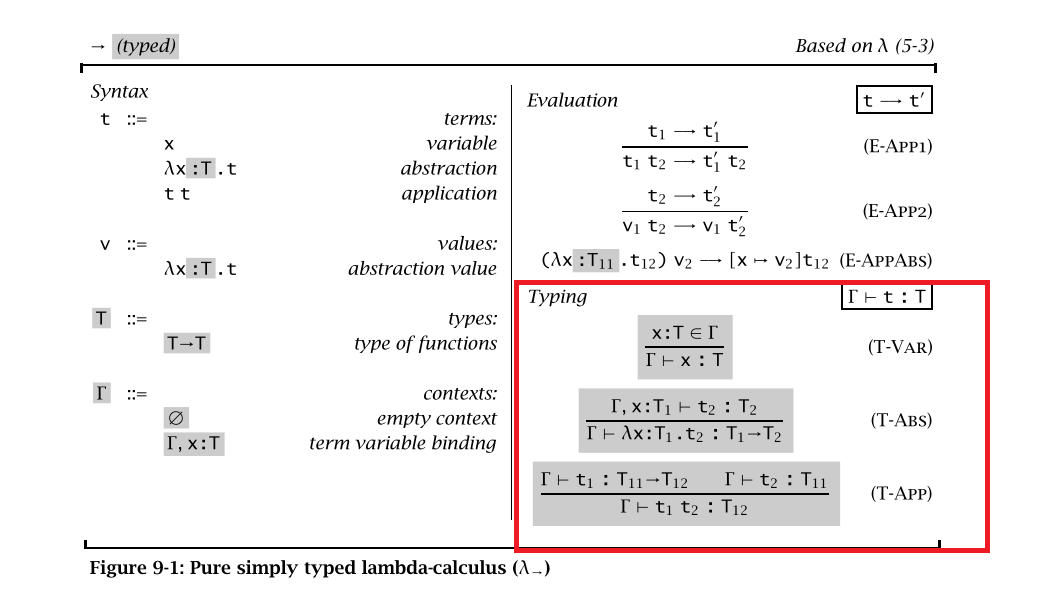
пожалуйста, поправьте меня, если я ошибаюсь,
(1) но я понял, что (T-Var), возвращает тип данных переменной x. Какая конструкция в Haskell возвращает type ? Я знаю это в prelude это :t x, но я ищу тот, который работает под main = do.
(2) Если бы я должен был определить функцию type_of, скорее всего, мне нужно определить ожидаемый и возвращаемый тип, в качестве примера,
type_of (Var x) :: type1 -> type2
type1 должно быть общим и type2 должен быть любым типом объекта, который хранит информацию о типе переменной. Ради этого я потерян. о том, как определить type1 и type2.
(3) для (T-APP) и (T-ABS), я предполагаю, что применяю замену на Abstraction String Lambda и Application Lambda Lambda соответственно. Тип сокращенной формы-возвращаемый тип. Это верно?
спасибо заранее...
2 ответов
ключевая вещь, которую нужно забрать из просто типизированного лямбда-исчисления, заключается в том, что типы аннотируются на самих лямбда-связывателях, каждый лямбда-термин имеет тип. Правила набора текста, которые предоставляет Пирс, - это как механически type-check что выражение хорошо набирается. вывод типа это тема, которую он охватывает позже в книге, которая восстанавливает типы из нетипизированных выражений.
в стороне, что Пирс не дает в этом примере пара типов грунта (Bool, Int), которые полезны при реализации алгоритма, поэтому мы просто добавим их к нашему определению.
t = x
| λ x : T . t
| t t
| <num>
| true
| false
T = T -> T
| TInt
| TBool
если мы переведем это в Haskell, мы получим:
type Sym = String
data Expr
= Var Sym
| Lam Sym Type Expr
| App Expr Expr
| Lit Ground
deriving (Show, Eq, Ord)
data Ground = LInt Int
| LBool Bool
deriving (Show, Eq, Ord)
data Type = TInt
| TBool
| TArr Type Type
deriving (Eq, Read, Show)
на Γ это прокалывает потоки через уравнения для среды типа, которую мы можем представить в Haskell как простую структуру списка.
type Env = [(Sym, Type)]
пустая среда Ø затем просто []. Когда Пирс пишет Γ, x : T ⊢ ... он имеет в виду среду, расширенную с определением x привязан к типу T. В Haskell мы бы реализовали его следующим образом:
extend :: Env -> (Sym, Type) -> Env
extend env xt = xt : env
чтобы написать проверку из TAPL, мы реализуем небольшой стек монады ошибок.
data TypeError = Err String deriving Show
instance Error TypeError where
noMsg = Err ""
type Check a = ErrorT TypeError Identity a
check :: Env -> Expr -> Check Type
check _ (Lit LInt{}) = return TInt
check _ (Lit LBool{}) = return TBool
-- x : T ∈ Γ
-- ----------
-- Γ ⊦ x : T
check env (Var x) = case (lookup x env) of
Just e -> return e
Nothing -> throwError $ Err "Not in Scope"
-- Γ, x : T ⊦ e : T'
-- --------------------
-- Γ ⊦ λ x . e : T → T'
check env (Lam x t e) = do
rhs <- (check (extend env (x,t)) e)
return (TArr t rhs)
-- Γ ⊦ e1 : T → T' Γ ⊦ e2 : T
-- ----------------------------
-- Γ ⊦ e1 e2 : T'
check env (App e1 e2) = do
t1 <- check env e1
t2 <- check env e2
case t1 of
(TArr t1a t1r) | t1a == t2 -> return t1r
(TArr t1a _) -> throwError $ Err "Type mismatch"
ty -> throwError $ Err "Trying to apply non-function"
runCheck :: Check a -> Either TypeError a
runCheck = runIdentity . runErrorT
checkExpr :: Expr -> Either TypeError Type
checkExpr x = runCheck $ check [] x
когда мы называем checkExpr в выражении мы либо возвращаем допустимый тип выражения, либо TypeError указывает, что не так с функцией.
например, если мы имеем термин:
(λx : Int -> Int . x) (λy : Int. y) 3
App (App (Lam "x" (TArr TInt TInt) (Var "x")) (Lam "y" TInt (Var "y"))) (Lit (LInt 3))
мы ожидаем, что наш type checker подтвердит, что он имеет тип вывода TInt.
но не, например:
(λx : Int -> Int . x) 3
App (Lam "x" (TArr TInt TInt) (Var "x")) (Lit (LInt 3))
С TInt не равно (TInt -> TInt).
это все, что действительно нужно для проверки STLC.
в принципе. Я считаю, что это из TAPL (это похоже на таблицу из TAPL, по крайней мере), поэтому есть глава, посвященная алгоритмической проверке типов. Но это по существу идет как
typeOf :: TypeEnv -> Term -> Type
typeOf typeEnv (Var x) = x `lookup` typeEnv
typeOf typeEnv (Abs var ty x) = ty `Arrow` typeOf ((x, ty) `extending` typeEnv) x
typeOf typeEnv (App f arg) = case typeOf f of
Arrow inp out | inp == argT -> out
_ -> Fail Some How
where argT = typeOf typeEnv arg
поэтому мы бросаем вокруг этого типа среды и расширить его, как мы идем. Правила набора текста здесь легко перевести в алгоритм, потому что они точно соответствуют синтаксису. Например, на срок M существует ровно одно правило с выводом, что Env |- M : T.
это становится намного сложнее, когда это не так, например, субтипы.
