HTML5 Canvas: вычисление точки x, y при повороте
Я разрабатываю приложение HTML5 Canvas, и оно включает в себя чтение xml-файла, который описывает положение стрелок, прямоугольников и других фигур, которые мне нужно нарисовать на холсте.
пример XML-макета:
<arrow left="10" top="20" width="100" height="200" rotation="-40" background-color="red"/>
<rect left="10" top="20" width="100" height="200" rotation="300" background-color="red"/>
если объект вращается, он включает в себя вычисление положения точки(называемой P новое положение объекта после вращения) при вращении вокруг другой точки (слева,сверху). Я пытаюсь придумать общую функцию / формулу, которую я могу использовать для вычислите эту точку P, но моя математика немного слаба, и я не могу определить, какую формулу дуги/касательной я должен использовать.
можете ли вы помочь мне придумать формулу, которую я могу использовать для вычисления точки P для вращений, которые могут быть как положительными, так и отрицательными?
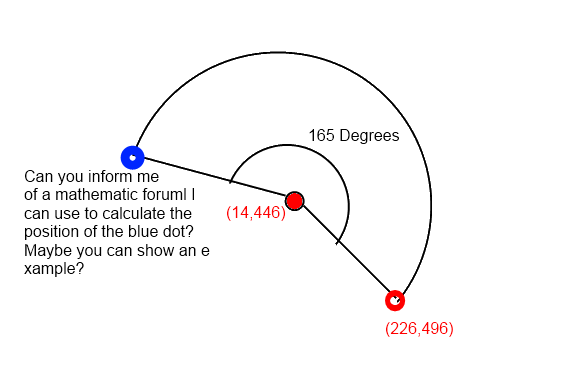
в приведенном выше примере: точка (14,446) - левая, верхняя точка и точка (226,496) - средняя точка объекта, когда она не вращается, поэтому точка=(левая + ширина / 2, верхняя + высота / 2) и синий точка-это средняя точка при вращении. Я знаю, как вычислить длину линии между точками (14,446) & (226,496), но не как вычислить синюю точку x, позицию y - кстати: длина этой линии такая же, как линия между синей точкой & (14,446)
len = sqrt( (496-446)^2 + (226-14)^2 );
= 227.56;
3 ответов
Это довольно просто. При вращении вокруг начала координат системы координат для угла тета координаты (x,y) изменяются как
x' = x * cos(Theta) - y * sin(Theta);
y' = x * sin(Theta) + y * cos(Theta);
Итак, все, что вам нужно, это перевести точку вращения в одну из точек, которые у вас есть. Давайте напишем его более простым способом: (x1,y1) = (14,446) и (x2,y2) = (226,496). Вы пытаетесь "вращать" (x2,y2) вокруг (x1,y1). Вычислить (dx2,dy2) в новой системе координат с началом в (x1, y1).
(dx2,dy2) = (x2-x1,y2-y1);
теперь поворот (положительные углы против часовой стрелки):
dx2' = dx2 * cos(165 Degrees) - dy2 * sin(165 Degrees);
dy2' = dx2 * sin(165 Degrees) + dy2 * cos(165 Degrees);
последний шаг-перевести координаты точки из начала координат в (x1, y1) обратно в исходное (0,0);
x2' = dx2' + x1;
y2' = dy2' + y1;
ps: Читайте также это:)http://en.wikipedia.org/wiki/Rotation_matrix и не забывайте, что большинство тригонометрических функций в разных языках программирования имеют дело в основном с радианами..
pps: и я надеюсь, что я не напугал вас-спросите, если у вас есть вопросы.
Я думаю, что в вашем случае вы должны быть в состоянии рассчитать это положение вращения со следующей системой уравнений:
x = R * Math.cos(angle - angle0);
y = R * Math.sin(angle - angle0);
angle = deg * Math.PI / 180;
angle0 = Math.atan(y0/x0);
R длина вектора радиуса yor (len в вашем примере).deg угол в градусах повороте, я.г 120°x и y координаты конечной позиции, которую вы ищете.angle - фактический угол поворота (в радианах, а не Грады).angle0 - это начальная точка угла вращается относительно оси абсцисс. Нам нужно предварительно вычислить его с помощью Math.atan.
не проверял. Так что попробуй. Но идея такая же - использовать тригонометрические функции.
