Ирегулярный график кластеризации k-средних, удаление выбросов
Привет я работаю над попыткой кластеризации сетевых данных из набора данных darpa 1999 года. К сожалению, я не получаю кластеризованных данных, по сравнению с некоторыми из литературы, используя те же методы и методы.
мои данные выходят так:
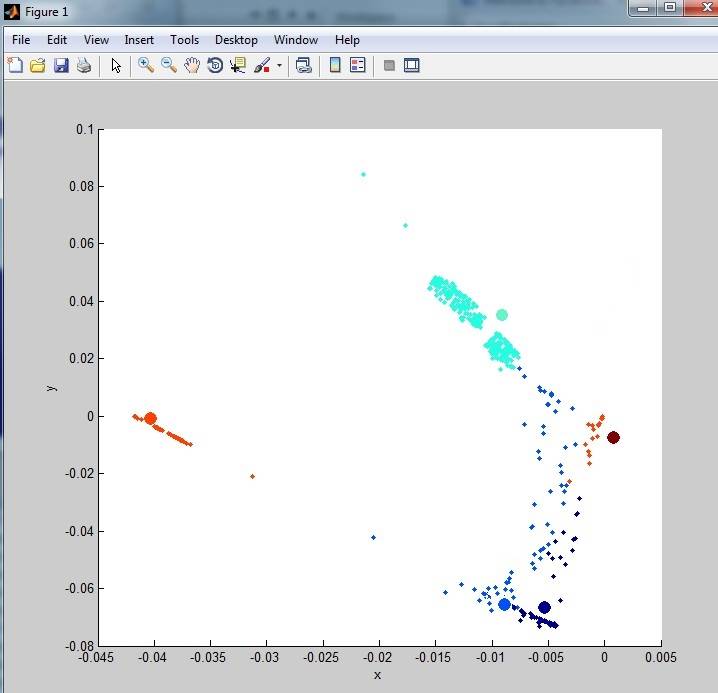
как вы можете видеть, он не очень Кластеризован. Это связано с большим количеством выбросов (шума) в наборе данных. Я посмотрел на некоторые методы удаления выбросов, но ничего я не пробовал до сих пор действительно очищает данные. Один из методов, которые я пробовал:
%% When an outlier is considered to be more than three standard deviations away from the mean, determine the number of outliers in each column of the count matrix:
mu = mean(data)
sigma = std(data)
[n,p] = size(data);
% Create a matrix of mean values by replicating the mu vector for n rows
MeanMat = repmat(mu,n,1);
% Create a matrix of standard deviation values by replicating the sigma vector for n rows
SigmaMat = repmat(sigma,n,1);
% Create a matrix of zeros and ones, where ones indicate the location of outliers
outliers = abs(data - MeanMat) > 3*SigmaMat;
% Calculate the number of outliers in each column
nout = sum(outliers)
% To remove an entire row of data containing the outlier
data(any(outliers,2),:) = [];
при первом запуске он удалил 48 строк из 1000 нормализованных случайных строк, выбранных из полного набора данных.
Это полный скрипт, который я использовал для данных:
%% load data
%# read the list of features
fid = fopen('kddcup.names','rt');
C = textscan(fid, '%s %s', 'Delimiter',':', 'HeaderLines',1);
fclose(fid);
%# determine type of features
C{2} = regexprep(C{2}, '.$',''); %# remove "." at the end
attribNom = [ismember(C{2},'symbolic');true]; %# nominal features
%# build format string used to read/parse the actual data
frmt = cell(1,numel(C{1}));
frmt( ismember(C{2},'continuous') ) = {'%f'}; %# numeric features: read as number
frmt( ismember(C{2},'symbolic') ) = {'%s'}; %# nominal features: read as string
frmt = [frmt{:}];
frmt = [frmt '%s']; %# add the class attribute
%# read dataset
fid = fopen('kddcup.data_10_percent_corrected','rt');
C = textscan(fid, frmt, 'Delimiter',',');
fclose(fid);
%# convert nominal attributes to numeric
ind = find(attribNom);
G = cell(numel(ind),1);
for i=1:numel(ind)
[C{ind(i)},G{i}] = grp2idx( C{ind(i)} );
end
%# all numeric dataset
fulldata = cell2mat(C);
%% dimensionality reduction
columns = 6
[U,S,V]=svds(fulldata,columns);
%% randomly select dataset
rows = 1000;
columns = 6;
%# pick random rows
indX = randperm( size(fulldata,1) );
indX = indX(1:rows)';
%# pick random columns
indY = indY(1:columns);
%# filter data
data = U(indX,indY);
% apply normalization method to every cell
maxData = max(max(data));
minData = min(min(data));
data = ((data-minData)./(maxData));
% output matching data
dataSample = fulldata(indX, :)
%% When an outlier is considered to be more than three standard deviations away from the mean, use the following syntax to determine the number of outliers in each column of the count matrix:
mu = mean(data)
sigma = std(data)
[n,p] = size(data);
% Create a matrix of mean values by replicating the mu vector for n rows
MeanMat = repmat(mu,n,1);
% Create a matrix of standard deviation values by replicating the sigma vector for n rows
SigmaMat = repmat(sigma,n,1);
% Create a matrix of zeros and ones, where ones indicate the location of outliers
outliers = abs(data - MeanMat) > 2.5*SigmaMat;
% Calculate the number of outliers in each column
nout = sum(outliers)
% To remove an entire row of data containing the outlier
data(any(outliers,2),:) = [];
%% generate sample data
K = 6;
numObservarations = size(data, 1);
dimensions = 3;
%% cluster
opts = statset('MaxIter', 100, 'Display', 'iter');
[clustIDX, clusters, interClustSum, Dist] = kmeans(data, K, 'options',opts, ...
'distance','sqEuclidean', 'EmptyAction','singleton', 'replicates',3);
%% plot data+clusters
figure, hold on
scatter3(data(:,1),data(:,2),data(:,3), 5, clustIDX, 'filled')
scatter3(clusters(:,1),clusters(:,2),clusters(:,3), 100, (1:K)', 'filled')
hold off, xlabel('x'), ylabel('y'), zlabel('z')
grid on
view([90 0]);
%% plot clusters quality
figure
[silh,h] = silhouette(data, clustIDX);
avrgScore = mean(silh);
Это два различных кластера от выходных данных:
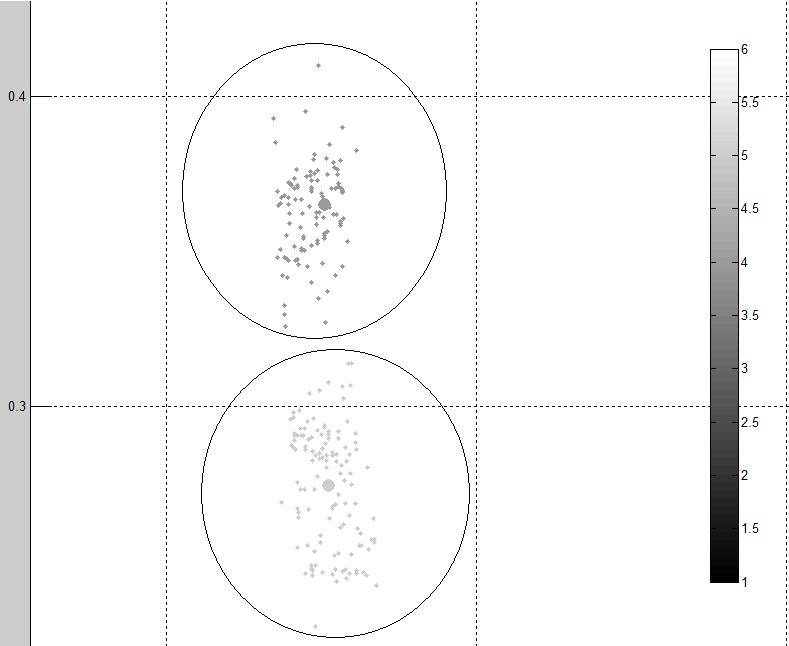
как вы можете видеть данные выглядят чище и более сгруппированы, чем оригинал. Однако я все еще думаю, что лучший метод может использовать.
например, наблюдая за общей кластеризацией, у меня все еще есть много шума (выбросов) из набора данных. Как видно здесь:
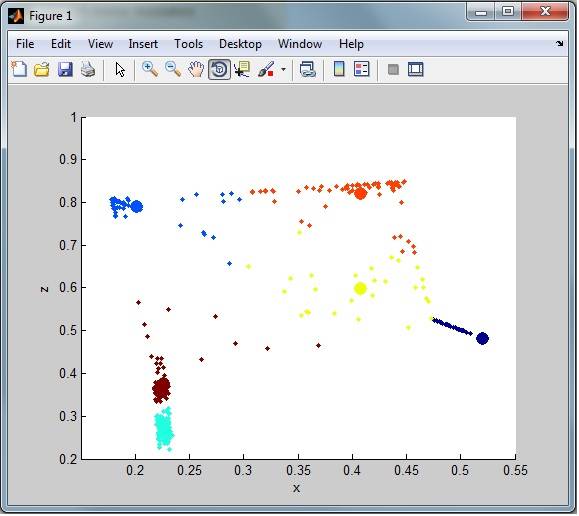
мне нужны строки выбросов, помещенные в отдельный набор данных для последующей классификации (только удаленные из кластеризации)
вот ссылка на набор данных darpa, обратите внимание, что набор данных 10% имел значительное сокращение столбцов, большинство столбцов, которые имеют 0 или 1 работает сквозные были удалены (42 столбца до 6 столбцов):
http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html
редактировать
столбцы, хранящиеся в наборе данных:
src_bytes: continuous.
dst_bytes: continuous.
count: continuous.
srv_count: continuous.
dst_host_count: continuous.
dst_host_srv_count: continuous.
ИЗМЕНИТЬ:
основываясь на обсуждениях с Анони-муссом и его ответом, может быть способ уменьшения шума в кластеризации с помощью K-Медоидов http://en.wikipedia.org/wiki/K-medoids. Я ... надеясь, что в коде, который у меня сейчас есть, не так много изменений, но пока я не знаю, как его реализовать, чтобы проверить, значительно ли это уменьшит шум. Поэтому, если кто-то может показать мне рабочий пример, это будет принято в качестве ответа.
2 ответов
во-первых: вы просите много здесь. Для дальнейшего использования: попробуйте разбить свою проблему на более мелкие куски и опубликовать несколько вопросов. Это увеличивает ваши шансы получить ответы (и не стоит вам 400 репутации!).
к счастью для вас, я понимаю ваше затруднительное положение, и просто люблю такого рода вопрос!
помимо возможных проблем этого набора данных с k-means, этот вопрос по-прежнему является достаточно общим для применения также к другим наборам данных (и, таким образом, гуглеры заканчивают здесь, ища аналогичную вещь), поэтому давайте продолжим и решим это.
Я предлагаю изменить этот ответ, пока вы не получите достаточно удовлетворительные результаты.
число кластеров
Шаг 1 любой проблемы кластеризации: сколько кластеров выбрать? Я знаю несколько методов, с помощью которых вы можете выбрать нужное количество кластеров. Есть хороший вики-страницы об этом, содержащем все методы ниже (и еще несколько).
визуальный осмотр
это может показаться глупым, но если у вас есть хорошо разделенные данные, простой график может сказать вам уже (приблизительно), сколько кластеров вам понадобится, просто посмотрев.
плюсы:
- быстрая
- простой
- хорошо работает на хорошо разделенных кластерах в относительно небольших наборах данных
плюсы:
- и грязный
- требуется взаимодействие с пользователем
- легко пропустить меньшие кластеры
- данные с менее хорошо разделенными кластерами или очень многими из них трудно сделать этим методом
- это все довольно субъективно ... следующий человек может выбрать другую сумму, чем вы.
силуэты участка
как указано в одном из ваших другие вопросы, сделав silhouettes сюжет поможет вам сделать лучшее решение о количестве кластеров в данных.
плюсы:
- относительно простой
- уменьшает субъективность путем использование статистических измерений
- интуитивный способ представления качества выбора
плюсы:
- требуется взаимодействие с пользователем
- в пределе, если вы берете столько кластеров, сколько есть точек данных, график силуэтов скажет вам, что это самый лучший выбор
- это все еще довольно субъективно, не основано на статистических средствах
- может быть в вычислительном отношении дорого
способ локтевых
как и при подходе к сюжету силуэтов, вы запускаете kmeans неоднократно, каждый раз с большим количеством кластеров, и вы увидите, сколько всего разница в данных объясняется кластеров выбирают этот kmeans run. Будет несколько кластеров, где количество объясненной дисперсии внезапно увеличится намного меньше, чем в любом из предыдущих вариантов количества кластеров ("локоть"). Локоть тогда статистически говоря лучший выбор для количества кластеров.
плюсы:
- не требуется взаимодействие с пользователем -- локоть может быть выбран автоматически
- статистически больше звука, чем любой из вышеупомянутых методы
плюсы:
- несколько сложнее
- еще субъективно, так как определение "локоть" зависит от субъективно выбранных параметров
- может быть в вычислительном отношении дорого
останцы
после того, как вы выбрали количество кластеров с любым из методов выше, пришло время сделать обнаружение выбросов, чтобы увидеть, если качество ваших кластеров улучшает.
Я бы начал с двухэтапного итеративного подхода, используя метод локтя. В псевдо-Matlab:
data = your initial dataset
dataMod = your initial dataset
MAX = the number of clusters chosen by visual inspection
while (forever)
for N = MAX-5 : MAX+5
if (N < 1), continue, end
perform k-means with N clusters on dataMod
if (variance explained shows a jump)
break
end
if (you are satisfied)
break
end
for i = 1:N
extract all points from cluster i
find the centroid (let k-means do that)
calculate the standard deviation of distances to the centroid
mark points further than 3 sigma as possible outliers
end
dataMod = data with marked points removed
end
жесткая часть, очевидно, определяет, является ли you are satisfied.
Это ключ к эффективности алгоритма. Грубая структура
эта часть
if (you are satisfied)
break
end
было бы что-то вроде этого
if (situation has improved)
data = dataMod
elseif (situation is same or worse)
dataMod = data
break
end
на situation has improved когда меньше выбросов или дисперсия
explaned для всех вариантов N лучше, чем во время предыдущий цикл в while. С этим тоже стоит повозиться.
в любом случае, гораздо больше, чем первая попытка, я бы не назвал это. Если кто-то увидит здесь incompletenesses, недостатки или пробелы, пожалуйста комментировать или редактировать.
обратите внимание, что использование этого набора данных уныние:
набор данных имеет ошибки: набор данных KDD Cup '99 (сетевое вторжение) считается вредным
пересмотреть, используя другой алгоритм. k-means не подходит для данных смешанного типа, где многие атрибуты дискретные, и имеют очень разные масштабы. K-means должен иметь возможность вычислять разумный средства. И для двоичного вектора "0.5" - это не разумное значение, оно должно быть либо 0, либо 1.
кроме того, k-means не слишком любит выбросы.
при построении графика обязательно масштабируйте их одинаково, иначе результат будет выглядеть неверно. Ваша ось X имеет длину около 0,9, ваша ось y только 0,2-неудивительно, что они выглядят раздавленными.
в целом, может быть, набор данных просто не имеет кластеров в стиле k-means? вы определенно должны попробовать методы на основе плотности (потому что эти can сделки с выбросы), такие как DBSCAN. Но, судя по добавленным вами визуализациям, я бы сказал, что у него не более 4-5 кластеров, и они не очень интересны. Вероятно, они могут быть захвачены с несколькими порогами в некоторых измерениях.
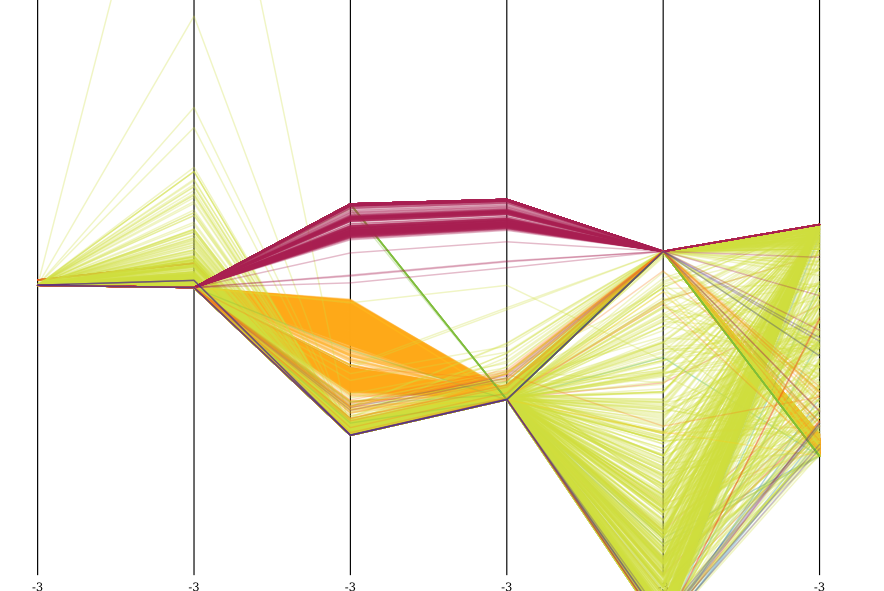
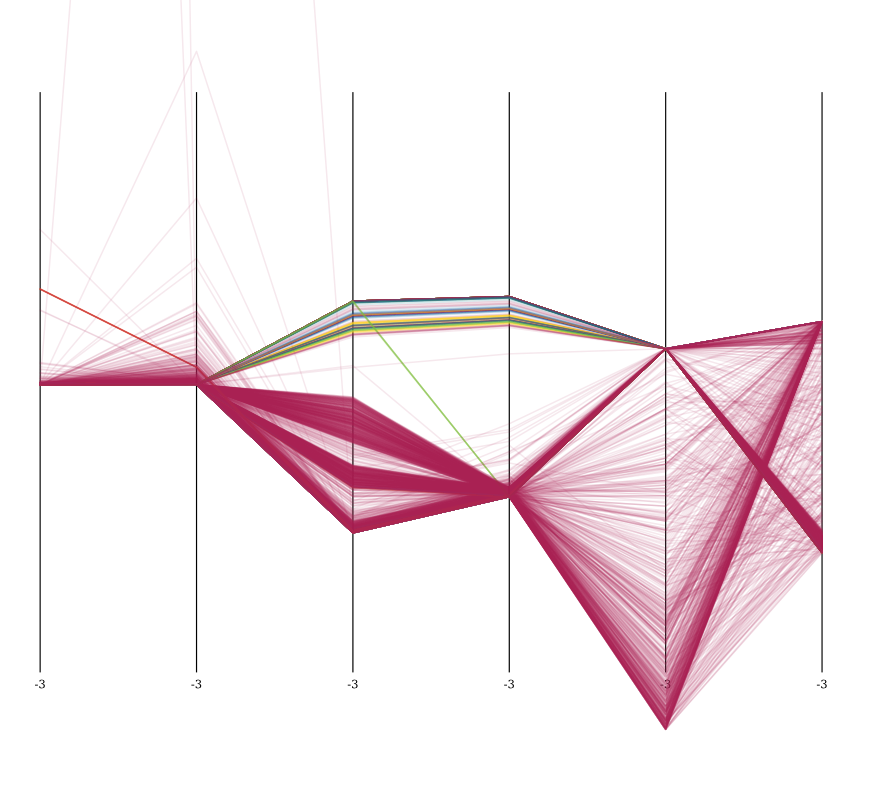
здесь визуализация набора данных после Z-нормализации, визуализированного в параллельных координатах, с 5000 образцами. Ярко-зеленый-это нормально.
вы можете ясно видеть специальные свойства набора данных. Все атаки явно различаются по атрибутам 3 и 4 (count и srv_count), а также наиболее сконцентрированы в dst_host_count и dst_host_srv_count.
Я тоже запустил оптику на этом наборе данных. Он обнаружил несколько кластеров, большинство из которых были окрашены в винный цвет. Но они не очень интересны. Если у вас есть 10 разных хостов ping-flooding, они образуют 10 кластеров.
вы можете очень хорошо видеть, что оптика управлял сгруппировать несколько таких атак. Он пропустил все оранжевое вещество (возможно, если бы я установил minpts ниже, он довольно распространен), но он даже обнаружил *структуру внутри атаки винного цвета), разбив ее на несколько отдельных событий.
до действительно смысл этого набора данных, вы должны начните с извлечения функции, например, путем слияния таких попыток соединения ping flood в совокупный событие.
Также обратите внимание, это это нереалистичный сценарий.
- есть хорошо известные шаблоны, связанные с атаками, в частности сканирование портов. Они лучше всего обнаруживаются с помощью специализированного детектора сканирования портов, а не с обучение.
- смоделированные данные имеют много совершенно бессмысленных "атак", смоделированных. Например атака Smurf из 90-х годов составляет >50% от набора данных, а SYN flood-еще 20%; в то время как нормальный трафик это
- для такого рода атак, есть известные подписи.
- большая часть современных атак (например, SQL-инъекция) протекает с обычным HTTP-трафиком и не будет отображаться аномально в шаблоне raw-трафика.
просто не используйте эти данные для классификации или обнаружения выбросов. Просто не надо.
цитируя ссылку KDNuggets выше:
в результате, мы настоятельно рекомендуем
(1) все исследователи перестают использовать набор данных KDD Cup '99,
(2) веб-сайты KDD Cup и UCI включают предупреждение на веб-странице набора данных KDD Cup '99, информирующее исследователей о том, что существуют известные проблемы с набором данных, и
(3) рецензенты для конференций и журналов Ding документы (или даже прямо отклонение их, как это принято в сообществе сетевой безопасности) с результатами, полученными исключительно из набора данных KDD Cup '99.
это не реальные, ни реалистичная данные. Иди что-то другое.
