Использование CUDA для решения системы уравнений нелинейным способом наименьших квадратов

прежде чем указать на возможную простую реализацию процедуры оптимизации квази-Ньютона в CUDA, несколько слов о том, как работает оптимизатор квази-Ньютона.

рассмотрим функцию f of N реальные переменные x и сделайте расширение второго порядка вокруг определенной точки xi:

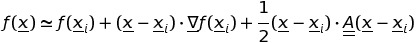
здесь A - это Гессиан матрицы.

найти минимум начиная с точки xi метод Ньютона состоит в принуждении

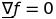
что влечет за собой

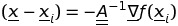
и что, в свою очередь, подразумевает знание обратной стороны Гессиана. Кроме того, для обеспечения функции уменьшается, направление обновления

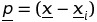
должно быть такое, что

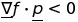
из которого следует, что

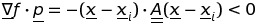
согласно вышеуказанному неравенство, матрица Гессиана должна быть определенно положительной. К сожалению, матрица Гессиана не обязательно является определенной положительной, особенно далеко от минимума f, поэтому использование обратного Гессиана, помимо вычислительной нагрузки, может быть также вредным, подталкивая процедуру еще дальше от минимума к областям возрастающих значений f. Вообще говоря, удобнее использовать метод квази-Ньютона, т. е. аппроксимацию инверсия Гессиана, которая сохраняет определенный позитив и обновляет итерацию после итераций, сходящихся к инверсии самого Гессиана. Грубое обоснование метода квази-Ньютона заключается в следующем. Считать

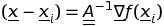
и

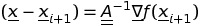
вычитая два уравнения, у нас есть правило обновления для процедуры Ньютона

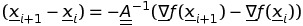
правилом обновления для процедуры квази-Ньютона является после

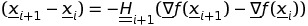
здесь Привет+1 в упомянутой матрицы, аппроксимирующей обратную мешковиной и обновление шаг за шагом.

существует несколько правил обновления Привет+1, и я не буду вдаваться в детали этого пункта. Очень распространенный из них обеспечивается Бройдена-Флетчера-Гольдфарба-Shanno, но во многих случаях Полак-Ribiére схема, достаточно эффективна.

В Реализация CUDA может следовать тем же шагам классического Численные Рецепты подходим, но с учетом этого:

1) деятельность вектора и матрицы может эффектно быть выполнена тягой CUDA или cuBLAS; 2) логика управления может быть выполнена CPU; 3) минимизация линии, включающая брекетинг корней и выводы корней, может быть выполнена на CPU, ускоряя только функциональные и градиентные оценки стоимости GPU.

выше схема, неизвестные, градиенты и Гессиан могут храниться на устройстве без необходимости перемещать их взад и вперед от хоста к устройству.

пожалуйста, обратите внимание также, что некоторые подходы доступны в литературе, в которой также предлагается попытка распараллелить минимизацию линии, см.

Y. в ФЭИ, г. Ронг, Б. Ван, В. Ван, "параллельные л-алгоритм бройдена-Б алгоритм на GPU", Компьютеры И Графика, vol. 40, 2014, с. 1-9.

В этом github страница, доступна полная реализация CUDA, обобщающая подход численных рецептов с использованием linmin, mkbrak и dbrent к параллельному случаю GPU. Этот подход реализует схему поляка-Рибьера, но может быть легко обобщен на другие задачи оптимизации квази-Ньютона.