Использование логической монады в Haskell
недавно я реализовал наивный Dpll Sat Solver на Хаскелл, адаптировано из Джона Харрисона справочник практической логики и автоматизированного рассуждения.
DPLL-это разновидность обратного поиска, поэтому я хочу поэкспериментировать с использованием логики монады С Олег Киселев и соавт. Однако я не совсем понимаю, что мне нужно изменить.
вот код, который я полученный.
- какой код мне нужно изменить, чтобы использовать логическую монаду?
- бонус: есть ли какое-либо конкретное преимущество в производительности для использования логической монады?
{-# LANGUAGE MonadComprehensions #-}
module DPLL where
import Prelude hiding (foldr)
import Control.Monad (join,mplus,mzero,guard,msum)
import Data.Set.Monad (Set, (), member, partition, toList, foldr)
import Data.Maybe (listToMaybe)
-- "Literal" propositions are either true or false
data Lit p = T p | F p deriving (Show,Ord,Eq)
neg :: Lit p -> Lit p
neg (T p) = F p
neg (F p) = T p
-- We model DPLL like a sequent calculus
-- LHS: a set of assumptions / partial model (set of literals)
-- RHS: a set of goals
data Sequent p = (Set (Lit p)) :|-: Set (Set (Lit p)) deriving Show
{- --------------------------- Goal Reduction Rules -------------------------- -}
{- "Unit Propogation" takes literal x and A :|-: B to A,x :|-: B',
- where B' has no clauses with x,
- and all instances of -x are deleted -}
unitP :: Ord p => Lit p -> Sequent p -> Sequent p
unitP x (assms :|-: clauses) = (assms' :|-: clauses')
where
assms' = (return x) `mplus` assms
clauses_ = [ c | c <- clauses, not (x `member` c) ]
clauses' = [ [ u | u <- c, u /= neg x] | c <- clauses_ ]
{- Find literals that only occur positively or negatively
- and perform unit propogation on these -}
pureRule :: Ord p => Sequent p -> Maybe (Sequent p)
pureRule sequent@(_ :|-: clauses) =
let
sign (T _) = True
sign (F _) = False
-- Partition the positive and negative formulae
(positive,negative) = partition sign (join clauses)
-- Compute the literals that are purely positive/negative
purePositive = positive (fmap neg negative)
pureNegative = negative (fmap neg positive)
pure = purePositive `mplus` pureNegative
-- Unit Propagate the pure literals
sequent' = foldr unitP sequent pure
in if (pure /= mzero) then Just sequent'
else Nothing
{- Add any singleton clauses to the assumptions
- and simplify the clauses -}
oneRule :: Ord p => Sequent p -> Maybe (Sequent p)
oneRule sequent@(_ :|-: clauses) =
do
-- Extract literals that occur alone and choose one
let singletons = join [ c | c <- clauses, isSingle c ]
x <- (listToMaybe . toList) singletons
-- Return the new simplified problem
return $ unitP x sequent
where
isSingle c = case (toList c) of { [a] -> True ; _ -> False }
{- ------------------------------ DPLL Algorithm ----------------------------- -}
dpll :: Ord p => Set (Set (Lit p)) -> Maybe (Set (Lit p))
dpll goalClauses = dpll' $ mzero :|-: goalClauses
where
dpll' sequent@(assms :|-: clauses) = do
-- Fail early if falsum is a subgoal
guard $ not (mzero `member` clauses)
case (toList . join) $ clauses of
-- Return the assumptions if there are no subgoals left
[] -> return assms
-- Otherwise try various tactics for resolving goals
x:_ -> dpll' =<< msum [ pureRule sequent
, oneRule sequent
, return $ unitP x sequent
, return $ unitP (neg x) sequent ]
2 ответов
Ok, изменение кода для использования Logic оказалось совершенно тривиальным. Я прошел и переписал все, чтобы использовать plain Set функции вместо Set монада, потому что вы на самом деле не используете Set monadically единообразно, и конечно, не отступает логика. Понимание монады также было более четко написано в виде карт, фильтров и тому подобного. Это не должно было произойти, но это помогло мне разобраться в том, что происходило, и это, безусловно, сделало очевидно, что единственная настоящая оставшаяся монада, которая использовалась для отступления, была просто Maybe.
в любом случае, вы можете просто обобщить подпись типа pureRule, oneRule и dpll работать над не просто Maybe, но ни m С ограничением MonadPlus m =>.
затем в pureRule, ваши типы не будут совпадать, потому что вы строите MaybeS явно, так что идите и измените его немного:
in if (pure /= mzero) then Just sequent'
else Nothing
становится
in if (not $ S.null pure) then return sequent' else mzero
и в oneRule, аналогично измените использование listToMaybe для явного соответствия so
x <- (listToMaybe . toList) singletons
становится
case singletons of
x:_ -> return $ unitP x sequent -- Return the new simplified problem
[] -> mzero
и, вне изменения подписи типа,dpll не нуждается в изменениях вообще!
теперь ваш код работает над и Maybe и Logic!
запустить Logic код, вы можете использовать следующую функцию:
dpllLogic s = observe $ dpll' s
можно использовать observeAll или подобное, чтобы увидеть больше результаты.
Для справки, вот полный рабочий код:
{-# LANGUAGE MonadComprehensions #-}
module DPLL where
import Prelude hiding (foldr)
import Control.Monad (join,mplus,mzero,guard,msum)
import Data.Set (Set, (\), member, partition, toList, foldr)
import qualified Data.Set as S
import Data.Maybe (listToMaybe)
import Control.Monad.Logic
-- "Literal" propositions are either true or false
data Lit p = T p | F p deriving (Show,Ord,Eq)
neg :: Lit p -> Lit p
neg (T p) = F p
neg (F p) = T p
-- We model DPLL like a sequent calculus
-- LHS: a set of assumptions / partial model (set of literals)
-- RHS: a set of goals
data Sequent p = (Set (Lit p)) :|-: Set (Set (Lit p)) --deriving Show
{- --------------------------- Goal Reduction Rules -------------------------- -}
{- "Unit Propogation" takes literal x and A :|-: B to A,x :|-: B',
- where B' has no clauses with x,
- and all instances of -x are deleted -}
unitP :: Ord p => Lit p -> Sequent p -> Sequent p
unitP x (assms :|-: clauses) = (assms' :|-: clauses')
where
assms' = S.insert x assms
clauses_ = S.filter (not . (x `member`)) clauses
clauses' = S.map (S.filter (/= neg x)) clauses_
{- Find literals that only occur positively or negatively
- and perform unit propogation on these -}
pureRule sequent@(_ :|-: clauses) =
let
sign (T _) = True
sign (F _) = False
-- Partition the positive and negative formulae
(positive,negative) = partition sign (S.unions . S.toList $ clauses)
-- Compute the literals that are purely positive/negative
purePositive = positive \ (S.map neg negative)
pureNegative = negative \ (S.map neg positive)
pure = purePositive `S.union` pureNegative
-- Unit Propagate the pure literals
sequent' = foldr unitP sequent pure
in if (not $ S.null pure) then return sequent'
else mzero
{- Add any singleton clauses to the assumptions
- and simplify the clauses -}
oneRule sequent@(_ :|-: clauses) =
do
-- Extract literals that occur alone and choose one
let singletons = concatMap toList . filter isSingle $ S.toList clauses
case singletons of
x:_ -> return $ unitP x sequent -- Return the new simplified problem
[] -> mzero
where
isSingle c = case (toList c) of { [a] -> True ; _ -> False }
{- ------------------------------ DPLL Algorithm ----------------------------- -}
dpll goalClauses = dpll' $ S.empty :|-: goalClauses
where
dpll' sequent@(assms :|-: clauses) = do
-- Fail early if falsum is a subgoal
guard $ not (S.empty `member` clauses)
case concatMap S.toList $ S.toList clauses of
-- Return the assumptions if there are no subgoals left
[] -> return assms
-- Otherwise try various tactics for resolving goals
x:_ -> dpll' =<< msum [ pureRule sequent
, oneRule sequent
, return $ unitP x sequent
, return $ unitP (neg x) sequent ]
dpllLogic s = observe $ dpll s
есть ли какое-либо конкретное преимущество в производительности для использования логической монады?
TL; DR: не то, что я могу найти, кажется, что Maybe превосходит Logic так как у него меньше накладных расходов.
я решил реализовать простой тест, чтобы проверить производительность Logic и Maybe.
В моем тесте я случайно строю 5000 CNFs с n предложения, каждое предложение, содержащее три литерала. Производительность оценивается как количество предложений n разнообразное.
в моем коде я изменил dpllLogic следующим образом:
dpllLogic s = listToMaybe $ observeMany 1 $ dpll s
я также протестировал модификации dpll С ярмарка дизъюнкция, например:
dpll goalClauses = dpll' $ S.empty :|-: goalClauses
where
dpll' sequent@(assms :|-: clauses) = do
-- Fail early if falsum is a subgoal
guard $ not (S.empty `member` clauses)
case concatMap S.toList $ S.toList clauses of
-- Return the assumptions if there are no subgoals left
[] -> return assms
-- Otherwise try various tactics for resolving goals
x:_ -> msum [ pureRule sequent
, oneRule sequent
, return $ unitP x sequent
, return $ unitP (neg x) sequent ]
>>- dpll'
затем я протестировал использование Maybe, Logic и Logic С честной дизъюнкции.
вот контрольные результаты для этого теста:
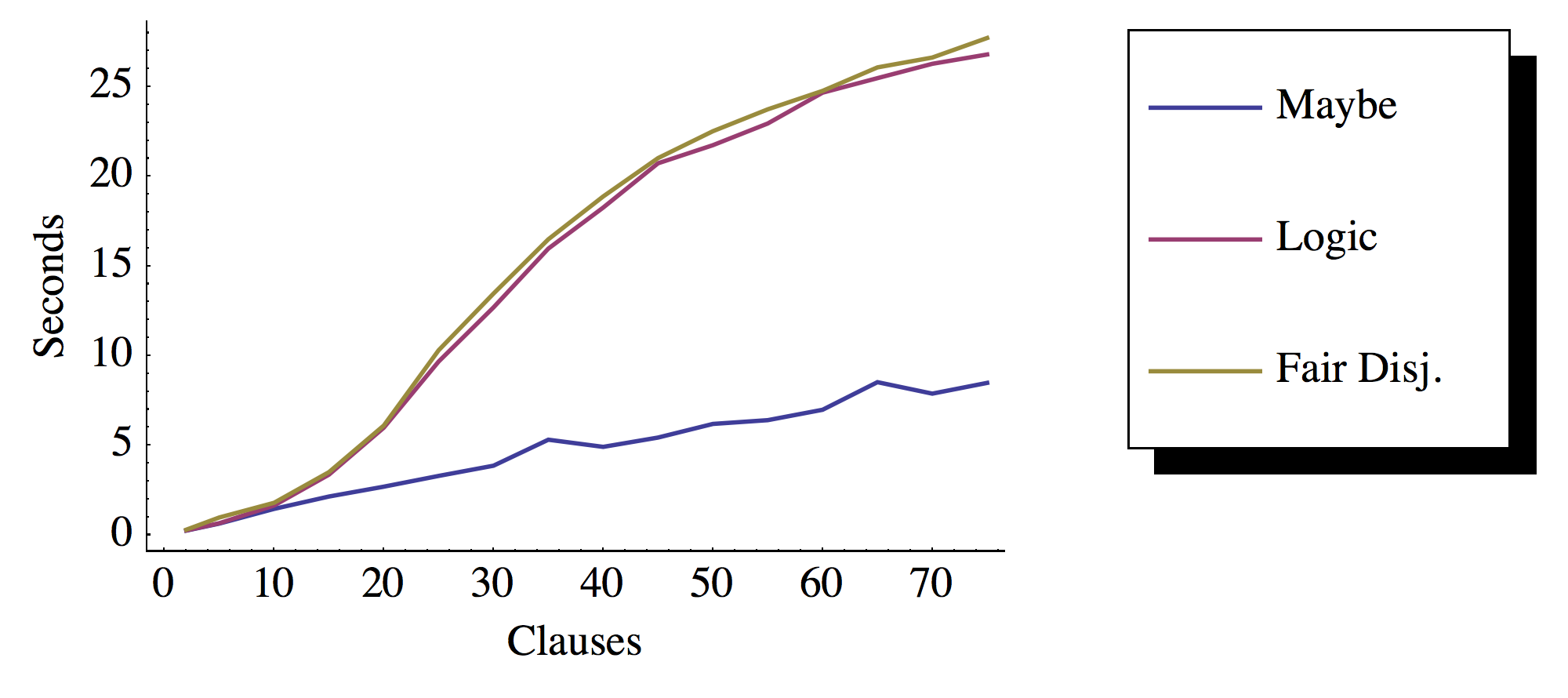
как видим,Logic С или без дизъюнкции в данном случае делает никакая разница. The dpll решить с помощью Maybe монада, похоже, работает в линейном времени в n при использовании Logic монада несет дополнительные накладные расходы. Похоже, что накладные расходы понесли плато.
здесь Main.hs файл, используемый для создания этих тестов. Кто-то, желающий воспроизвести эти критерии, может пожелать рассмотреть заметки Хаскелла о профилировании:
module Main where
import DPLL
import System.Environment (getArgs)
import System.Random
import Control.Monad (replicateM)
import Data.Set (fromList)
randLit = do let clauses = [ T p | p <- ['a'..'f'] ]
++ [ F p | p <- ['a'..'f'] ]
r <- randomRIO (0, (length clauses) - 1)
return $ clauses !! r
randClause n = fmap fromList $ replicateM n $ fmap fromList $ replicateM 3 randLit
main = do args <- getArgs
let n = read (args !! 0) :: Int
clauses <- replicateM 5000 $ randClause n
-- To use the Maybe monad
--let satisfiable = filter (/= Nothing) $ map dpll clauses
let satisfiable = filter (/= Nothing) $ map dpllLogic clauses
putStrLn $ (show $ length satisfiable) ++ " satisfiable out of "
++ (show $ length clauses)
