Использование разреженных матриц scipy для решения системы уравнений

это продолжение как настроить и решить одновременные уравнения в python но я чувствую, что заслуживает своей собственной репутации очков за любой ответ.

для фиксированного целого числа n, У меня есть набор 2(n-1) одновременные уравнения следующим образом. 

M(p) = 1+((n-p-1)/n)*M(n-1) + (2/n)*N(p-1) + ((p-1)/n)*M(p-1)

N(p) = 1+((n-p-1)/n)*M(n-1) + (p/n)*N(p-1)

M(1) = 1+((n-2)/n)*M(n-1) + (2/n)*N(0)

N(0) = 1+((n-1)/n)*M(n-1)

M(p) определен 1 <= p <= n-1. N(p) определен 0 <= p <= n-2. Заметьте также, что p - это просто постоянное целое число в каждом уравнении, поэтому вся система линейный.

некоторые очень хорошие ответы были даны для того, как настроить систему уравнений в python. Однако система разрежена, и я хотел бы решить ее для больших n. Как я могу использовать разреженное матричное представление scipy и http://docs.scipy.org/doc/scipy/reference/sparse.linalg.html например, вместо этого?

6
equations linear-algebra python scipy sparse-matrix

3 ответов

обычно я бы не стал бить мертвую лошадь, но случается, что мой не-векторизованный подход к решению вашего другого вопроса имеет некоторые достоинства, когда все становится большим. Поскольку я фактически заполнял матрицу коэффициентов по одному элементу за раз, очень легко перевести в формат разреженной матрицы COO, который можно эффективно преобразовать в CSC и решить. Это делает следующее:

import scipy.sparse

def sps_solve(n) :
    # Solution vector is [N[0], N[1], ..., N[n - 2], M[1], M[2], ..., M[n - 1]]
    n_pos = lambda p : p
    m_pos = lambda p : p + n - 2
    data = []
    row = []
    col = []
    # p = 0
    # n * N[0] + (1 - n) * M[n-1] = n
    row += [n_pos(0), n_pos(0)]
    col += [n_pos(0), m_pos(n - 1)]
    data += [n, 1 - n]
    for p in xrange(1, n - 1) :
        # n * M[p] + (1 + p - n) * M[n - 1] - 2 * N[p - 1] +
        #  (1 - p) * M[p - 1] = n
        row += [m_pos(p)] * (4 if p > 1 else 3)
        col += ([m_pos(p), m_pos(n - 1), n_pos(p - 1)] +
                ([m_pos(p - 1)] if p > 1 else []))
        data += [n, 1 + p - n , -2] + ([1 - p] if p > 1 else [])
        # n * N[p] + (1 + p -n) * M[n - 1] - p * N[p - 1] = n
        row += [n_pos(p)] * 3
        col += [n_pos(p), m_pos(n - 1), n_pos(p - 1)]
        data += [n, 1 + p - n, -p]
    if n > 2 :
        # p = n - 1
        # n * M[n - 1] - 2 * N[n - 2] + (2 - n) * M[n - 2] = n
        row += [m_pos(n-1)] * 3
        col += [m_pos(n - 1), n_pos(n - 2), m_pos(n - 2)]
        data += [n, -2, 2 - n]
    else :
        # p = 1 
        # n * M[1] - 2 * N[0] = n
        row += [m_pos(n - 1)] * 2
        col += [m_pos(n - 1), n_pos(n - 2)]
        data += [n, -2]
    coeff_mat = scipy.sparse.coo_matrix((data, (row, col))).tocsc()
    return scipy.sparse.linalg.spsolve(coeff_mat,
                                       np.ones(2 * (n - 1)) * n)

это, конечно, гораздо более многословно, чем строить его из векторизованных блоков, как Теодоросцеллеке делает, но интересная вещь происходит, когда вы время оба подхода:

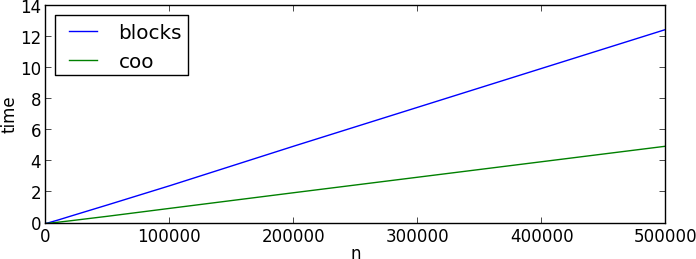
enter image description here

во-первых, и это (очень) приятно, время масштабируется линейно в обоих решениях, как можно было бы ожидать от использования разреженного подхода. Но решение, которое я дал в этом ответе, всегда быстрее, тем более для больших ns. Просто для удовольствия я также приурочил плотный подход Теодорошеллеке от другого вопроса, который дает этот хороший график, показывающий различное масштабирование обоих типов решений, и как очень рано, где-то около n = 75, решение здесь должно быть вашим выбором:

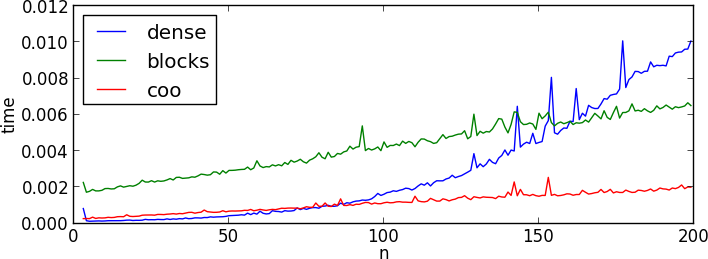
enter image description here

Я не знаю достаточно о scipy.sparse чтобы действительно выяснить, почему различия между двумя разреженными подходами, хотя я сильно подозреваю использование разреженных матриц формата LIL. Там может быть какой-то очень незначительный прирост производительности, хотя и много компактности в коде, превратив ответ Теодорошеллеке в формат COO. Но это оставлено как упражнение для операции!

5

Это решение с использованием scipy.редкий. К сожалению, проблема здесь не изложена. Поэтому, чтобы понять это решение, будущие посетители должны сначала посмотреть проблему по ссылке, указанной в вопросе.

решение с использованием scipy.редкий:

from scipy.sparse import spdiags, lil_matrix, vstack, hstack
from scipy.sparse.linalg import spsolve
import numpy as np


def solve(n):
    nrange = np.arange(n)
    diag = np.ones(n-1)

    # upper left block
    n_to_M = spdiags(-2. * diag, 0, n-1, n-1)

    # lower left block
    n_to_N = spdiags([n * diag, -nrange[-1:0:-1]], [0, 1], n-1, n-1)

    # upper right block
    m_to_M = lil_matrix(n_to_N)
    m_to_M[1:, 0] = -nrange[1:-1].reshape((n-2, 1))

    # lower right block
    m_to_N = lil_matrix((n-1, n-1))
    m_to_N[:, 0] = -nrange[1:].reshape((n-1, 1))

    # build A, combine all blocks
    coeff_mat = hstack(
                       (vstack((n_to_M, n_to_N)),
                        vstack((m_to_M, m_to_N))))

    # const vector, right side of eq.
    const = n * np.ones((2 * (n-1),1))

    return spsolve(coeff_mat.tocsr(), const).reshape((-1,1))
5

есть некоторый код, который я уже смотрел здесь:http://jkwiens.com/heat-equation-using-finite-difference/ его функция реализует метод конечных разностей для решения уравнения теплопроводности с использованием разреженного матричного пакета scipy.

0