Использование SVD для сжатия изображения в MATLAB
Я новичок в MATLAB, но пытаюсь сделать код сжатия изображений для изображений в оттенках серого.
вопросы
Как я могу использовать SVD для обрезки собственных значений с низким значением для восстановления сжатого изображения?
работа/попытки до сих пор
мой код до сих пор:
B=imread('images1.jpeg');
B=rgb2gray(B);
doubleB=double(B);
%read the image and store it as matrix B, convert the image to a grayscale
photo and convert the matrix to a class 'double' for values 0-255
[U,S,V]=svd(doubleB);
Это позволяет мне успешно разложить матрицу изображений с собственными значениями, хранящимися в переменной S.
Как я усечение S (Что такое 167x301, класс double)? Допустим, из 167 собственных значений я хочу взять только топ-100 (или любой N на самом деле), как это сделать и восстановить сжатое изображение?
обновленный код/мысли
вместо того, чтобы помещать кучу кода в раздел комментариев, это текущий проект, который у меня есть. Я смог успешно создать сжатый образ, вручную изменив N, но я хотел бы сделать 2 дополнительные вещи:
1- Покажите панель изображений для различных сжатий (i/e, запустите цикл для N = 5,10,25 и т. д.)
2 - как-то вычислить разницу (ошибку) между каждым изображением и оригиналом и график его.
я ужасен с пониманием циклов и вывода, но это то, что я пробовал:
B=imread('images1.jpeg');
B=rgb2gray(B);
doubleB=im2double(B);%
%read the image and store it as matrix B, convert the image to a grayscale
%photo and convert the image to a class 'double'
[U,S,V]=svd(doubleB);
C=S;
for N=[5,10,25,50,100]
C(N+1:end,:)=0;
C(:,N+1:end)=0;
D=U*C*V';
%Use singular value decomposition on the image doubleB, create a new matrix
%C (for Compression diagonal) and zero out all entries above N, (which in
%this case is 100). Then construct a new image, D, by using the new
%diagonal matrix C.
imshow(D);
error=C-D;
end
очевидно, есть некоторые ошибки, потому что я не получаю несколько изображений или знаю, как" график " матрицы ошибок
4 ответов
для начала, я предполагаю, что вы знаете, что SVD действительно не лучший инструмент для декорреляции пикселей в одном изображении. Но это хорошая практика.
хорошо, так мы знаем, что B = U*S*V'. И мы знаем, что S диагонально и сортируется по величине. Поэтому, используя только несколько верхних значений S, вы получите аппроксимацию своего изображения. Скажем C=U*S2*V', где S2-ваш модифицированный S. размеры U и V не изменились, поэтому самое простое, что нужно сделать сейчас, - это обнулить элементы С что вы не хотите использовать, и запустить восстановление. (Самый простой способ сделать это: S2=S; S2(N+1:end, :) = 0; S2(:, N+1:end) = 0;).
теперь для части сжатия. U и так V, поэтому независимо от того, что происходит с S2, объем данных не меняется. Но посмотрите, что происходит с U*S2. (Построить изображение). Если вы сохранили N сингулярных значений в S2, тогда только первые n строк S2 отличны от нуля. Сжатие! Кроме того, вам все еще приходится иметь дело с V. Вы не можете использовать то же самое трюк после того, как вы уже сделали (U*S2), так как больше U*S2 не равно нулю, чем S2 был сам по себе. Как мы можем использовать S2 с обеих сторон? Ну, это диагональ, так что используйте D=sqrt(S2), а теперь C=U*D*D*V'. Так что теперь U*D имеет только N ненулевых строк и D*V' имеет только N ненулевых столбцов. Передайте только эти величины, и вы сможете реконструировать C, который примерно как B.
хотя этот вопрос старый, он очень помог мне понять SVD. Я изменил код, который вы написали в своем вопросе, чтобы он работал.
Я считаю, что вы, возможно, решили проблему, однако только для будущей справки для тех, кто посещает эту страницу, Я включаю полный код здесь с выходными изображениями и графиком.
ниже код:
close all
clear all
clc
%reading and converting the image
inImage=imread('fruits.jpg');
inImage=rgb2gray(inImage);
inImageD=double(inImage);
% decomposing the image using singular value decomposition
[U,S,V]=svd(inImageD);
% Using different number of singular values (diagonal of S) to compress and
% reconstruct the image
dispEr = [];
numSVals = [];
for N=5:25:300
% store the singular values in a temporary var
C = S;
% discard the diagonal values not required for compression
C(N+1:end,:)=0;
C(:,N+1:end)=0;
% Construct an Image using the selected singular values
D=U*C*V';
% display and compute error
figure;
buffer = sprintf('Image output using %d singular values', N)
imshow(uint8(D));
title(buffer);
error=sum(sum((inImageD-D).^2));
% store vals for display
dispEr = [dispEr; error];
numSVals = [numSVals; N];
end
% dislay the error graph
figure;
title('Error in compression');
plot(numSVals, dispEr);
grid on
xlabel('Number of Singular Values used');
ylabel('Error between compress and original image');
применение этого к следующему изображению:

дает следующий результат только с первыми 5 сингулярными значениями,

С первыми 30 сингулярными значениями,

и первые 55 сингулярных значений,

изменение ошибки с увеличением числа сингулярных значений можно увидеть на графике ниже.
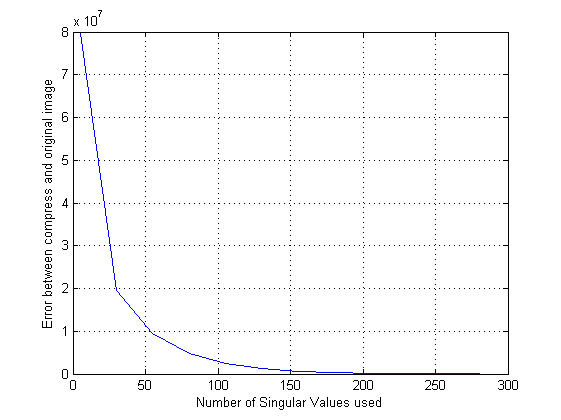
здесь вы можете заметить, что график показывает, что использование приблизительно 200 первых сингулярных значений дает приблизительно нулевая ошибка.
например, вот изображение 512 x 512 B&W Лена:
мы вычисляем SVD Лены. Выбирая сингулярные значения выше 1% от максимального сингулярного значения, мы остаемся только с 53 сингулярные значения. Восстанавливая Лену с этими сингулярными значениями и соответствующими (левыми и правыми) сингулярными векторами, получаем приближение низкого ранга of Лена:
вместо хранения 512 * 512 = 262144 значений (каждый из которых принимает 8 бит), мы можем хранить 2 x (512 x 53) + 53 = 54325 значений, что приблизительно 20% от исходного размера. Это один из примеров того, как SVD можно использовать для сжатия изображений с потерями.
здесь MATLAB код:
% open Lena image and convert from uint8 to double
Lena = double(imread('LenaBW.bmp'));
% perform SVD on Lena
[U,S,V] = svd(Lena);
% extract singular values
singvals = diag(S);
% find out where to truncate the U, S, V matrices
indices = find(singvals >= 0.01 * singvals(1));
% reduce SVD matrices
U_red = U(:,indices);
S_red = S(indices,indices);
V_red = V(:,indices);
% construct low-rank approximation of Lena
Lena_red = U_red * S_red * V_red';
% print results to command window
r = num2str(length(indices));
m = num2str(length(singvals));
disp(['Low-rank approximation used ',r,' of ',m,' singular values']);
% save reduced Lena
imwrite(uint8(Lena_red),'Reduced Lena.bmp');
взятие первого N максимального числа собственных значений и соответствующих им собственных векторов может решить вашу проблему.Для PCA исходные данные, умноженные на первые восходящие собственные векторы, построят ваше изображение на n x d, где d представляет количество собственных векторов.


