java-объединить adiacent прямоугольники в многоугольник
У меня есть набор прямоугольников, которые имеют одинаковую ширину и высоту и всегда идиакант. Я знаю положение всех вершин, каждая из которых имеет только 4. (потому что это квадрат).
Это изображение может объяснить это: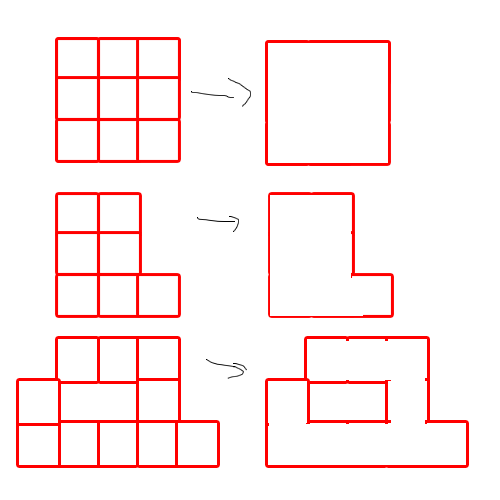
Если есть какие-либо пробелы, это нормально, если алгоритм заполнения пробелов.
Я много искал и не мог найти ничего хорошего.. Мне нужен простой алгоритм, он не должен быть эффективным.. Допустим, у нас 7 прямоугольников как и во втором примере полигона изображения. Хорошо, если я сначала объединю 1 с 2, затем объединю наш новый многоугольник с 3 и так далее, это не должно быть так быстро, потому что будет максимум 50 прямоугольников.
2 ответов
мне очень нравится эффективность ответа Дариуша. И может быть, он отвечает всем вашим требованиям, и в этом случае идите с ним.
однако, есть несколько проблем, которые приходят на ум.
что делать, если после слияния есть несколько фигур? Как вы можете определить, являются ли эти фигуры отдельными или вложенными? В этом случае, если вам просто дан набор ребер, нелегко сказать, составляет ли он форму или пустоту, оставленную внутри форма.
например, рассмотрим следующую диаграмму после объединения соседних квадратов:
+----------------+
| |
| +------------+ |
| | | |
| | +--------+ | |
| | | | | |
| | | | | |
| | +--------+ | |
| | | |
| +------------+ |
| |
+----------------+
здесь действительно 2 формы - 1 внутри другого. Однако, 3 набора Соединенных краев. Чтобы увидеть, является ли внутренний прямоугольник фигурой или пустотой внутри фигуры, вы должны начать с внешнего прямоугольника и работать внутрь. Это приведет к тому, что форма будет в основном контуром прямоугольника, окружающего другой прямоугольник. Если бы ты ... удалите внешние края, однако, полученная форма будет просто полый прямоугольник - одна форма.
предполагая, что это имеет отношение к вашей проблеме (это может быть не так), то следующий алгоритм может быть более подходящим:
вместо того, чтобы бросать набор всех ребер всех прямоугольников вместе в начале, держите каждый прямоугольник отдельно в списке Polygons. Каждый Polygon имеет свой собственный набор ребер.
слияние Polygons в этом списке, которые разделяют край, пока вы не останетесь с набором distinct Polygons (т. е. больше не может происходить слияния).
List<Polygon> plist;
// Populate the list with the polygons...
for (int i=0; i<plist.size(); i++) {
Polygon p1 = plist.get(i);
boolean distinct = false;
while (!distinct) {
distinct = true;
for (int j=plist.size()-1 ; j>i; j--) {
Polygon p2 = plist.get(j);
if (p1.sharesEdge(p2)) {
// Merge the two polygons
p1.merge(p2);
// One less shape
plist.remove(j);
distinct = false;
} // if (p1.sharesEdge(p2))
} // for (int j=plist.size()-1 ; j>i; j--)
} // while (!distinct)
} // for (int i=0; i<plist.size(); i++)
в конце у вас будет список отдельных Polygons в plist.
sharesEdge просто петли по краям каждого Polygon и видит, есть ли у них что-то общее.
merge делает точно так же, как ответ Дариуша - удаляет пары ребер.
некоторые предположения - все начальные полигоны имеют ребра единичной длины. Если это не true, тогда вам может потребоваться разделить ребра при слиянии и иметь более сложный метод проверки общих ребер.
если вложенные фигуры необходимо обрабатывать, поглощая их в большую форму (т. е. заполнить пробелы), тогда это становится немного сложнее. Вы бы начали с создания контура ребер. Если все ребра соединены, то это простая форма, где ее ребра определяют периметр. Если нет, то должен быть один внешний периметр, и один или больше внутренних периметров. Игнорируйте внутренние периметры и разрешите форму к простому - т. е. сохраняются только края во внешнем периметре. Затем сделайте петлю над фигурами и посмотрите, находится ли какая-либо из фигур внутри другой. Если это так, удалите его.
поскольку ваша форма состоит только из прямоугольников, и они всегда смежны, алгоритм слияние гораздо проще, чем было бы без этих предположений.
- Создайте список всех ребер из ваших прямоугольников. Один прямоугольник имеет 4 ребра.
- пусть
Edgeбыть классом с правильно определеннымиcompareTo()иequals(). - сортировка списка ребер (использует
compareTo). - повторите список. Если же края присутствуя в списке дважды, удалите их обоих из списка.
- оставшиеся ребра по краям полигона.
