Как быстро определить, делится ли" неизвестное " число на 3?

любые три последовательных числа суммируются до 0 == a + a + 1 + a + 2 mod 3. Ответ сводится к k%3 == 0, или 2k-1% 3 == 0. Последнее эквивалентно k%3 == 2, что исключает k%3==1, что упрощает далее до k%3 != 1.

это известный трюк в математике, что число делится на три, если сумма его отдельных десятичных цифр делится на три.

пример:

2271

2+2+7+1 = 12

12 is divisible by 3, therefore so is 2271

кроме того, сумма любых трех последовательных целых чисел должно быть кратно трем. Это потому, что:

((n)+(n+1)+(n+2))/3 = (3n+3)/3 = n+1 = integer

таким образом:

если k mod 3 == 0, затем конкатенация от 1 до k делится на три.

если k mod 3 == 1, затем конкатенация от 1 до k не делится на три.

если k mod 3 == 2, тогда это немного сложнее. В этом случае конкатенация от 1 до k делится на три, если сумма k и номер перед k (который оценивает в (k)+(k-1), которая составляет 2k-1) делится на три.

таким образом, окончательное условие:

(k mod 3 == 0) || ((k mod 3 == 2) && (2k-1 mod 3 == 0))

тем не менее, это может быть еще более упрощено.

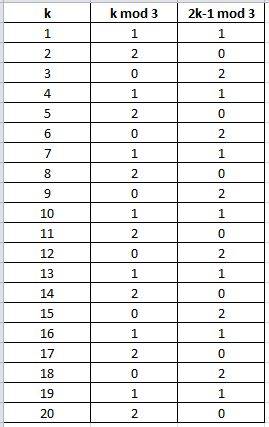
получается, что k mod 3 может только равный 2 всякий раз, когда 2k-1 mod 3 равна 0 и наоборот.

см. график ниже, который показывает циклический образец такого поведения.

таким образом, формула может быть упрощена просто:

(k mod 3 == 0) || (k mod 3 == 2) 

или, еще проще:

(k mod 3 != 1)

Я понимаю, что ответчик уже предоставил этот ответ, поэтому я не ожидаю, что это будет принятый ответ, просто давая более тщательный математический объяснение.

число делится на три, если сумма его цифр делится на три (см. здесь). Поэтому нет необходимости "строить" свой номер, вам нужно просто добавить цифры отдельных номеров. Таким образом, для вашего случая 15 Вам не нужно "строить" 123456789101112131415, вам просто нужно суммировать все цифры в [1, 2, 3, 4, ... 14, 15].

Это проще, чем кажется, потому что проблему должен только проверить номера в формате: 12345789101112131415...k. Вы можете использовать метод Гаусса, чтобы быстро получить сумму чисел от 1 до k, а затем проверить, делится ли эта сумма на три, используя обычные методы. Этот код:

'NO' if (k*(k+1)/2)%3 else 'YES'

если вы посмотрите на шаблон, который возникает при увеличении k (НЕТ, ДА, ДА, НЕТ, ДА, ДА,...), вам даже не нужно умножение или деление. В короче, все, что вам нужно, это:

'YES' if (k-1)%3 else 'NO'

вот код Python, который читает целые числа из файла, и, если это не займет слишком много времени, также проверяет ответ на жесткий путь, чтобы вы могли видеть, что это правильно. (Числа Python могут быть бесконечно длинными, поэтому вам не нужно беспокоиться о переполнении):

#!/usr/bin/python3
# Read integers from stdin, convert each int to a triangular number
# and output YES (or NO) if it is divisible by 3.

def sumgauss(x):
    '''Return the sum from 1 to x using Gauss's shortcut'''
    return (x*(x+1)/2)

def triangle(n):
    '''Given an integer n, return a string with all the integers 
       from 1 to n concatenated. E.g., 15 -> 123456789101112131415'''
    result=""
    for t in range(1, k+1):
        result+=str(t)
    return result

import sys
for k in sys.stdin.readlines():
    k=int(k)
    print ( 'YES' if (k-1)%3 else 'NO', end='')

    # If it wouldn't take too long, double check by trying it the hard way
    if k<100000:
        kstr=triangle(k)
        print("\t// %s modulo 3 is %d" % (kstr, int(kstr)%3))
    else:
        print('\t// 123456789101112131415...%d%d%d modulo 3 is %d' %
              tuple([k-2, k-1, k, sumgauss(k)%3]))

говоря о ярлыке Гаусса для суммирования, эта проблема очень похожа на домашнее задание. (Гаусс изобрел его в качестве студента, когда учитель пытался вытащить класс из его волосы на некоторое время, заставляя их складывать числа от 1 до 100.) Если это действительно классное задание, пожалуйста, убедитесь, что учитель знает, чтобы дать A мне и stackoverflow. Спасибо!

пример вывода:

$ cat data
2
6
15
130000000
130000001

$ ./k3.py < data
YES // 12 modulo 3 is 0
YES // 123456 modulo 3 is 0
YES // 123456789101112131415 modulo 3 is 0
NO  // 123456789101112131415...129999998129999999130000000 modulo 3 is 1
YES // 123456789101112131415...129999999130000000130000001 modulo 3 is 0

первые 32 Треугольных чисел:

$ seq 32 | ./k3.py
NO  // 1 modulo 3 is 1
YES // 12 modulo 3 is 0
YES // 123 modulo 3 is 0
NO  // 1234 modulo 3 is 1
YES // 12345 modulo 3 is 0
YES // 123456 modulo 3 is 0
NO  // 1234567 modulo 3 is 1
YES // 12345678 modulo 3 is 0
YES // 123456789 modulo 3 is 0
NO  // 12345678910 modulo 3 is 1
YES // 1234567891011 modulo 3 is 0
YES // 123456789101112 modulo 3 is 0
NO  // 12345678910111213 modulo 3 is 1
YES // 1234567891011121314 modulo 3 is 0
YES // 123456789101112131415 modulo 3 is 0
NO  // 12345678910111213141516 modulo 3 is 1
YES // 1234567891011121314151617 modulo 3 is 0
YES // 123456789101112131415161718 modulo 3 is 0
NO  // 12345678910111213141516171819 modulo 3 is 1
YES // 1234567891011121314151617181920 modulo 3 is 0
YES // 123456789101112131415161718192021 modulo 3 is 0
NO  // 12345678910111213141516171819202122 modulo 3 is 1
YES // 1234567891011121314151617181920212223 modulo 3 is 0
YES // 123456789101112131415161718192021222324 modulo 3 is 0
NO  // 12345678910111213141516171819202122232425 modulo 3 is 1
YES // 1234567891011121314151617181920212223242526 modulo 3 is 0
YES // 123456789101112131415161718192021222324252627 modulo 3 is 0
NO  // 12345678910111213141516171819202122232425262728 modulo 3 is 1
YES // 1234567891011121314151617181920212223242526272829 modulo 3 is 0
YES // 123456789101112131415161718192021222324252627282930 modulo 3 is 0
NO  // 12345678910111213141516171819202122232425262728293031 modulo 3 is 1
YES // 1234567891011121314151617181920212223242526272829303132 modulo 3 is 0 

вы можете доказать, что если N или N-2 делится на 3, то сумма до n делится на 3 (например, в вашем случае сумма(1...8), sum (1..9), sum (1..11) и т. д.).