Как эффективно определить, является ли многоугольник выпуклым, невыпуклым или сложным?

вы можете сделать вещи намного проще, чем алгоритм подарочной упаковки... это хороший ответ, когда у вас есть набор точек без какой-либо конкретной границы, и нужно найти выпуклую оболочку.

напротив, рассмотрим случай, когда многоугольник не является самопересекающимся и состоит из набора точек в списке, где последовательные точки образуют границу. В этом случае гораздо проще выяснить, является ли многоугольник выпуклым или нет (и вам не нужно вычислять какие-либо углы, либо):

для каждой последовательной пары ребер многоугольника (каждого триплета точек) вычислите z-компонент поперечного произведения векторов, определенных ребрами, указывающими на точки в порядке возрастания. Взять векторное произведение этих векторов:

 given p[k], p[k+1], p[k+2] each with coordinates x, y:
 dx1 = x[k+1]-x[k]
 dy1 = y[k+1]-y[k]
 dx2 = x[k+2]-x[k+1]
 dy2 = y[k+2]-y[k+1]
 zcrossproduct = dx1*dy2 - dy1*dx2

многоугольник выпукл, если z-компоненты поперечных произведений либо все положительные, либо все отрицательные. В противном случае многоугольник называется невыпуклым.

Если есть N точек, убедитесь, что вы вычисляете N перекрестных произведений, например, обязательно используйте триплеты (p[N-2],p[N-1],p[0]) и (p[N-1],p[0],p[1]).

если многоугольник является самопересекающимся, то это не соответствует техническому определению выпуклости даже если его направленные углы находятся в одном направлении, в этом случае вышеуказанный подход не даст правильного результата.

следующая функция/метод Java является реализацией алгоритма, описанного в ответ.

public boolean isConvex()
{
    if (_vertices.size() < 4)
        return true;

    boolean sign = false;
    int n = _vertices.size();

    for(int i = 0; i < n; i++)
    {
        double dx1 = _vertices.get((i + 2) % n).X - _vertices.get((i + 1) % n).X;
        double dy1 = _vertices.get((i + 2) % n).Y - _vertices.get((i + 1) % n).Y;
        double dx2 = _vertices.get(i).X - _vertices.get((i + 1) % n).X;
        double dy2 = _vertices.get(i).Y - _vertices.get((i + 1) % n).Y;
        double zcrossproduct = dx1 * dy2 - dy1 * dx2;

        if (i == 0)
            sign = zcrossproduct > 0;
        else if (sign != (zcrossproduct > 0))
            return false;
    }

    return true;
}

алгоритм гарантированно работает до тех пор, пока вершины упорядочены (по часовой стрелке или против часовой стрелки), и у вас нет самопересекающихся ребер (т. е. он работает только для простые многоугольники).

этот вопрос теперь является первым элементом в Bing или Google при поиске "определить выпуклый многоугольник.- Однако ни один из ответов недостаточно хорош.

The принятый ответ от @EugeneYokota работает, проверяя, можно ли сделать неупорядоченный набор точек выпуклым многоугольником, но это не то, что просил OP. Он попросил способ проверить, является ли данный многоугольник выпуклым или нет. ("Многоугольник" в информатике обычно определено [как в документация XFillPolygon] как упорядоченный массив 2D точек, с последовательными точками, Соединенными со стороной, а также последней точкой к первой.) Кроме того, алгоритм подарочной упаковки в этом случае будет иметь временную сложность O(n^2) на n points-что намного больше, чем необходимо для решения этой проблемы, в то время как вопрос требует эффективного алгоритма.

ответ @ JasonS вместе с другие ответы, которые следуют его идее, принимает звездчатых многоугольников например,пентаграмма или в комментарии @zenna, но звездные полигоны не считаются выпуклыми. Как @plasmacel отмечает в комментарии, это хороший подход для использования, если у вас есть предварительные знания о том, что многоугольник не является самопересекающимся, но он может потерпеть неудачу, если у вас нет этих знаний.

@Sekhat это!--10--> - это правильно, но он также имеет время-сложность O(n^2) и, таким образом, является неэффективным.

@ LorenPechtel добавил ответ после ее редактирования лучше всего здесь, но это неопределенно.

правильный алгоритм с оптимальной сложностью

алгоритм, который я здесь представляю, имеет временную сложность O(n), правильно проверяет, является ли многоугольник выпуклым или нет, и проходит все тесты, которые я бросил на него. Идея заключается в Траверс сторон многоугольника, отмечая направление каждой стороны и подписанное изменение направления между последовательными сторонами. "Подписано" здесь означает, что левый-положительный, а правый-отрицательный (или наоборот), а прямой-ноль. Эти углы нормируются, чтобы быть между минус-pi (эксклюзив) и pi (включительно). резюме все эти углы изменения направления (a.к. a прогиб углы) вместе приведет к плюс-или-минус один ход (т. е. 360 Градусы) для выпуклого многоугольника, в то время как звездообразный многоугольник (или самопересекающаяся петля) будет иметь другую сумму ( n * 360 градусов, для n повороты в целом, для полигонов, где все углы отклонения имеют один и тот же знак). Поэтому мы должны проверить, что сумма углов изменения направления равна плюс-минус одному повороту. Мы также проверяем, что углы изменения направления все положительные или все отрицательные и не обратные (радианы pi), все точки являются фактическими 2D точками, и что последовательные вершины не идентичны. (Этот последний момент спорен-вы можете разрешить повторные вершины,но я предпочитаю запретить их.) Комбинация этих проверок захватывает все выпуклые и невыпуклые многоугольники.

вот код для Python 3, который реализует алгоритм и включает в себя некоторые незначительные эффективности. Код выглядит длиннее, чем на самом деле, из-за строк комментариев и бухгалтерии, участвующих во избежание повторных точечных обращений.

TWO_PI = 2 * pi

def is_convex_polygon(polygon):
    """Return True if the polynomial defined by the sequence of 2D
    points is 'strictly convex': points are valid, side lengths non-
    zero, interior angles are strictly between zero and a straight
    angle, and the polygon does not intersect itself.

    NOTES:  1.  Algorithm: the signed changes of the direction angles
                from one side to the next side must be all positive or
                all negative, and their sum must equal plus-or-minus
                one full turn (2 pi radians). Also check for too few,
                invalid, or repeated points.
            2.  No check is explicitly done for zero internal angles
                (180 degree direction-change angle) as this is covered
                in other ways, including the `n < 3` check.
    """
    try:  # needed for any bad points or direction changes
        # Check for too few points
        if len(polygon) < 3:
            return False
        # Get starting information
        old_x, old_y = polygon[-2]
        new_x, new_y = polygon[-1]
        new_direction = atan2(new_y - old_y, new_x - old_x)
        angle_sum = 0.0
        # Check each point (the side ending there, its angle) and accum. angles
        for ndx, newpoint in enumerate(polygon):
            # Update point coordinates and side directions, check side length
            old_x, old_y, old_direction = new_x, new_y, new_direction
            new_x, new_y = newpoint
            new_direction = atan2(new_y - old_y, new_x - old_x)
            if old_x == new_x and old_y == new_y:
                return False  # repeated consecutive points
            # Calculate & check the normalized direction-change angle
            angle = new_direction - old_direction
            if angle <= -pi:
                angle += TWO_PI  # make it in half-open interval (-Pi, Pi]
            elif angle > pi:
                angle -= TWO_PI
            if ndx == 0:  # if first time through loop, initialize orientation
                if angle == 0.0:
                    return False
                orientation = 1.0 if angle > 0.0 else -1.0
            else:  # if other time through loop, check orientation is stable
                if orientation * angle <= 0.0:  # not both pos. or both neg.
                    return False
            # Accumulate the direction-change angle
            angle_sum += angle
        # Check that the total number of full turns is plus-or-minus 1
        return abs(round(angle_sum / TWO_PI)) == 1
    except (ArithmeticError, TypeError, ValueError):
        return False  # any exception means not a proper convex polygon

чтобы проверить выпуклость многоугольника, каждая точка многоугольника должна быть на уровне или за каждой линией.

вот пример картинки:

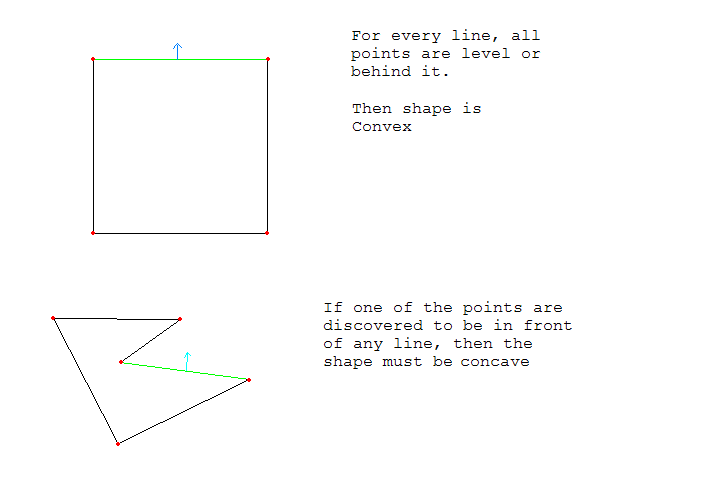
вот тест, чтобы проверить, является ли многоугольник выпуклой.

рассмотрим каждый набор из трех точек вдоль многоугольника. Если каждый угол равен 180 градусам или меньше, у вас есть выпуклый многоугольник. Когда вы вычисляете каждый угол, также держите идущую сумму (180-angle). Для выпуклого многоугольника это составит 360.

этот тест выполняется в O (n) времени.

также учтите, что в большинстве случаев этот расчет можно сделать один раз и сохранить большую часть времени у вас есть набор полигонов для работы, которые не меняются все время.

на ответ @RoryDaulton мне кажется лучшим, но что, если один из углов точно равен 0? Некоторые могут захотеть, чтобы такой крайний случай вернул True, и в этом случае измените "

if orientation * angle < 0.0:  # not both pos. or both neg.

вот мои тестовые примеры, которые подчеркивают проблему:

# A square    
assert is_convex_polygon( ((0,0), (1,0), (1,1), (0,1)) )

# This LOOKS like a square, but it has an extra point on one of the edges.
assert is_convex_polygon( ((0,0), (0.5,0), (1,0), (1,1), (0,1)) )

2-й assert терпит неудачу в исходном ответе. А должно? Для моего случая использования я бы предпочел этого не делать.

я реализовал оба алгоритма: один, опубликованный @UriGoren (с небольшим улучшением - только целочисленная математика) и один из @RoryDaulton, в Java. У меня были некоторые проблемы, потому что мой многоугольник закрыт, поэтому оба алгоритма рассматривали второй как вогнутый, когда он был выпуклым. Поэтому я изменил его, чтобы предотвратить такую ситуацию. Мои методы также используют базовый индекс (который может быть или не быть 0).

Это мои тестовые вершины:

// concave
int []x = {0,100,200,200,100,0,0};
int []y = {50,0,50,200,50,200,50};

// convex
int []x = {0,100,200,100,0,0};
int []y = {50,0,50,200,200,50};

и теперь алгоритмы:

private boolean isConvex1(int[] x, int[] y, int base, int n) // Rory Daulton
{
  final double TWO_PI = 2 * Math.PI;

  // points is 'strictly convex': points are valid, side lengths non-zero, interior angles are strictly between zero and a straight
  // angle, and the polygon does not intersect itself.
  // NOTES:  1.  Algorithm: the signed changes of the direction angles from one side to the next side must be all positive or
  // all negative, and their sum must equal plus-or-minus one full turn (2 pi radians). Also check for too few,
  // invalid, or repeated points.
  //      2.  No check is explicitly done for zero internal angles(180 degree direction-change angle) as this is covered
  // in other ways, including the `n < 3` check.

  // needed for any bad points or direction changes
  // Check for too few points
  if (n <= 3) return true;
  if (x[base] == x[n-1] && y[base] == y[n-1]) // if its a closed polygon, ignore last vertex
     n--;
  // Get starting information
  int old_x = x[n-2], old_y = y[n-2];
  int new_x = x[n-1], new_y = y[n-1];
  double new_direction = Math.atan2(new_y - old_y, new_x - old_x), old_direction;
  double angle_sum = 0.0, orientation=0;
  // Check each point (the side ending there, its angle) and accum. angles for ndx, newpoint in enumerate(polygon):
  for (int i = 0; i < n; i++)
  {
     // Update point coordinates and side directions, check side length
     old_x = new_x; old_y = new_y; old_direction = new_direction;
     int p = base++;
     new_x = x[p]; new_y = y[p];
     new_direction = Math.atan2(new_y - old_y, new_x - old_x);
     if (old_x == new_x && old_y == new_y)
        return false; // repeated consecutive points
     // Calculate & check the normalized direction-change angle
     double angle = new_direction - old_direction;
     if (angle <= -Math.PI)
        angle += TWO_PI;  // make it in half-open interval (-Pi, Pi]
     else if (angle > Math.PI)
        angle -= TWO_PI;
     if (i == 0)  // if first time through loop, initialize orientation
     {
        if (angle == 0.0) return false;
        orientation = angle > 0 ? 1 : -1;
     }
     else  // if other time through loop, check orientation is stable
     if (orientation * angle <= 0)  // not both pos. or both neg.
        return false;
     // Accumulate the direction-change angle
     angle_sum += angle;
     // Check that the total number of full turns is plus-or-minus 1
  }
  return Math.abs(Math.round(angle_sum / TWO_PI)) == 1;
}

а теперь от Ури Горена

private boolean isConvex2(int[] x, int[] y, int base, int n)
{
  if (n < 4)
     return true;
  boolean sign = false;
  if (x[base] == x[n-1] && y[base] == y[n-1]) // if its a closed polygon, ignore last vertex
     n--;
  for(int p=0; p < n; p++)
  {
     int i = base++;
     int i1 = i+1; if (i1 >= n) i1 = base + i1-n;
     int i2 = i+2; if (i2 >= n) i2 = base + i2-n;
     int dx1 = x[i1] - x[i];
     int dy1 = y[i1] - y[i];
     int dx2 = x[i2] - x[i1];
     int dy2 = y[i2] - y[i1];
     int crossproduct = dx1*dy2 - dy1*dx2;
     if (i == base)
        sign = crossproduct > 0;
     else
     if (sign != (crossproduct > 0))
        return false;
  }
  return true;
}

этот метод будет работать на простых полигонах (без самопересекающихся ребер), предполагая, что вершины упорядочены (по часовой стрелке или против)

для массива вершин:

vertices = [(0,0),(1,0),(1,1),(0,1)]

следующее python реализация проверяет, является ли z компонент всех перекрестных продуктов имеет такой же знак

def zCrossProduct(a,b,c):
   return (a[0]-b[0])*(b[1]-c[1])-(a[1]-b[1])*(b[0]-c[0])

def isConvex(vertices):
    if len(vertices)<4:
        return True
    signs= [zCrossProduct(a,b,c)>0 for a,b,c in zip(vertices[2:],vertices[1:],vertices)]
    return all(signs) or not any(signs)

адаптированный код Uri в matlab. Надеюсь, это поможет.

имейте в виду, что алгоритм Uri работает только для простые многоугольники! Итак, не забудьте сначала проверить, прост ли многоугольник!

% M [ x1 x2 x3 ...
%     y1 y2 y3 ...]
% test if a polygon is convex

function ret = isConvex(M)
    N = size(M,2);
    if (N<4)
        ret = 1;
        return;
    end

    x0 = M(1, 1:end);
    x1 = [x0(2:end), x0(1)];
    x2 = [x0(3:end), x0(1:2)];
    y0 = M(2, 1:end);
    y1 = [y0(2:end), y0(1)];
    y2 = [y0(3:end), y0(1:2)];
    dx1 = x2 - x1;
    dy1 = y2 - y1;
    dx2 = x0 - x1;
    dy2 = y0 - y1;
    zcrossproduct = dx1 .* dy2 - dy1 .* dx2;

    % equality allows two consecutive edges to be parallel
    t1 = sum(zcrossproduct >= 0);  
    t2 = sum(zcrossproduct <= 0);  
    ret = t1 == N || t2 == N;

end